牛客网 剑指offer刷题 小总结
牛客网剑指offer
刷了一些题,现在我们来总结输出一下!
挑拣我觉得自己还不够的题目
字符串
正则表达式
// ? 0个或1个 * 0个或多个 + 一个或多个
// \\d 数字 注意这个,不是\d,前面还要再加\
// (?:\\.\\d*)? (?: )? 可匹配可不匹配部分
String str, pattern;
str.matches(pattern);
pattern = "^[-\\+]?\\d*(?:\\.\\d*)?(?:[eE][+-]?\\d+)?$"
// char[] 转 String
new String(char[])
字符流中第一个不重复的字符
额外申请一个字符为下标的计次数组,按字节流顺序检索数据,出现一次的字符则为结果。
字符串转整型,不能用库函数
要点:
- 判断符号
- 每一位拿下来
- 乘之前判断是否会溢出,另外,个位上,正数最大为7,负数最大为8
- 最后别忘记负数添负号
数组
求数组中的逆序对
把这个问题演变成归并排序,分开的前部比后部大,那么这两个数字即组成了逆序对
把数组排成最小的数
实际就是比较s1+s2 和s2+s1的大小进行排序
int可以用加号加上“”进行连接
numbers[j]+""+numbers[i]但是需要比较大小还是需要在通过valueOf转型。字符串不能比较大小
数组中出现次数超过一般的数字
简单想的用HashMap即可,统计次数
或者两队人抵消的思维:先进一队兵,只要非我,就会造成战斗减员,始终能在场中留兵,说明个数大于一般。但是要校验特殊情况,即两方人数一致,战到最后,被第三方截胡,所以最后得到的结果要再次回带检验查看次数
链表
从尾到头打印链表
倒置即想到栈,也可以用头插法新建一个list,都能达到倒置的结果。
链表中环的入口节点
思维题,采用双指针,这种题画图分析获得思路
删除链表中重复的节点
当时做,指针关系弄得很乱。
因为要将重复节点全部删除,所以必须要留前置指针。主意好分情况讨论!
public ListNode deleteDuplication(ListNode pHead)
{
ListNode Head = new ListNode(0);
Head.next = pHead;
ListNode pre = Head;
ListNode p = pHead;
while(p != null){
if(p.next != null && p.next.val==p.val){
while(p.next != null && p.next.val == p.val) p = p.next;
p = p.next;
pre.next = p;
}else{
// 针对非连续序列,之前是连着的,pre过来到p这即可
pre = p;
p = p.next;
}
}
return Head.next;
}
链表中倒数第k个节点
双指针解决,前指针提前出发,领先后指针 k个身位,那么,前指针指到最后时,后指针则为倒数第k个结点。
两个链表的第一个公共结点
如果两个链表有公共结点,那么A走完再从B走,B走完再从A走,终究会碰到
树
重建二叉树
根据前序和中序序列进行重建。在前序序列中走,在中序中找到对应位置,前部分是左子树,后部分是右子树。着重点是怎么划分数组
if(in[i]==pre[pre_start]){
r.left = recurrentConstruct(pre, pre_start+1, pre_start + i - in_start, in, in_start, i-1);
r.right = recurrentConstruct(pre, pre_start + i - in_start + 1, pre_end, in, i+1, in_end);
}
比如属于left子树的前序数组停在哪里? pre_start+1开始,中序序列,从in_start到i-1是i-1-in_start个所以,前序停在,pre_start + 1 + i - 1 - in_start所以,为pre_start+i-in_start。其余类似。
二叉树的下一个节点
给一个树节点求中序遍历顺序的下一个节点,提供指父节点的指针。
除了求根,然后遍历求
多画图,还可以分析二叉树中序遍历的规律。
-
有右子树, 找子树最左节点
-
无右子树,且是父的左子树,则父节点就是下一个
-
无右子树,且是父的右子树,则一直向上找到是父的左为止,返回父 三种情况。这样快,但是注意书写,不要写错
对称的二叉树
实际上就是看每个节点的左右节点情况:
- 都为空,返回true
- 其一为空,返回false
- 若左值等于右值,继续递归左树的左和右树的右,左树的右和右树的左。不等则为false
之字顺序打印二叉树
层次遍历的变种,注意偶数层倒置即可,倒置,头插法建立list,考虑一下?
二叉搜索树第k小的节点
二叉搜索树中序遍历即是升序遍历,易找第k小
求二叉树的镜像
前序递归遍历,换树的左右子树
查找
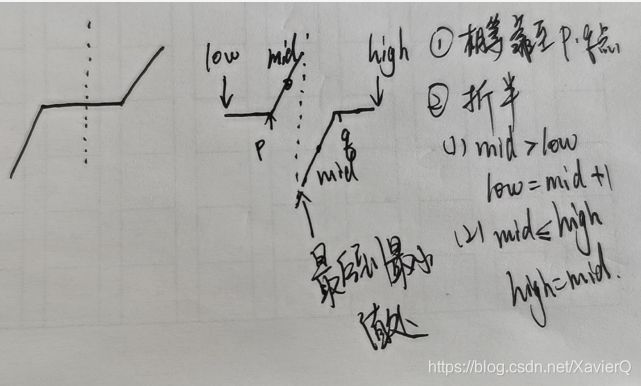
旋转数组的最小数字
一样是画图来理解
进制
二进制1的个数
用1,不断左移跟原数求与操作,只有对应位上为1才不会与出0,从而统计1的个数,同时,结束条件,一旦int型数左移超过范围,超过32,变为0
加法
先异或,再取&得进位
int carry = 0;
int res = 0;
do{
res = num1^num2;
carry = (num1 & num2) << 1;
num1 = res;
num2 = carry;
}
while(carry != 0);
return res;
代码的完整性
求数值的整数次方
别忘掉了,指数为负数的时候,结果是积分之一
数组奇前偶后
题设要求保持原顺序不变,那么用头尾双游标不能保证,那就是插入排序的原理,遍历到奇数,那么从奇数结尾到此处全部往后迭代移动,再把奇数插入空洞中
排序
求最小的k个数
采用堆排序,建堆从叶子结点往上建,注意写调整堆的算法,每次迭代往下迭代一层,然后先和右边比,再和上端比,上端大就进行调整。调整点的值最后再插入。
栈
含最小值的栈
如果元素pop()正好将最小值pop掉,无最小值,所以维护一个最小值的栈,一旦最小值出栈,将最小值栈也出栈,而新的栈顶就是新的最小值。
判断给定压入序列是否由弹出队列
仿真实现即可,栈顶等于出栈序列值,则出栈,当全部压入栈后,栈为空,说明全部按出栈序列全部弹出,没有问题。
动态规划
连续子数组的和
关注每个点前的最大子数组和,为负数,则不加上来。保证所有子序列终点上的值代表其最大值(注意动态规划的思想)
递归
字符串的全排列
public ArrayList<String> Permutation(String str) {
ArrayList<String> result = new ArrayList<String>();
StringBuilder strb = new StringBuilder(str);
if(str.length() == 1){
result.add(strb.toString());
}
else{
for(int i = 0; i < strb.length(); i++){
// 将第一位在第一位和其他与第一位相等的数放第一位的的两种情况的集合
if(i == 0 || strb.charAt(i) != strb.charAt(0)){
// 换位置
char temp = strb.charAt(0);
strb.setCharAt(0, str.charAt(i));
strb.setCharAt(i, temp);
// 获取后面位置的全排列(递归) 直接要第一位之后的,开始递归缩小规模
ArrayList<String> nstr = Permutation(strb.substring(1));
// 进行拼接,放入结果,后面的全排列很多中,和当前这种组合
for(int j = 0; j < nstr.size(); j++) {
result.add(strb.substring(0, 1) + nstr.get(j));
}
// 递归完换回来
temp = strb.charAt(0);
strb.setCharAt(0, strb.charAt(i));
strb.setCharAt(i, temp);
}
}
}
// 用例要严格按照顺序,这里,用Collections类的sort方法
Collections.sort(result);
return result;
}
思路题
顺时针打印矩阵
理想化成四条边的打印,用左上角和右上角做为定点,不停向内缩,循环打印
但要注意2*1矩阵和1*2矩阵的判断,那样的情况能套用四边;另外注意一边结束,就占用了下一边的头,不要重复打印
整数中出现1的次数
找规律题,从每10个,每百个出发
找不出规律就每个数算,不停搞得mod10/10获取1的数目
扑克牌顺子
用TreeSet,既可以利用集合特性判断是否有5张,另外通过last()和first()可以很快取到最小值和最大值
矩阵中的路径
这种回溯法问题,往上下左右走的时候直接递归走,不要判断了再走,进入下一个递归后再进行判断是否溢出等等。递归前标记走过了,注意递归结束回来要把标记去除。