【数据结构】线性表总结——基本知识要点汇总

halo~我是bay_Tong桐小白
本文内容是桐小白个人对所学知识进行的总结和分享，知识点会不定期进行编辑更新和完善，了解最近更新内容可参看更新日志，欢迎各位大神留言、指点

【更新日志】

最近更新：

• 新增内容——计算机统考408考纲要求（2020.9.13）
• 更新内容——单链表的就地逆置算法（2020.7.12）
• 更新内容——一元多项式的存储设计（2020.7.5）
• 新增内容——单链表的就地逆置（2020.7.1）
• 内容持续更新中……

计算机统考408考纲要求

2021计算机统考408考纲对线性表部分考察要求

线性表的定义及存储方式

• 定义：n个同类型数据元素构成的有限序列。
  
  
• 特点
  同一性：数据元素同类型
  有穷性：数据元素个数有穷个
  有序性：数据元素在物理或逻辑上有一定的顺序
• 存储方式：顺序存储、链式存储

顺序表工作原理

顺序表的存储结构

• 顺序存储：逻辑上相邻，物理位置也相邻
• 实现方法：一组地址连续的存储单元依次存储线性表的元素（利用数组实现）

逻辑相邻：访问某一个单元后可知其前驱或后继

物理位置相邻：内存单元物理地址连续相邻

• 特点：可通过数组下标随机存取

顺序表的查找、插入、删除操作

• 查找：按位置查找时直接通过数组下标访问对应数据单元，时间复杂度O(1)；按元素查找时遍历顺序表，时间复杂度O(n)
• 插入：直接通过下标访问数组单元进行插入，其后元素依次后移。时间复杂度O(n)
• 删除：直接通过下标访问数组单元进行删除，其后元素依次前移。时间复杂度O(n)

详细代码见基本操作集部分

单链表工作原理

单链表的存储结构

• 链式存储：逻辑上相邻，物理位置不一定相邻
• 实现方法：每个数据元素除存储自身信息外还需存储它的直接前驱或直接后继的地址信息（链表实现）

逻辑上相邻：访问某一个单元后可知其前驱或后继

物理位置不一定相邻：每个结点为随机申请的空间，物理地址不一定相邻

• 特点：存取必须从头指针开始

单链表的查找、插入、删除操作

• 查找：遍历链表，时间复杂度 O(n)
• 插入：直接通过更改指针完成元素的插入。时间复杂度O(1)
• 删除：直接通过更改指针完成元素的删除。时间复杂度O(1)

详细代码见基本操作集部分的总结

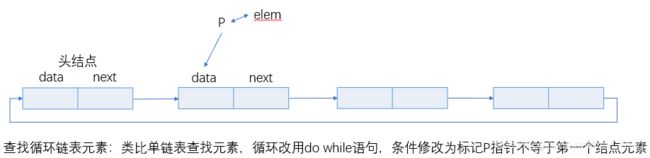
循环链表工作原理

循环单链表的存储结构

单链表的最后一个结点单元的next指针指向第一个结点单元，其它与单链表一致

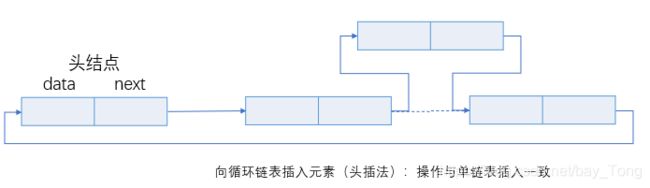
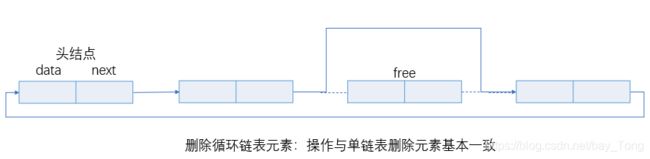
循环单链表的查找、插入、删除

详细代码见基本操作集部分

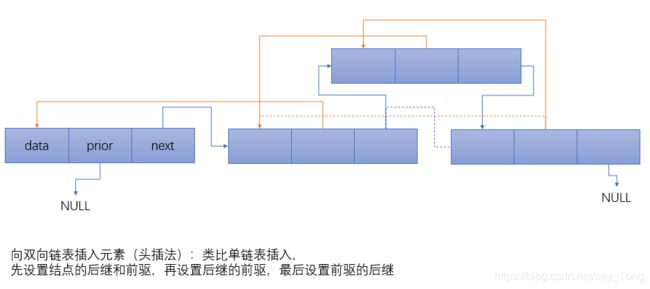
双向链表工作原理

双向链表的存储结构

既含有前驱指针又含有后继指针的链表，结合循环链表，将其首尾联系起来则可得到双向循环链表

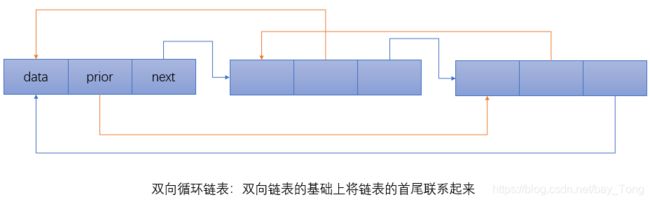
双向链表的插入、删除操作

详细代码见基本操作集部分

静态链表工作原理

• 常见场合：此方法便于在没有指针类型的高级程序语言中使用链表结构
• 存储结构：预先分配一个较大的数组空间，数组的一个分量表示一个结点，同时用游标指示器代替指针指示结点在数组中的相对位置。即通过游标作为数组下标访问数组单元，模拟链表的后继指针进行工作（工作原理与树的孩子表示法有些类似，树结构的孩子表示法详见本栏文章《树和二叉树总结——基本知识要点汇总》树的存储结构部分）。
  
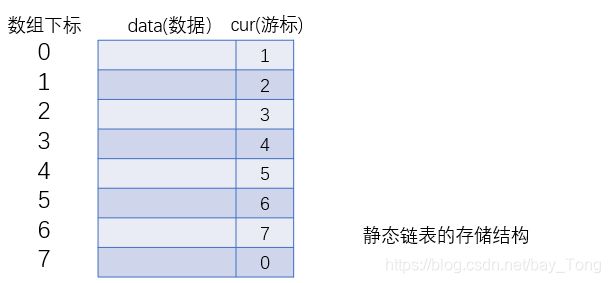
• 优点：这种结构将线性链表用一维数组进行描述，在做线性表的插入和删除操作时不需要移动元素，仅需要修改指针（即游标），仍具有链式存储结构

链表的就地逆置

• 核心思想：每次断开链表的第一个结点用头插法插入至新的链表当中（类似模拟栈的工作过程，栈的工作原理详细见本栏文章《栈和队列总结——基本知识要点汇总》）
• 实现过程

1.断开头结点，将其作为新链表的头结点，记录原链表第一个结点p及其后继q

2.断开原链表的第一个结点，头插法接在新链表之上

3.移动指针p

如此重复上述三个步骤，即可完成单链表的就地逆置。此算法在不申请额外空间的情况下完成了单链表的就地逆置，空间复杂度为O(1)

具体代码实现如下：

void Reverse_Linklist(LinkList L)
{
     
	LinkList p = L->next;//p指向表中第一个结点
	LinkList q = NULL;//q指针初始化
	L->next = NULL;//重置一个空表，即断开头结点，将其作为新链表的头结点
	while(p)
	{
     
		q = p->next;//记录原链表第一个结点p及其后继q
		p->next = L->next;//断开原链表的第一个结点，头插法接在新链表之上
		L->next = p;
		p = q;//p指向下一个要操作的结点
	}
}

相关专题——一元多项式的存储设计

关于专题详细内容，一元多项式计算器的设计实现详见本栏文章《线性表专题——一元多项式计算器的设计实现》

基本操作集汇总（代码总结）

【为了方便调用，采用多文件编程方式，代码已基本完成，实际使用时依据题目实际情况进行直接调用或简单修改后调用，算法的健壮性有待进一步测试，后续会持续对代码进行完善和优化】
【为了方便代码操作，单链表相关内容均采用带有头结点的方式进行实现】

顺序表，单链表，循环单链表基本操作集汇总（C语言实现）

【此三部分的操作集汇总在了一个头文件，在C++等语言中可使用类的封装避免函数错误调用，可通过函数的重载重写减少重复的代码量，而C语言封装性差要注意结构体的区分和函数的对应】

List.h文件

#pragma once
#ifndef LIST
#define LIST

/*线性表的顺序表、单链表、循环单链表基本操作集*/
typedef void* ElementType;
typedef int Position;

typedef struct ListArray* ListA;//线性表顺序存储
struct ListArray {
     
	ElementType* data;//数据元素顺序表
	int length;//顺序表实际长度
	int listsize;//顺序表空间大小
};

typedef struct LNode* List;//线性表链式存储
struct LNode {
     
	ElementType data;//数据元素
	List next;//指向下一结点指针
};

/*顺序表部分*/
ListA createListA(int maxsize);//创建顺序表
int isFullListA(ListA L);//判断顺序表是否已满
int searchListA(ListA L, ElementType elem);//顺序表查找元素
void InsertListA(ListA L, ElementType elem, Position p);//顺序表插入元素
void deleteListA(ListA L, ElementType elem, Position p);//顺序表删除元素
ListA mergeListA(ListA La, ListA Lb);//合并顺序表

/*单链表部分*/
List createList();//创建链表
List searchList(List L, ElementType elem);//查找链表元素
void InsertList(List position, ElementType elem);//插入链表元素（头插法）
void deleteList(List L, ElementType elem);//删除链表元素
List mergeList(List La, List Lb);//合并链表

/*循环链表部分*/
List createListCircular();//创建循环链表
List searchListCircular(List L, ElementType elem);//查找循环链表元素
void InsertListCircular(List position, ElementType elem);//向循环链表插入链表元素（头插法）
void deleteListCircular(List L, ElementType elem);//删除循环链表元素

#endif // !LIST

List.c文件

#include
#include
#include"List.h"
#define NOT_FOUND -1

/*顺序表部分*/
//创建顺序表
ListA createListA(int maxsize) {
     
	ListA L = (ListA)calloc(1, sizeof(struct ListArray));
	if (!L) {
      perror("error\n"); exit(1); }
	L->data = (ElementType*)calloc(maxsize, sizeof(ElementType));
	if (!L) {
      perror("error\n"); exit(1); }
	L->length = 0;
	L->listsize = maxsize;
	return L;
}
//判断顺序表是否已满
int isFullListA(ListA L) {
     
	if (L->length == L->listsize) {
      return 1; }
	else {
      return 0; }
}
//查找顺序表元素
int searchListA(ListA L, ElementType elem) {
     
	int i = 0;
	for (i = 0; i < L->length; i++) {
     
		if (L->data[i] == elem) {
     
			return i;
		}
	}
	return NOT_FOUND;
}//PS：与查找相关算法可结合后续章节进一步总结
//插入顺序表元素
void InsertListA(ListA L, ElementType elem, Position p) {
     
	int i = L->length;
	if (isFullListA(L)) {
      printf("顺序表已满\n"); return; }
	for (; i >= p; i--) {
     
		L->data[i] = L->data[i - 1];
	}
	L->data[p] = elem;
	L->length++;
}
//删除顺序表元素
void deleteListA(ListA L, ElementType elem, Position p) {
     
	int i = p;
	for (; i < L->length; i++) {
     
		L->data[i] = L->data[i + 1];
	}
	L->length--;
}
//合并两个顺序表
ListA mergeListA(ListA La, ListA Lb) {
     
	if (!La || !Lb) {
      printf("有表为空\n"); return NULL; }
	ListA Lc = createListA(La->length + Lb->length);
	int pa = 0, pb = 0, pc = 0;
	int pa_last = La->length - 1;
	int pb_last = Lb->length - 1;
	while (pa <= pa_last && pb <= pb_last) {
     
		if (La->data[pa] <= Lb->data[pb]) {
      Lc->data[pc++] = La->data[pa++]; }
		else {
      Lc->data[pc++] = La->data[pb++]; }
	}
	while(pa<=pa_last){
      Lc->data[pc++] = La->data[pa++]; }
	while(pb<=pb_last){
      Lc->data[pc++] = La->data[pb++]; }
	return Lc;
}

/*单链表部分*/
//创建链表
List createList() {
     
	List L = (List)calloc(1, sizeof(struct LNode));
	if (!L) {
      perror("error\n"); exit(1); }
	L->next = NULL;
	return  L;
}
//查找链表元素
List searchList(List L, ElementType elem) {
     
	List P = L->next;
	if (!L || !P) {
      return NULL; }
	while (P) {
     
		if (P->data == elem) {
     
			return P;
		}
		P = P->next;
	}
	return NULL;
}
//插入链表元素（头插法）
void InsertList(List position, ElementType elem) {
     
	if (!position) {
      printf("表位置为空\n"); return; }
	List node = createList();
	node->data = elem;
	node->next = position->next;
	position->next = node;
}
//删除链表元素
void deleteList(List L, ElementType elem) {
     
	List Pr = L;
	List P = L->next;
	while (Pr&&P) {
     
		if (P->data == elem) {
     
			Pr->next = P->next;
			free(P); return;
		}
	}
	printf("未找到指定数据元素\n");
}
//合并链表
List mergeList(List La, List Lb) {
     
	if (!La || !Lb) {
     
		return La ? La : Lb;
	}
	List Lc = La;
	List pa = La->next, pb = Lb->next, pc = Lc;
	while (pa&&pb) {
     
		if (pa->data <= pb->data) {
     
			pc->next = pa; pc = pa; pa = pa->next;
		}
		else {
     
			pc->next = pb; pc = pb; pb = pb->next;
		}
	}
	pc->next = pa ? pa : pb;
	free(Lb);
	return Lc;
}

/*循环单链表部分*/
//创建循环链表
List createListCircular() {
     
	List L = (List)calloc(1, sizeof(struct LNode));
	if (!L) {
      perror("error\n"); exit(1); }
	L->next = L;
	return L;
}
//查找循环链表元素
List searchListCircular(List L, ElementType elem) {
     
	List P = L->next;
	if (!L || !P) {
      return NULL; }
	do {
     
		if (P->data == elem) {
     
			return P;
		}
		P = P->next;
	} while (P&&P != L->next);
	return NULL;
}
//向循环链表插入链表元素（头插法）
void InsertListCircular(List position, ElementType elem) {
     
	if (!position) {
      printf("表位置为空\n"); return; }
	List node = createList();
	node->data = elem;
	node->next = position->next;
	position->next = node;
}
//删除循环链表元素
void deleteListCircular(List L, ElementType elem) {
     
	List Pr = L;
	List P = L->next;
	while (Pr&&P) {
     
		if (P->data == elem) {
     
			Pr->next = P->next;
			free(P); return;
		}
	}
	printf("未找到指定数据元素\n");
}

双向链表基本操作集汇总（C语言实现）

List_doubly.h文件

#pragma once
#ifndef LIST_DOUBLY
#define LIST_DOUBLY

typedef void* ElementType;
typedef struct LNodeDou* ListD;
struct LNodeDou {
     
	ElementType data;
	ListD piror, next;
};

ListD createListDou();//创建双向链表
ListD searchListDou(ListD L, ElementType elem);//查找双向链表元素
void InsertListDou(ListD position, ElementType elem);//向双向链表插入元素（头插法）
void deleteListDou(ListD L, ElementType elem);//删除双向链表链表元素

#endif // !LIST_DOUBLY

List_doubly.c文件

#include
#include
#include"List_doubly.h"

//创建双向链表
ListD createListDou() {
     
	ListD L = (ListD)calloc(1, sizeof(struct LNodeDou));
	if (!L) {
      perror("error"); exit(1); }
	L->piror = L->next = NULL;
	return L;
}
//查找双向链表元素
ListD searchListDou(ListD L, ElementType elem) {
     
	ListD P = L->next;
	if (!L || !P) {
      return NULL; }
	while (P) {
     
		if (P->data == elem) {
     
			return P;
		}
		P = P->next;
	}
	return NULL;
}
//向双向链表插入元素（头插法）
void InsertListDou(ListD position, ElementType elem) {
     
	if (!position) {
      printf("表位置为空\n"); return; }
	ListD node = createListDou();
	node->data = elem;
	node->next = position->next;
	node->piror = position;
	if(node->next){
      node->next->piror = node; }
	position->next = node;
}
//删除双向链表链表元素
void deleteListDou(ListD L, ElementType elem) {
     
	ListD Pr = L;
	ListD P = L->next;
	while (Pr&&P) {
     
		if (P->data == elem) {
     
			Pr->next = P->next;
			if(P->next){
      P->next->piror = Pr; }
			free(P); return;
		}
	}
	printf("未找到指定数据元素\n");
}

静态链表基本操作集

持续更新中……
我是桐小白，一个摸爬滚打的计算机小白