线段树基础知识
线段树的概念
在一类问题中,我们需要经常处理可以映射在一个坐标轴上的一些固定线段,例如说映射在OX轴上的线段。由于线段是可以互相覆盖的,有时需要动态地取线段的并,例如取得并区间的总长度,或者并区间的个数等等。一个线段是对应于一个区间的,因此线段树也可以叫做区间树。
线段树的构造思想
- 线段树是一棵二叉树,树中的每一个结点表示了一个区间[a,b]。
- 每一个叶子节点表示了一个单位区间。
- 根节点表示的是“整体”的区间。
- 对于每一个非叶结点所表示的区间[a,b]:
- 左儿子表示的区间为[a,(a+b)/2]
- 右儿子表示的区间为[(a+b)/2+1,b]
线段树示例
表示成单位线段更清楚啦~~~
线段树的运用
线段树的每个节点上往往都增加了一些其他的域。在这些域中保存了某种动态维护的信息,视不同情况而定。这些域使得线段树具有极大的灵活性,可以适应不同的需求。
例题
影子的宽度
题目描述
桌子上零散地放着若干个盒子,盒子都平行于墙。桌子的后方是一堵墙。如图所示。现在从桌子的前方射来一束平行光,把盒子的影子投射到了墙上。问影子的总宽度是多少? 
输入
第1行:3个整数L,R,N。-100000 <=L<=R<= 100000,表示墙所在的区间;1<=N<=100000,表示盒子的个数
接下来N行,每行2个整数BL, BR,-100000 <=BL<=BR<= 100000,表示一个盒子的左、右端点(左闭右开)
输出
第1行:1个整数W,表示影子的总宽度。
样例输入
Sample Input 1
0 7 2
1 2
4 5
Sample Input 2
-10 10 2
-5 2
-2 2
Sample Input 3
-10 10 3
-7 0
-4 9
-4 2
Sample Input 4
-100 100 3
-7 2
5 9
2 5
Sample Input 5
-50 50 4
-2 4
0 6
9 10
-5 30
样例输出
Sample Output 1
2
Sample Output 2
7
Sample Output 3
16
Sample Output 4
16
Sample Output 5
35
分析
这道题目是一个经典的模型。在这里,我们略去某些处理的步骤,直接分析重点问题,可以把题目抽象地描述如下:x轴上有若干条线段,求线段覆盖的总长度。 
算法1:直接模拟
设线段坐标范围为[min,max]。使用一个下标范围为[min,max-1]的一维数组,其中数组的第i个元素表示[i,i+1)的区间。数组元素初始化全部为0。对于每一条区间为[a,b]的线段,将[a,b)内所有对应的数组元素均设为1。最后统计数组中1的个数即可。 
缺点
- 此方法的时间复杂度决定于下标范围的平方。
- 当下标范围很大时,此方法效率太低。
算法2:离散化
基本思想:先把所有端点坐标从小到大排序,将坐标值与其序号一一对应。这样便可以将原先的坐标值转化为序号后,对其应用前一种算法,再将最后结果转化回来得解。
该方法对于线段数相对较少的情况有效。
[10000,22000] [30300,55000] [44000,60000] [55000,60000]
排序得10000,22000,30300,44000,55000,60000
对应得1,2,3,4,5,6
[1,2] [3,5] [4,6] [5,6] 
缺点
- 此方法的时间复杂度决定于线段数的平方。
- 对于线段数较多的情况此方法效率太低。
算法3:线段树
给线段树每个节点增加一个域cover。cover=1表示该结点所对应的区间被完全覆盖,cover=0表示该结点所对应的区间未被完全覆盖。 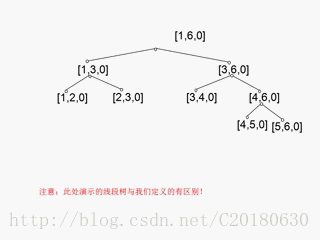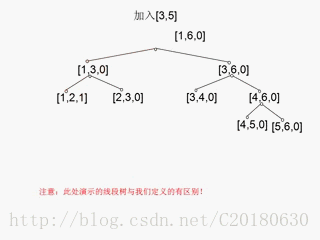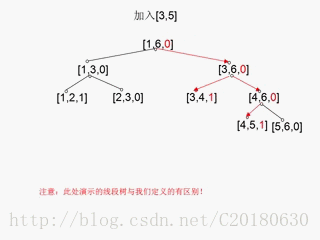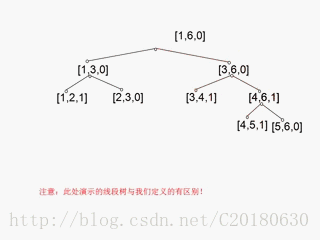
线段树的数据结构表示
1、动态数据结构
2、完全二叉树
动态数据结构
struct node {
int l, r; //区间左右端点
int tag; //区间的标记信息,可以有多种含义的标记
node *lch, *rch; //左右子区间指针
};
node *root; //线段树的根指针完全二叉树

用一个结构体数组来存储线段树,结点之间满足完全二叉树关系,即:
tree[i]的父结点是tree[i/2],
左右儿子分别是tree[i*2]和tree[i*2+1].
struct node {
int l, r; //区间左右端点
int tag; //区间的标记信息,可以有多种含义的标记
};
tree[MAXN*4]; //线段树,根为tree[1] 对于有N个单位区间的线段树,采用完全二叉树方式来存储,需要开多大的数组呢?
可以证明,区间长度为N的线段树的总节点数等于2N-1。因此基本上开2N的空间就足够了。但在下面这种实现中,需要开4N的空间才行!
基本函数
void build(int i, int l, int r)//建树
{
int mid;
tree[i].l = l; tree[i].r = r;
tree[i].cover = 0;
if (r == l ) return; //是单位区间,则返回
mid = (l + r) / 2;
build(i * 2, l, mid);
build(i * 2 + 1, mid + 1, r);
}
void insert(int i, int l, int r)//插入
{
int mid;
if (tree[i].cover == 1) return; //当前区间已经覆盖,返回
mid = (tree[i].l + tree[i].r) / 2;
if (l==tree[i].l && r==tree[i].r) //恰好与当前区间重合
tree[i].cover = 1;
else if (r <= mid) //仅在左子区间
insert(i * 2, l, r);
else if (l >= mid + 1)
insert(i * 2 + 1, l, r); //仅在右子区间
else //分在左右区间
{
insert(i * 2, l, mid);
insert(i * 2 + 1, mid + 1, r);
}
}
int count(int i)//统计
{
if (tree[i].cover == 1)
return tree[i].r - tree[i].l + 1;
else
if (tree[i].l == tree[i].r ) return 0;
else return count(i*2) + count(i*2+1);
}这是一个遍历线段树的过程。
主函数
在我们采用的方法中,区间的端点不能是负数,最小要从0开始。因此对题目中有负数区间的情况,需要迁移到非负区间来做。
int main()
{
int i, j, k, XO;
scanf("%d%d%d", &l, &r, &m);
XO = -l;
l += XO; r += XO;
build(1, l, r-1);
for (i=1; i<=m; i++)
{
scanf("%d%d", &j, &k);
j += XO; k += XO;
insert(1, j , k-1);
}
ans = count(1); printf("%d\n", ans);
return 0;
}源代码
#include另一种插入算法
我们在前面的插入算法时要考虑当前结点的区间与参数中的插入区间的多种交叉情况,而且参数中传递的插入区间一直在变。更简单的做法是:保持参数中的插入区间一直不变,然后看与当前结点区间的关系,具体实现看代码:
void insert(int i,int l,int r)
{
if (rreturn; //不相交,返回
if (l<=tree[i].l && tree[i].r<=r) //全盖,返回
{
tree[i].cover = 1;
return;
}
insert(i*2,l,r);
insert(i*2+1,l,r);
} 区间标记的改进
在前面的线段树中,我们定义的区间标记cover表示当前区间是否被一条线段覆盖。在这种下定义下,回答一次查询的时间是O(N)的。
如果题目改成M个查询,每个查询是问一个子区间的覆盖情况,显然总的时间将为O(M*N)。如果M很大,显然会超时。能不能把回答一次查询的时间改成O(logN)?
定义标记sum表示区间内被线段覆盖的总长度。当查询到这个区间时,就可以直接返回sum的值,而不必向下递归查询。这样就把时间减小到O(logN)。
当然要使整个运行时间减小,还要保证insert操作的时间不变。也就是说,要能在insert操作时及时更新sum的值,使之正确反映区间线段的覆盖情况。
实现
void insert(int i,int l,int r)
{
if (rreturn; //不相交,返回
if (l<=tree[i].l && tree[i].r<=r) //全盖,直接得解,返回
{
tree[i].sum=tree[i].r-tree[i].l+1; //更新sum
return;
}
if (tree[i].sum == tree[i].r-tree[i].l+1) return; //区间已经盖满
if (tree[i*2].sum2].r-tree[i*2].l+1) insert(i*2,l,r);
if (tree[i*2+1].sum2+1].r-tree[i*2+1].l+1) insert(i*2+1,l,r);
tree[i].sum = tree[i*2].sum+tree[i*2+1].sum; //更新sum
} 回答查询
当把区间标记改为sum,对于例1而言,只需要直接输出tree[1].sum就可得解。我们省掉了count函数去统计区间的覆盖情况。
源代码
#includereturn;
if(l<=tree[i].l&&tree[i].r<=r){
tree[i].sum=tree[i].r-tree[i].l+1;
return;
}
if(tree[i].sum==tree[i].r-tree[i].l+1) return;
if(tree[i*2].sum2].r-tree[i*2].l+1) insert(i*2,l,r);
if(tree[i*2+1].sum2+1].r-tree[i*2+1].l+1) insert(i*2+1,l,r);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
}
int main()
{
int XO;
scanf("%d%d%d",&l,&r,&m);
XO=-l;l+=XO;r+=XO;
build(1,l,r-1);
for(int i=1;i<=m;i++){
int bl,br;
scanf("%d%d",&bl,&br);
bl+=XO;br+=XO;
insert(1,bl,br-1);
}
printf("%d",tree[1].sum);
} 盒子的个数
题目描述
桌子上零散地放着若干个盒子,盒子都平行于墙。桌子的后方是一堵墙。如图所示。问从桌子前方可以看到多少个盒子?假设人站得足够远。 
输入
第1行:3个整数L,R,N。-100000 <=L<=R<= 100000,表示墙所在的区间;1<=N<=100000,表示盒子的个数
接下来N行,每行2个整数BL, BR,-100000 <=BL<=BR<= 100000,表示一个盒子的左、右端点(左闭右开)。越在前面输入的盒子越排在离墙近的位置,后输入的盒子排在离墙远的位置。
输出
第1行:1个整数M,表示可看到的盒子个数。
样例输入
1 10 5
2 6
3 6
4 6
1 2
3 6
样例输出
3
分析
可以这样来看这道题:x轴上有若干条不同线段,将它们依次染上不同的颜色,问最后能看到多少种不同的颜色?(后染的颜色会覆盖原先的颜色)
我们可以这样规定:x轴初始无颜色,第一条线段染颜色1,第二条线段染颜色2,以此类推。
原先定义的线段树标记不再适用,但是我们可以通过修改线段树的标记的定义,使得这道题也能用线段树来解。
定义标记color如下:color=-1表示该区间由多种颜色组成。color>=0表示该区间只有一种单一的颜色覆盖。
插入算法
- 在当前区间覆盖一条左右端点为l,r,颜色为color的线段,有哪些情况呢?
- 当前区间与线段不相交
- 当前区间被线段完全覆盖
- 当前区间与线段部分相交
对于部分相交的情况,要进一步判断当前区间是否是纯色,如果是则需要把当前区间的颜色传递到左右子区间,并把当前区间改成杂色。
void insert(int k,int l,int r,int color)
{
if (rreturn;
if (l<=tree[k].l && tree[k].r<=r)
{
tree[k].color=color;
return;
}
if (tree[i].color>=0)
{
tree[i*2].color=tree[i*2+1].color=tree[i].color;
tree[i].color=-1;
}
insert(i*2,l,r,color);
insert(i*2+1,l,r,color);
} 统计算法
使用一个数组Flag,初始化为0。遍历线段树,对于每种颜色c对Flag[c]赋值1。最后统计Flag中1的个数即可。
void find(int i)
{
if (tree[i].color==0)return;
if (tree[i].color>0)
{
col[tree[i].color]=1;
return;
}
if (tree[i].color==-1)
{
find(i*2);
find(i*2+1);
}
}源代码
#includereturn;
if(l<=tree[k].l&&tree[k].r<=r){
tree[k].color=color;
return;
}
if(tree[k].color>=0){
tree[k*2].color=tree[k*2+1].color=tree[k].color;
tree[k].color=-1;
}
insert(k*2,l,r,color);
insert(k*2+1,l,r,color);
}
void find(int k){
if(tree[k].color==0) return;
if(tree[k].color>0){
col[tree[k].color]=1;
return;
}
if(tree[k].color==-1){
find(k*2);
find(k*2+1);
}
}
int main()
{
scanf("%d%d%d",&l,&r,&n);
int XO=-l;
l+=XO;r+=XO;
build(1,l,r-1);
int bl,br;
for(int i=1;i<=n;i++){
scanf("%d%d",&bl,&br);
bl+=XO;br+=XO;
insert(1,bl,br-1,i);
}
find(1);
int ans=0;
for(int i=1;i<=n;i++)
ans+=col[i];
printf("%d",ans);
} 
