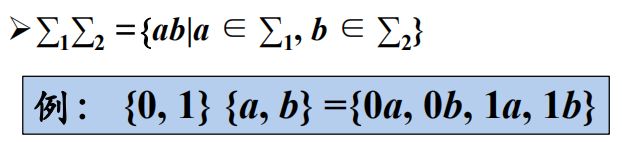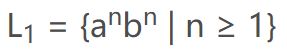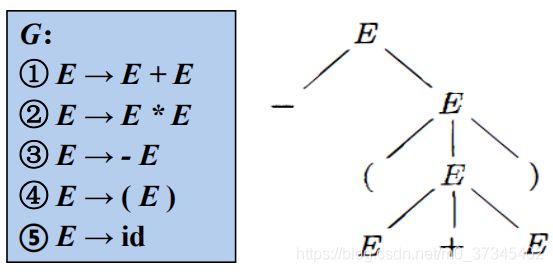编译原理-2-程序设计语言及其文法

目录

 1 基本概念

（1）字母表

（2）串(String)

2 文法的定义

3 语言的定义

  (1)推导(Derivations)和规约(Reductions)

（2）句型和句子

（3）语言的形式化定义

4 文法的分类

（0）0型文法 (Type-0 Grammar)

（1）1型文法 (Type-1 Grammar)

（2）2型文法 (Type-2 Grammar)

（3）3型文法 (Type-3 Grammar)

（4）文法的判别

5 CFG的分析树 

（1）分析树是推导的图形化表示

（2）（句型的）短语

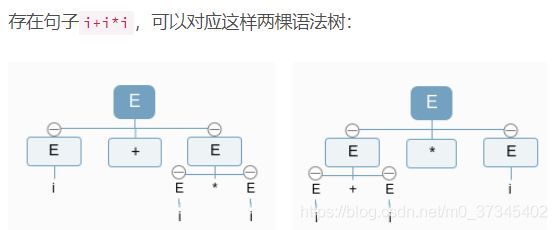
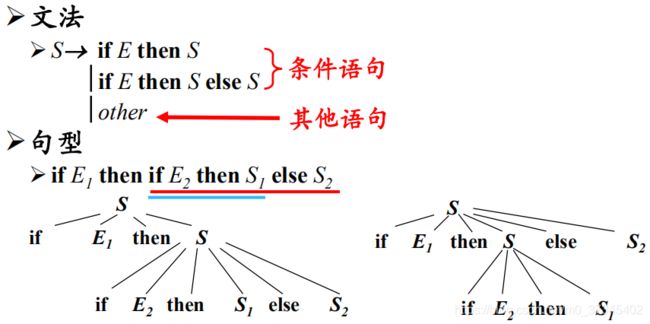
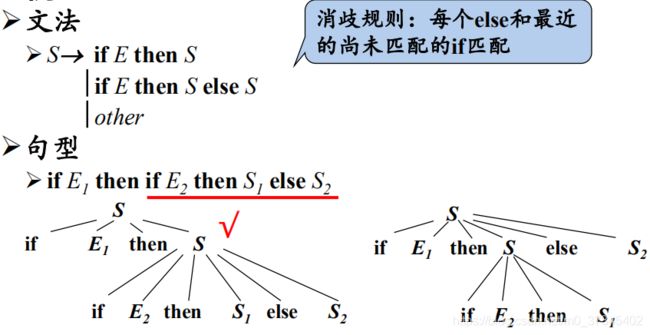
（3）二义性文法

---

 1 基本概念

（1）字母表

字母表∑ 是一个 有穷符号集合 (符号：字母、数字、标点符号)

字母表上的运算

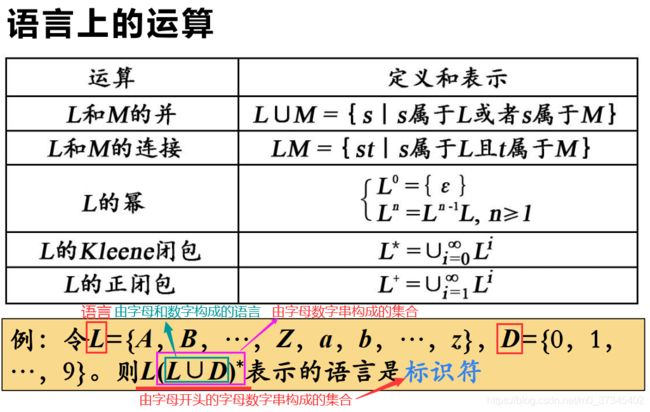
字母表∑1和∑2的乘积( product)                                            字母表∑的n次幂( power)

字母表∑的正闭包( positive closure)                                      字母表∑的克林闭包(Kleene closure)

（2）串(String)

 

➢设 ∑ 是一个字母表，  x ∈ ∑ * ， x 称为是 ∑ 上的一个 串 ； 串是字母表中 符号的 一个 有穷序列

➢串 s 的 长度 ，通常记作 | s | ，是指 s 中 符号的个数 ；例: | aab|=3

➢ 空串 是 长度为 0 的串 ，用 ε （ epsilon ） 表示 ； | ε|= 0

串上的运算

①连接                                                                                    ②幂

    

 

2 文法的定义

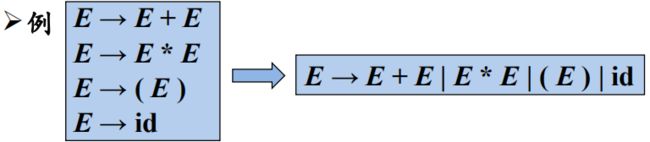
（1）文法的形式化定义

文法是由非终结符（大写字母）和终结符（小写字母）以及“—>”组成的。例：A—> a、B—>dba、S—> Ab、adB—>d

G表示文法，文法由一个四元组定义 。

① VT​：终结符集合(terminal symbol)

• 不能单独出现在推导式左边的符号，也就是说终结符不能再进行推导。
• 终结符是一个形式语言的基本符号。就是说，它们能在一个形式语法的推导规则的输入或输出字符串存在，而且它们不能被分解成更小的单位。 一个语法的规则不能改变终结符。

终结符(terminal symbol)是文法所定义的语言的基本符号，有时也称为token。 例如：VT={apple,boy,eat,little}

例如，下面的语法有两个规则：

1. x -> xa
2. x -> ax

在这种语法之中，a是一个终结符，因为没有规则可以把a变成别的符号。不过，有两个规则可以把x变成别的符号，所以x是非终结符。一个形式语法所推导的形式语言必须完全由终结符构成。

② VN​：非终结符集合(nonterminal)

• 非终结符(nonterminal) 是用来表示语法成分的符号，有时也称为“语法变量”。不是终结符的都是非终结符。非终结符可理解为一个可拆分元素，而终结符是不可拆
  分的最小元素。
• 非终结符是可以被取代的符号。一个形式文法中必须有一个起始符号；这个起始符号属于非终结符的集合。
• 在上下文无关文法中，每个推导规则的左边只能有一个非终结符而不能有两个以上的非终结符或终结符。并非所有的语言都可以被上下文无关文法产生。

③ P​：产生式集合

④ S：开始符号

S∈V N 。 开始符号 ( start symbol)表示的是该文法中最大的 语法成分   ➢例：S = <句子>

（2）产生式的简写

对一组有 相同左部 的 α 产生式 α → β 1 , α → β 2 , … , α → βn

可以简记为： α → β 1 | β 2 | … | β n    读作： α 定义为 β 1 ，或者 β 2 ， … ，或者 β n 。β 1 ， β 2 ， … ， β n 称为 α 的 候选式 ( Candidate)

 （3）符号约定

①终结符:

• 字母表中排在前面的小写字母，如 a、b、c
• 运算符，如 +、*等
• 标点符号，如括号[ ]( )、逗号等
• 数字0、1、. . . 、9
• 粗体字符串，如id、if等

②非终结符:

• 字母表中排在前面的大写字母，如A、B、 C
• 字母S。通常表示开始符号
• 小写、斜体的名字，如 expr、stmt等
• 代表程序构造的大写字母。如E(表达式)、T(项) 和F(因子)

③

• 字母表中排在后面的大写字母（如X、Y、Z） 表示文法符号（即终结符或非终结符）
• 字母表中排在后面的小写字母（主要是u、v、. . . 、z） 表示终结符号串（包括空串）
• 小写希腊字母，如α、β、γ，表示文法符号串（包括空串）
• 除非特别说明，第一个产生式的左部就是开始符号

3 语言的定义

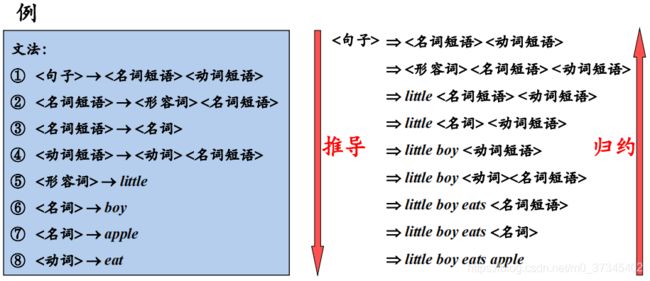
(1)推导(Derivations)和规约(Reductions)

• 给定文法G=(VT , VN , P , S )，如果 α→β ∈ P，那么可以将符号串γαδ中的α替换为β，也就是说，将γαδ 重写(rewrite)为γβδ，记作 γαδ ⇒ γβδ。此时，称文法中的符号串 γαδ 直接推导(directly derive)出 γβδ
• 即用产生式的右部替换产生式的左部

（2）句型和句子

如果 S⇒ * α ， α ∈ ( V T ∪ V N ) * ，则称 α 是 G 的一个 句型 ( sentential form)

• 一个句型中既可以包含终结符，又可以包含非终结符，也可能是空串

如果 S⇒ * w ， w ∈ V T * ，则称 w 是 G 的一个 句子 ( sentence)

• 句子是不包含非终结符的句型
• 推导就是将上下文无关文法转化为句子的过程

（3）语言的形式化定义

由文法G 的开始符号 S 推导出的所有句子构成 的集合称为 文法G生成的语言 （language） ，记为 L (G )。 即L( G ) = {w | S⇒ * w,w ∈ V T * }

4 文法的分类

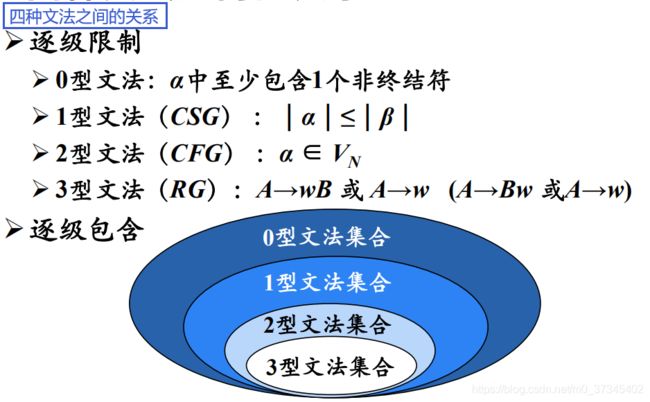
Chomsky文法分类将文法分为四种，逐渐对产生式施加限制形成一个层次：

每种正则文法都是上下文无关的，每一种上下文无关文法都是上下文有关的，而每一种上下文有关文法都是0型文法

（0）0型文法 (Type-0 Grammar)

• 无限制文法(Unrestricted Grammar) / 短语结构文法 (Phrase Structure Grammar, PSG )
• 规则形式：α → β，α,β∈(VT,VN) *，α ≠ ε
• 0型语言   由0 型文法 G 生成的语言 L ( G )

（1）1型文法 (Type-1 Grammar)

• 上下文有关文法(Context-Sensitive Grammar , CSG )
• 规则形式 ∀α → β∈P，｜α｜≤｜β｜    产生式的一般形式： α1Aα2 → α1βα2 ( β≠ε )

• 1型文法在0型文法的基础上进一步要求产生式的左部α中符号的个数不能多于β中符号的个数
• 非终结符A，当它的上下文分别是α1和α2的时候才可以替换为β，因此是上下文有关的
• 上下文有关文法中不包含空产生式，空产生式就是产生式的右部β是空串的产生式

        如果上下文有关文法中包含空产生式，那么β的长度就为0，而我们要求α中至少包含一个非终结符，所以α 的长度至少          为1，那么α的长度大于等于1，而β的长度等于0这就与上下文有关文法的定义不符合，所以上下文有关文法中就不包含        空产生式

• 上下文有关语言（1型语言） 由上下文有关文法 (1型文法) G生成的语言L(G )

（2）2型文法 (Type-2 Grammar)

• 上下文无关文法 (Context-Free Grammar, CFG )
• 规则形式 ∀α → β∈P，α ∈ VN  产生式的一般形式：A→β

• 2型文法就是上下文无关文法，左部α必须是一个非终结符，大写字母A定义的是非终结符，
• 将A转换为β不需要考虑上下文，所以称为上下文无关文法
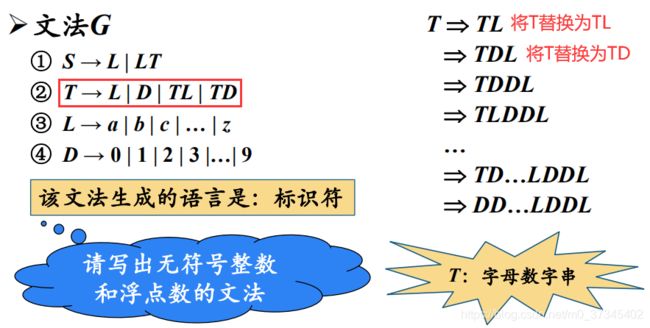
• 下面用来生成标识符的文法的左部被称为非终结符，称为上下文无关文法

• 上下文无关语言（2型语言）

（3）3型文法 (Type-3 Grammar)

• 正则文法 (Regular Grammar, RG )

        · 右线性(Right Linear)文法： A→wB 或 A→w

        · 左线性(Left Linear) 文法： A→Bw 或 A→w

        · 左线性文法和右线性文法都称为正则文法

 

• 右线性文法在2型文法的基础上继续对产生式的右部进行限制，也就是说右线性文法的右部要么是终结符号串w，要么就是在终结符右边添加一个非终结符B；左线性文法的话要么是一个终结符，要么是在终结符左边加一个非终结符
• 在正则文法的表达式的右部最多只有一个非终结符
• 不仅标识符可以用正则文法来描述，程序设计语言中的大多数单词都可以用正则文法来描述

• 正则语言（3型语言）

（4）文法的判别

从最复杂的3型进行判断，如果不符合3型的，那再看是不是2型的，依次向下判断，最后答案取其最高的符合规则。

给出下面语言的相应文法，并指明其类型
① 

解：S → a…ab…b 两边分别加上a和b得到：S → a(a…ab…b)b 即S → aSb ；
      又因为 n ≥ 1,得出S → ab，所以，文法为S → aSb|ab，为2型上下文无关文法。

②

解：S → a…ab…bc…c , 记A → a…ab…b , B→ c…c；S → AB
由A → a(a…ab…b)b 得 A → aAb
又因为 n ≥ 1,得出A → ab，A → aAb | ab
由B → c(c…c)可得B→ cB，又因为 i ≥ 0,得出B → ε，B→ cB | ε
所以，文法为：
S → AB
A → aAb | ab
B→ cB | ε
2型上下文无关文法

③

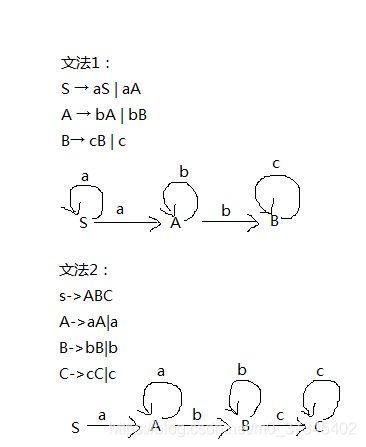
S → a…ab…bc…c ,得S → a(a…ab…bc…c)，S → aS
由i ≥ 1可得 S → a(b…bc…c)，记A→ b…bc…c 得 S → aA；又因为 A→ b(b…bc…c),得出A → bA
又因为 j ≥ 1,得出 A→ b(c…c)，记B → c…c 得 A → bB；由B → c(c…c)可得B→ cB
有因为k ≥ 1,可得B→ c
所以，文法为：
S → aS | aA
A → bA | bB
B→ cB | c
3型右线性文法

5 CFG的分析树 

• 根节点的标号为文法开始符号
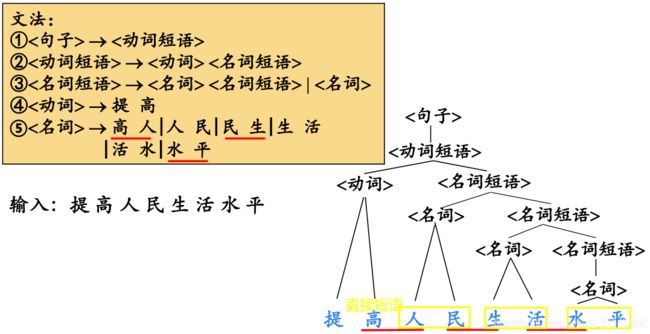
• 内部结点表示对一个产生式A→β的应用，该结点的标号是此产生式左部A 。该结点的子结点的标号从左到右构成了产生式的右部β
• 叶结点的标号既可以是非终结符，也可以是终结符。从左到右排列叶 节点得到的符号串称为是这棵树的产出( yield )或边缘(f rontier)

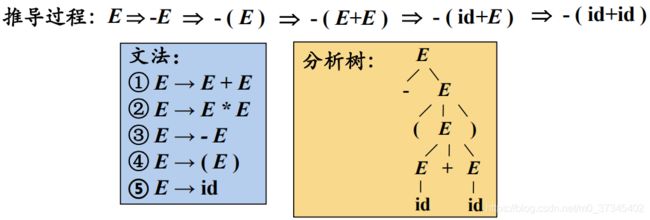
（1）分析树是推导的图形化表示

给定一个推导 S ⇒ α 1⇒ α 2⇒ …⇒ α n ，对于推导 过程中得到的每一个 句型 α i ，都可以构造出一个 边缘为 α i 的 分析树

（2）（句型的）短语

--短语

句型的分析树中的每一棵子树的边缘称为该句型的一个短语(phrase) ；一个句型的语法树中任一子树叶结点所组成的符号串都是该句型的短语。

--直接短语

如果子树只有父子两代结点，那么这棵子树的边缘称为该句型的一个直接短语(immediate phrase)；

所有子树中，深度为2的子树的叶子节点串就是直接短语；

如果子树中不再包含其他的子树，即A只能推导出b，而b不能再推出其他的式子，则b为此句型的直接短语。

--句柄

直接短语中的最左直接短语为该句型的句柄。

--素短语 

指一个短语至少包含一个终结符，并且除它自身之外不再包含其他素短语；

从短语集合中找出所有含有终结符的短语，然后选出除它自身之外不再含更小的素短语（这个小的概念是集合中没有被包含的元素，如有两个短语aAA和aAAA，aAA含于aAAA，所以aAA比aAAA小）

--最左素短语

从素短语集合中找出最左边的素短语。

​​

判别直接短语例子：

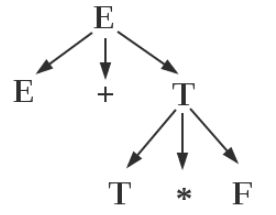如果能画出对应的抽象语法树，则就表明此表达式是文法的一个句型.

按如上的语法树可知，E=T*F为此文法的一个句型:

• 短语: T*F, E+T*F

• 直接短语：T*F

• 句柄：T*F

2.

S -> a|b|(T) 
T -> TdS|S
证明(Sd(T)db)是S的一个句型，并求出短语，直接短语，句柄

由 抽象语法树 可得S=(Sd(T)db)为此文法的一个句型：

• 短语:S，(T)，b，Sd(T)，Sd(T)db，（Sd(T)db)

• 直接短语:S，(T)，b

• 句柄:S

（3）二义性文法

如果一个文法可以为某个句子生成 多棵分析树 ， 则称这个文法是 二义性 的

如果一个文法中存在某个句子(全部由终结符组成的句型)对应两棵不同的语法树，则该文法具有二义性，如文法：

G(E):
    E->i
    E->E+E
    E->E*E

语言的二义性

如果一个语言可以由不同文法来描述，那么这个语言是具有二义性的。特别地，如果所有能产生该语言的二型文法都是二义性文法，那么称这个语言是 先天二义的

二义性文法的判定

对于任意一个上下文无关文法，不存在一个算法， 判定它是无二义性的；但能给出一组 充分条件 ，满足这组充分条件的文法是无二义性的。

➢满足，肯定无二义性

➢不满足，也未必就是有二义性的