使用Numpy拟合贝塞尔曲线

贝塞尔曲线: 通过起点、终点以及多个控制点绘制得到的曲线，Photoshop中的钢笔工具就是贝塞尔曲线。另外，CSS中动画的计时函数也有三次贝塞尔曲线，例如常用的ease - cubic-bezier(0.25,0.1,0.25,1), ease-in-out - cubic-bezier(0.42,0,0.58,1)。贝塞尔曲线的通用计算公式为$B(t)={\Sigma }_{i=0}^n\left(\genfrac{}{}{0ex}{}{n}{i}\right)Pi(1-t{)}^{n-i}{t}^i,0\le t\ge 1$，其中t可以理解为时刻，Pi表示控制点(包括起终点)。

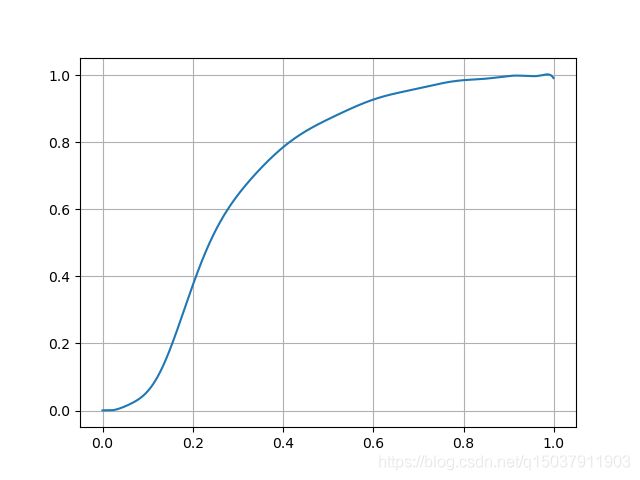
本文使用Numpy拟合三次贝塞尔曲线cubic-bezier(0.3,0,0,1)，其图像如下:

拟合后的结果如下:

可以使用geogebra查看拟合后的曲线在整个坐标轴上的结果，本文中拟合后的结果为:$-5634657.187995095x^{16}+45207123.80406813x^{15}+-164321160.9410473x^{14}+357735878.3266866x^{13}+-519499735.0536763x^{12}+530305734.45764804x^{11}+-390543484.20302945x^{10}+209498881.24963355x^9+-81592649.14667341x^8+22708417.585277304x^7+-4379479.970961253x^6+556579.9351615013x^5+-43295.904223406396x^4+1880.8424521764407x^3+-32.99834229194805x^2+0.19434715012662382x^1+0.0003451401468581472x$，挺长的emmm

拟合过程:

1. 以间隔0.001计算每个t时对应的坐标(x,y)
2. 使用pyplot绘制曲线
3. 使用np.polyfit(x, y, deg)拟合曲线
4. 绘制拟合后的曲线，根据结果调整deg参数(即多项式的最高次)

代码如下

from matplotlib import pyplot as plt
import numpy as np

p0 = (0, 0)
p1 = (0, 0)
p2 = (1, 1)
p3 = (1, 1)

def calculateP(t: float):
    """ 
    根据p0~p3计算时刻t曲线的坐标，0 <= t <= 1，曲线: cubic-bezier(.4,0,0,1)  
    p0      p1          p2      p3  
    (0, 0)  (0.4, 0)    (0, 1)  (1, 1)

    返回一个(x, y)
    """
    tmp = 1 - t
    x = p0[0] * pow(tmp, 3) + 3 * p1[0] * t * pow(tmp, 2) + 3 * \
        p2[0] * pow(t, 2) * tmp + 1 * p3[0] * pow(t, 3)
    y = p0[1] * pow(tmp, 3) + 3 * p1[1] * t * pow(tmp, 2) + 3 * \
        p2[1] * pow(t, 2) * tmp + 1 * p3[1] * pow(t, 3)
    return (x, y)

def getPoints(dis, calc: callable):
    """ 
    获取三次贝塞尔曲线的离散点，参数 dis 指定离散点的间距，calc 指定计算函数

    返回一个坐标列表[(x,y)] 
    """
    if dis <= 0:
        return [(0, 0)]
    t = 0
    res = []
    while t < 1:
        res.append(calc(t))
        t += dis
    return res

def showCurve(points):
    """ 绘制 points 中的点 """
    # plt.figure(figsize=(5, 5))
    plt.subplot()
    plt.grid()
    plt.plot([p[0] for p in points], [p[1] for p in points])
    plt.show()

def work():
    global p1
    global p2
    dis = 0.001
    p1 = (0.3, 0)
    p2 = (0, 1)
    points = getPoints(dis, calculateP)
    showCurve(points)
    f = np.polyfit([p[0] for p in points], [p[1] for p in points], 16)
    print([x for x in f])
    f = np.poly1d(f)
    npoints = getPoints(dis, lambda x: (x, f(x)))
    showCurve(npoints)