0-1背包&算法练习10& 部分题

问题 A: ly的小迷弟

题目描述
众所周知ly虽然是个小胖子，但是长得还是很好看的，所以她有很多小迷弟(bu cun zai de)，但是ly当然不是个只看颜值的人了，所以在她觉得颜值还可以的所有人里，把这些人选出来按照智商排序…
虽然wjw不是ly的小迷弟，但是wjw很想知道某个智商值在这群人里能排多少名，那么只能麻烦你帮他了

输入
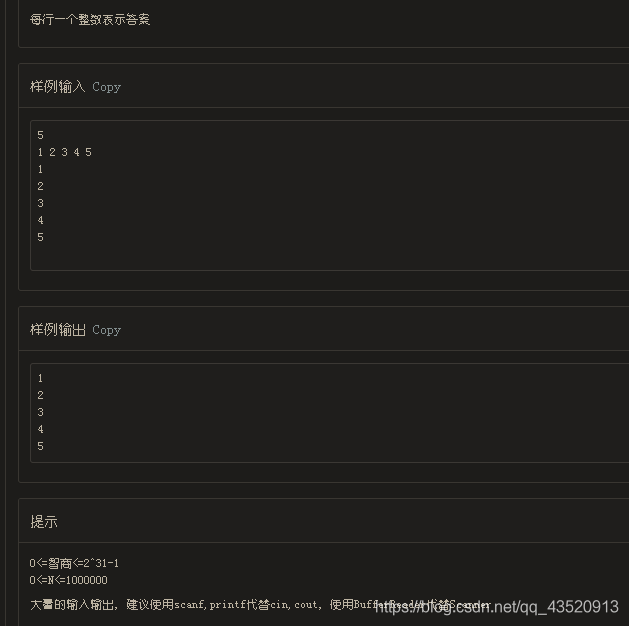
第一行一个整数N表示有N个被选出来的小迷弟
第二行N个整数分别表示这N个小迷弟的智商
接下来若干行表示wjw的询问，每行一个智商值

输出
每行一个整数表示答案

#include

#define ll long long

using namespace std;
const int N=1000005;
int a[N];
int main()//这题有点卡时间，用sort排序后，二分查找就能过
{
     
    int T;
    int n;
    scanf("%d",&T);
    a[0]=0;
  for(int i=1;i<=T;i++){
     
    scanf("%d",&a[i]);
  }

  sort(a,a+T+1);
  while(~scanf("%d",&n)){
     //二分查找
     int low=0,hight=T;
        while(low<=hight){
     
            int mid=(low+hight)/2;
            if(n>a[mid]){
     
               low=mid+1;
            }else if(n<a[mid]){
     
                hight=mid-1;
            }else if(n==a[mid]){
     
                 printf("%d\n",mid);
                 break;
            }
        }





  }
    return 0;
}

问题 B: ly的仓鼠

题目描述
上完体育课的ly很无聊，于是准备去蹭一蹭临床专业的课程,正好今天他们准备研究一些仓鼠的基因，由于操作有点出错…ly得到了一段很长很长的基因链（都是由小写字母构成），作为一个好奇心极强的人，ly有了一个问题，每次取两个区间，用这两个区间的DNA生产出来的仓鼠，会是两只一模一样的仓鼠吗？
显然小胖子ly光有好奇心并没有那个能力去得出结果…只会提问不会解答,所以又要麻烦你帮她了。
输入
第一行输入两个正整数n,q，分别代表DNA串的长度以及要询问的次数。
第二行一个字符串S，表示ly得到的DNA序列
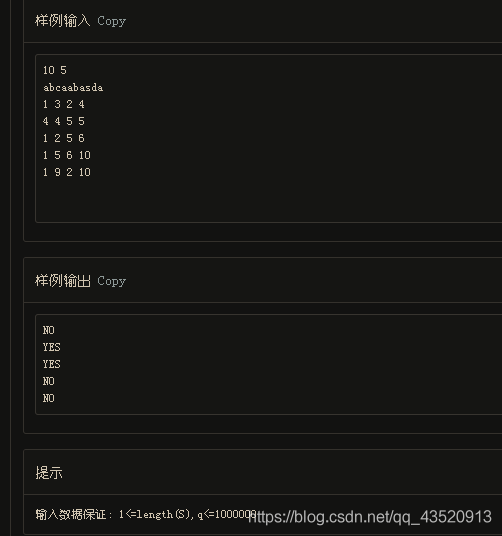
下面q行每行输入四个整数l1,r1,l2,r2分别代表q次询问，对于每一次询问请你判断两个[l,r]区间的DNA是否相同。
输出
对于每一个询问 相同输出YES不相同输出NO
数据量较大，建议使用scanf,printf输入输出

#include
using namespace std;
string s;
int T,n,l1,r1,l2,r2; 
int main(){
     //这道题的关键是注意输入数据的合法性，对数据进行判断
    while(~scanf("%d%d",&T,&n)){
     
        cin>>s;
        for(int i=0;i<n;i++){
     
            scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
            if(r1>T||r2>T){
     //数据处理1，排查
                printf("NO\n");
            }
            else if((r1-l1)!=(r2-l2))printf("NO\n");//数据处理2，长度不一致，排除
            else {
     
                string s1=s.substr(l1-1,r1-l1+1);
                string s2=s.substr(l2-1,r2-l2+1);
                if(s1==s2)printf("YES\n");
                else printf("NO\n");
            }
        }
    }
    return 0;
}

问题 C: wjw的星期五

题目描述
wjw最近运气极其差，什么roll点1-100连着十次都是个位数啊，买个珍珠奶茶没有珍珠啊，吃方便面没有调料包啊…
迷信的wjw觉得，一定是因为这个月的13号正好是星期五，才会导致他的运气这么差。
现在他想知道，在某个年份中，有多少个月的13号是星期五，这样他才可以提前做好心理准备。
PS.已知1998年1月1日是星期四，输入的年份肯定大于或等于1998年。

输入
input
输入只有一行，表示年份(大于等于1998年)

输出
output
输出只有一行，表示这一年中有多少个月的13号是星期五

对于公式加年份2月的处理

#include

#define ll long long

using namespace std;


int main()
{
     
    int year,sum;
    int day[13]={
     0,31,28,31,30,31,30,31,31,30,31,30,31};
    while(scanf("%d",&year)!=EOF)
    {
     
      int days=0;
      for(int i=1998;i<year;i++)
      {
     
          if(i%4==0&&i%100!=0||i%100==0&&i%400==0)
            days+=366;
          else
            days+=365;                             
      }
      sum=0;
      if(year%4==0&&year%100!=0||year%100==0&&year%400==0)  
      {
     
         day[2]=29;
         for(int i=1;i<=12;i++)       
         {
     
            if((days+13)%7==2)    
                sum++;
            days+=day[i];
         }
      }
      else                           
      {
     
        day[2]=28;
        for(int i=1;i<=12;i++)
        {
     
           if((days+13)%7==2)
             sum++;
            days+=day[i];
        }
      }
      printf("%d\n",sum);
    }
   return 0;
}

问题 D: 0-1背包问题

题目描述
给定n种物品和一个背包，物品i的重量是Wi，其价值为Vi，背包的容量为C。如何选择装入背包的物品，可以使得装入背包中物品的总价值最大？
输入
每组输入包括三行，
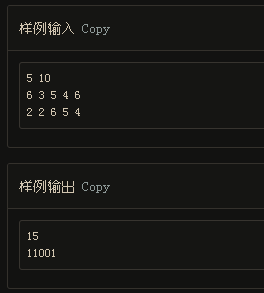
第一行包括物品个数n，以及背包容量C。
第二、三行包括两个一维数组，分别为每一种物品的价值和重量。
输出
输出包括两行，第一行为背包的最大总价值，第二行为所选取的物品。
例如：最大总价值=15，物品选取策略为11001。

#include

#define ll long long
const int N=1005;
using namespace std;

int a[N][N];
int w[N];
int num[N];
int code[N];
int main()
{
     
    int T,n;
    while(cin>>T>>n){
     
           for(int i=1;i<=T;i++){
     
            scanf("%d",&num[i]);
           }
            for(int j=1;j<=T;j++){
     
            scanf("%d",&w[j]);
           }
           for(int k=1;k<=T;k++){
     
                for(int m=0;m<=n;m++){
     
                    if(k==1){
     
                        if(w[k]>m){
     
                            a[k][m]=0;
                        }else{
     
                            a[k][m]=num[k];
                        }
                        continue;
                    }
                    if(w[k]>m){
     
                            a[k][m]=a[k-1][m];
                        }else{
     
                            a[k][m]=max(a[k-1][m-w[k]]+num[k],a[k-1][m]);
                        }
                }
           }
          int temp=n;
           for(int x=T;x>0;x--){
     
                if(a[x][temp]==a[x-1][temp]){
     
                    code[x]=0;
                }else{
     
                    code[x]=1;
                    temp=temp-w[x];
                }
           }
           printf("%d\n",a[T][n]);
           for(int ii=1;ii<=T;ii++){
     
                printf("%d",code[ii]);
           }
           printf("\n");
    }
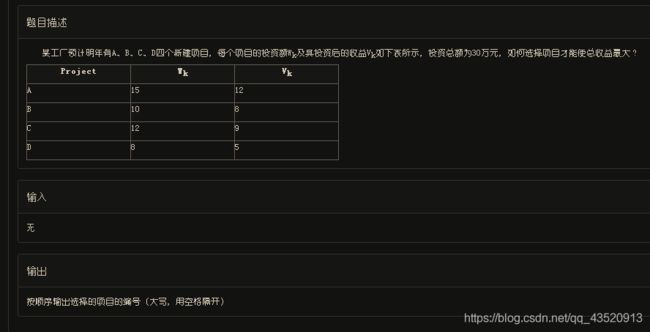
   return 0;
}

问题 E: 投资

#include

#define ll long long
const int N=1005;
using namespace std;

int a[N][N];
int w[N];
int num[N];
int code[N];
int main()
{
     
    int T=4;
    int n=30;
    w[1]=15;
    w[2]=10;
    w[3]=12;
    w[4]=8;
    num[1]=12;
    num[2]=8;
    num[3]=9;
    num[4]=5;


           for(int k=1;k<=T;k++){
     
                for(int m=0;m<=n;m++){
     
                    if(k==1){
     
                        if(w[k]>m){
     
                            a[k][m]=0;
                        }else{
     
                            a[k][m]=num[k];
                        }
                        continue;
                    }
                    if(w[k]>m){
     
                            a[k][m]=a[k-1][m];
                        }else{
     
                            a[k][m]=max(a[k-1][m-w[k]]+num[k],a[k-1][m]);
                        }
                }
           }
          int temp=n;
           for(int x=T;x>0;x--){
     
                if(a[x][temp]==a[x-1][temp]){
     
                    code[x]=0;
                }else{
     
                    code[x]=1;
                    temp=temp-w[x];
                }
           }
       char CHAR ='A';
           for(int ii=1;ii<=T;ii++){
     
                if(code[ii]){
     
                     printf("%c ",CHAR+ii-1);;
                }

           }
           printf("\n");

   return 0;
}

问题 F: 图书排序

某图书销售管理系统需要对图书(Book)进行排序，每一本图书包含书名(bookName)、销量(bookSales)、价格(bookPrice)等属性，要求先按照销量由大到小排序，对于销量相同的图书再按照价格由小到大排序。
输入
每组输入包括两个部分，第一部分为书的数量n，
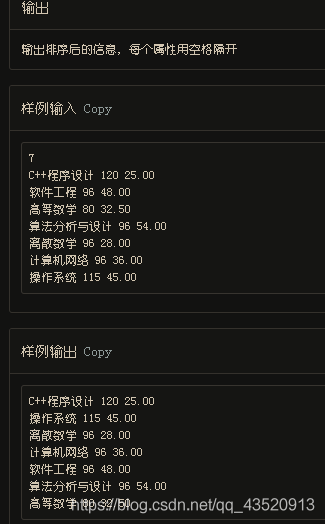
接下来n行则为n本书的信息。 按顺序输入书名(不超过20个字)、销量、价格。
输出
输出排序后的信息，每个属性用空格隔开

#include
 
#define ll long long
const int N=1005;
using namespace std;
 
 
typedef struct {
     
    string name;
    int num;
    double price;
    }Node;
Node node[N];
    bool cmp(Node& a,Node& b){
     
        if(a.num!=b.num){
     
            return a.num>b.num;
        }else{
     
            return a.price<b.price;
        }
    }
int main()
{
     
    int T;
    while(cin>>T){
     
 
        for(int i=1;i<=T;i++){
     
            cin>>node[i].name>>node[i].num>>node[i].price;
        }
 
        sort(node+1,node +T+1,cmp);
        for(int j=1;j<=T;j++){
     
           cout<<node[j].name<<" "<<node[j].num<<" ";
           printf("%.2lf\n",node[j].price);
        }
    }
 
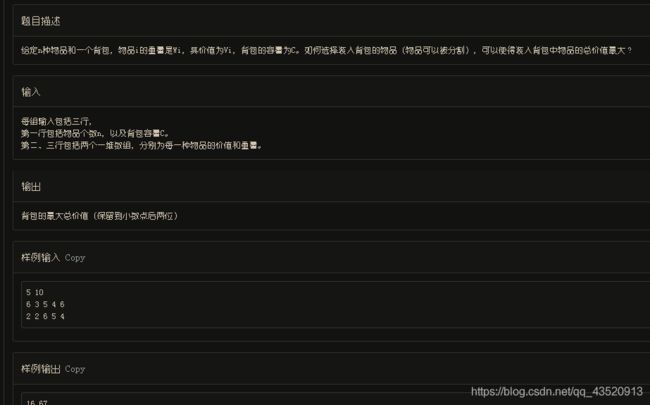
   return 0;
}

问题 G: 部分背包问题

#include

#define ll long long
const int N=1005;
using namespace std;

typedef struct {
     
    int w;
    int v;
    double price;
    }Node;
Node node[N];
    bool cmp(Node& a,Node& b){
     
       return a.price>b.price;
    }
int main()
{
     
    int T,c;
    double last=0.0;
    while(cin>>T>>c){
     

        for(int i=1;i<=T;i++){
     
            cin>>node[i].v;
        }

        for(int k=1;k<=T;k++){
     
            cin>>node[k].w;
            node[k].price=node[k].v*1.0/node[k].w;

        }
        sort(node+1,node +T+1,cmp);
        int j=1;
     while(node[j].w<=c&&j<=T){
     
        last+=node[j].v;
        c-=node[j].w;
        j++;

     }
     if(c>0&&j<=T){
     
        last+=node[j].price*c;

     }
     printf("%.2lf\n",last);
    }

   return 0;
}

问题 H: 汽车加油问题

题目描述
一辆汽车加满油后可以行驶n千米。旅途中有k个加油站。若要使沿途的加油次数最少，请设计一个有效的算法。

输入
第一行有2个正整数n和k，表示汽车加满油后可行驶nkm，且旅途中有k个加油站。接下来1行中，有k+1个整数，表示第k个加油站与第k-1个加油站之间的距离。第0个加油站表示出发地，汽车已加满油，且在第0个加油站满油不算加油，第k+1个加油站表示目的地。(请处理到文件尾)

输出
最少加油次数。如果无法到达目的地，则输出“No Solution”。

#include

#define ll long long
const int N=1005;
#include
using namespace std;
int coun;
int s;
int a[N];
int main(){
     
	int n,k;
	while(cin>>n>>k){
     

		for(int i=0;i<k+1;i++){
     
		cin>>a[i];

		}

	int x=0;
	for(int i=0;i<=k;i++){
     
		if(a[i]>n){
     
			cout<<"No Solution"<<endl;
		x++;
		break;
		}
	}
	if(x!=0)
    	break;
    coun=0;
     s=0;
	for(int i=0;i<=k;i++){
     
		s=s+a[i];
		if(s>n){
     
			coun++;
			s=a[i];
		}
	}
	cout<<coun<<endl;


}

}