LeetCode题解——广度优先搜索(BFS)
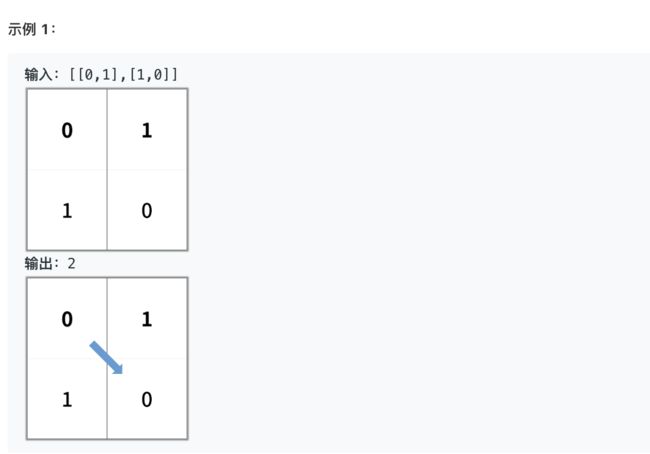
75. 颜色分类
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
注意:
不能使用代码库中的排序函数来解决这道题。
示例:
输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
进阶:
一个直观的解决方案是使用计数排序的两趟扫描算法。
首先,迭代计算出0、1 和 2 元素的个数,然后按照0、1、2的排序,重写当前数组。
你能想出一个仅使用常数空间的一趟扫描算法吗?
直接解决
class Solution {
public:
void sortColors(vector<int>& nums) {
vector<int> v(3);
for(int i = 0; i < nums.size(); ++i)
v[nums[i]]++;
vector<int>::iterator n1 = nums.begin();
for(int j = 0; j < 3; ++j)
for(int i = 0; i < v[j]; ++i)
*n1++ = j;
}
};
一次遍历
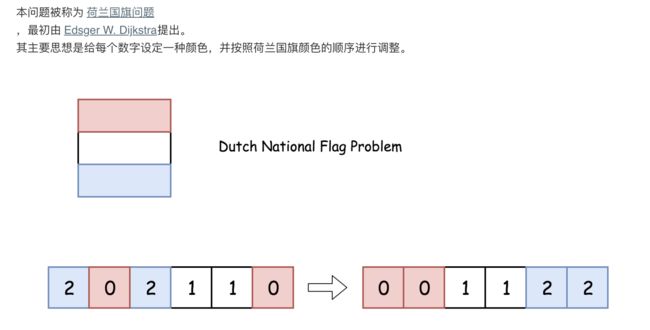
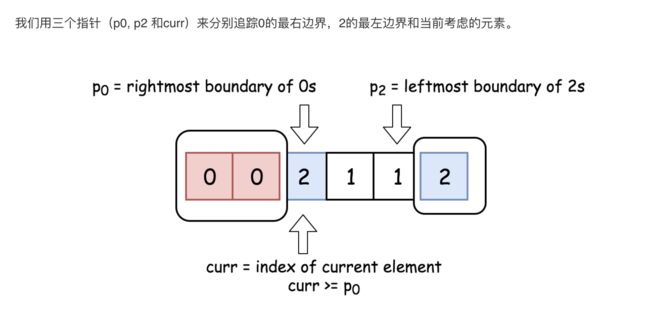
本解法的思路是沿着数组移动 curr 指针,若nums[curr] = 0,则将其与 nums[p0]互换;若 nums[curr] = 2 ,则与 nums[p2]互换。
算法
初始化0的最右边界:p0 = 0。在整个算法执行过程中 nums[idx < p0] = 0.
初始化2的最左边界 :p2 = n - 1。在整个算法执行过程中 nums[idx > p2] = 2.
初始化当前考虑的元素序号 :curr = 0.
While curr <= p2 :
若 nums[curr] = 0 :交换第 curr个 和 第p0个 元素,并将指针都向右移。
若 nums[curr] = 2 :交换第 curr个和第 p2个元素,并将 p2指针左移 。
若 nums[curr] = 1 :将指针curr右移。
class Solution {
public void sortColors(int[] nums) {
int p1 = 0, p2 = nums.length - 1, cur = 0;
while(cur <= p2){
if(nums[cur] == 1){
cur++;
}else if(nums[cur] == 0){
int tmp = nums[p1];
nums[p1++] = nums[cur];
nums[cur++] = tmp;
}else{
int tmp = nums[p2];
nums[p2--] = nums[cur];
nums[cur] = tmp;
}
}
}
}
1091. 二进制矩阵中的最短路径
在一个 N × N 的方形网格中,每个单元格有两种状态:空(0)或者阻塞(1)。
一条从左上角到右下角、长度为 k 的畅通路径,由满足下述条件的单元格 C_1, C_2, …, C_k 组成:
相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通(此时,C_i 和 C_{i+1} 不同且共享边或角)
C_1 位于 (0, 0)(即,值为 grid[0][0])
C_k 位于 (N-1, N-1)(即,值为 grid[N-1][N-1])
如果 C_i 位于 (r, c),则 grid[r][c] 为空(即,grid[r][c] == 0)
返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径,返回 -1 。
BFS
class Solution {
public int shortestPathBinaryMatrix(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] state = new int[m][n];
Deque<Integer> queue = new LinkedList<Integer>();
if(grid[0][0] == 1)
return -1;
if(grid[0][0] == 0 && m == 1 && n == 1)
return 1;
state[0][0] = 1;
queue.addLast(0);
int direction[][] = {
{
0,1},{
1,0},{
0,-1},{
-1,0},{
1,1},{
-1,-1},{
1,-1},{
-1,1}};
while(queue.size() != 0){
int tmp = queue.removeFirst();
int row = tmp / m;
int col = tmp % m;
for(int i = 0; i < direction.length; ++i){
int new_row = row + direction[i][0];
int new_col = col + direction[i][1];
if(new_row >= 0 && new_row < m && new_col >= 0 && new_col < n && grid[new_row][new_col] == 0 && state[new_row][new_col] == 0){
state[new_row][new_col] = state[row][col] + 1;
queue.addLast(m * new_row + new_col);
if(new_row == n - 1 && new_col == n - 1){
return state[new_row][new_col];
}
}
}
}
return -1;
}
}
279. 完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.
动态规划
首先初始化长度为n+1的数组dp,每个位置都为0
如果n为0,则结果为0
对数组进行遍历,下标为i,每次都将当前数字先更新为最大的结果,即dp[i]=i,比如i=4,最坏结果为4=1+1+1+1即为4个数字
动态转移方程为:dp[i] = MIN(dp[i], dp[i - j * j] + 1),i表示当前数字,jj表示平方数
时间复杂度:O(nsqrt(n)),sqrt为平方根
class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1];
for(int i = 1; i <= n; ++i){
dp[i] = i;
for(int j = 1; i - j * j >= 0; ++j){
dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
}
}
return dp[n];
}
}
BFS
import javafx.util.Pair;
class Solution {
public int numSquares(int n) {
if(n == 0)
return 0;
LinkedList<Pair<Integer, Integer> > queue = new LinkedList<>();
queue.addLast(new Pair<>(n, 0));
boolean[] visited = new boolean[n + 1];
visited[n] = true;
while(!queue.isEmpty()){
Pair<Integer, Integer> front = queue.removeFirst();
int num = front.getKey();
int step = front.getValue();
if(num == 0){
return step;
}
for(int i = 1; num - i * i >= 0; ++i){
int a = num - i * i;
if(!visited[a]){
if(a == 0)
return step + 1;
queue.addLast(new Pair(a, step + 1));
visited[a] = true;
}
}
}
return -1;
}
}