哈希及离散化学习笔记
哈希概念
散列函数,又称散列算法、哈希函数,是一种从任何一种数据中创建小的数字“指纹”的方法。 散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。
散列表,也叫哈希表,是根据键(Key)而直接访问在内存存储位置的数据结构。
哈希——通过一种计算使得范围较大的数据对应(映射)到一个较小的范围中,计算得到的就是键值
哈希函数——某一种计算方式(函数)
哈希表——存储数据的数据结构。
碰撞(冲突)—— key1!=key2 但是Hash(key1) = Hash(key2)
哈希表要避免出现碰撞
哈希表
引入
数组的最大特点就是:寻址容易,插入和删除困难;而链表正好相反,寻址困难,而插入和删除操作容易。
那么如果能够结合两者的优点,做出一种寻址、插入和删除操作同样快速容易的数据结构,那该有多好。而这就是哈希表创建的基本思想。
哈希表就是这样一个集查找、插入和删除操作于一身的数据结构。
实现
如果要对1到1e10的数进行哈希,那么显然会内存爆炸
可以考虑对数据进行取模,数组倒是可以存下了,但是这个时候出现了另一个问题,也就是发生碰撞的可能变大
假设取模后的数从0到p,开一个p+1大小的数组
将每个数据一一连接到取模后的数后面,这样查找就可以先确定取模后的地方,再在后面相连的数据里面进行比对
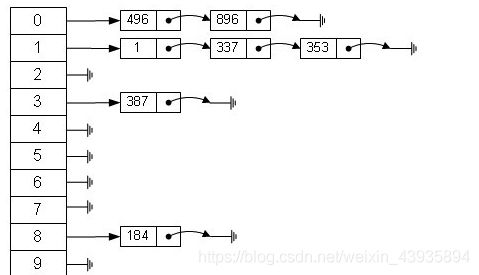
这个方法就叫做开散列法(拉链法)
这种避免冲突最常用的方法表现在构建哈希表上就体现在链表与数组的结合上
取模就是一种定址方法,常见的还有直接定址,平方法等
取模常用较大的素数,最好是2n相关的数,取模速度快
有时候也会使用 & 来计算
例题
方程
考虑具有以下形式的方程:
a * x12 + b * x2 2 + c * x32 + d * x4 2 = 0
a,b,c,d是来自区间[-50,50]的整数和它们中的任何不能为0。
这是考虑的溶液的系统(X1,X2,X3,X4),其验证方程,xi是从[-100,100]和XI的整数!= 0,任意i∈{1, 2,3,4}。
确定满足给定方程的解决方案数量。
分析
1. 我们可以通过直接暴力求解来解决这个问题,通过枚举x1,x2,x3,来确定x4的个数
代码实现
for(int x1=1; x1<=100; ++x1)
for(int x2=1; x2<=100; ++x2)
for(int x3=1; x3<=100; ++x3)
{
int p = -(a*x1*x1+b*x2*x2+c*x3*x3);
if( p%d==0 && p/d>0 && p/d<=10000 && vis[p/d]) ++cnt;
}
2. 通过使用STL库中的map实现算法
代码实现
for(int x1=1; x1<=100; ++x1)
for(int x2=1; x2<=100; ++x2)
cnt[-(a*x1*x1+b*x2*x2)]++;
for(int x3=1; x3<=100; ++x3)
for(int x4=1; x4<=100; ++x4)
if(cnt.count(c*x3*x3+d*x4*x4))
ans+=cnt[c*x3*x3+d*x4*x4];
3. 通过哈希表实现
代码实现
for (int x1 = 1; x1 <= 100; x1++)
{
for (int x2 = 1; x2 <= 100; x2++)
{
insert(-a * x1 * x1 - b * x2 * x2);
}
}
for (int x3 = 1; x3 <= 100; x3++)
{
for (int x4 = 1; x4 <= 100; x4++)
{
ans += search(c * x3 * x3 + d * x4 * x4);
}
}
题解:
#include
#include
#include
#include
using namespace std;
const int N=1e5+10;
const int mod = (1 << 15) - 1;
int head[N];
struct math
{
int v,cnt,next; // v记录值,cnt记录其出现次数,next记录下一个链表的位置
}has[N];
int num,ans;
int Hash(int x)
{
return ((x%mod)+mod)%mod;//获得该数的取模
}
void Insert(int x) //插入操作
{
int y=Hash(x);//引用Hash函数
for(int i=head[y];i!=0;i=has[i].next) //通过head数组遍历链表
{
if(has[i].v==x) //当存在值重复时该数的个数加一
{
has[i].cnt++;
return ;
}
}
has[num].v=x; //当不存在值重复时延长链表
has[num].cnt=1;
has[num].next=head[y];
head[y]=num++;
}
int Search(int x)
{
int y=Hash(x);
for(int i=head[y];i!=0;i=has[i].next) //遍历链表
{
if(x==has[i].v) return has[i].cnt;//当找到数值时,输出其个数
}
return 0;
}
void Flush()
{
num=1;
ans=0;
memset(head,0,sizeof(head));
}
int main()
{
int a,b,c,d;
while(~scanf("%d%d%d%d",&a,&b,&c,&d))
{
if((a>0 && b>0 && c>0 && d>0)||(a<0 && b<0 && c<0 && d<0) )
{
printf("0\n");
continue;
}
Flush();
for(int x1=1;x1<=100;x1++)
for(int x2=1;x2<=100;x2++)
Insert(-(a*x1*x1+b*x2*x2));
for(int x3=1;x3<=100;x3++)
for(int x4=1;x4<=100;x4++)
ans+=Search((x3*x3*c+d*x4*x4));
printf("%d\n",ans*16);
}
return 0;
}
字符串哈希
要把字符串转换为一个整数,可以直接使用ASCII码的字母键值来对应每个字母
最简单的转换:相加
但是这种方式极其容易发生碰撞,比如 a + d = b + c
可以想到用乘系数的方式来减少发生碰撞的几率
用系数的n次方作为每个字符的系数
计算哈希值:
Hash[ i ] = (Hash[ i-1 ] * seed + s[ i ]) % mod
Hash( t )= (Hash( s+t ) - seed^length(t) *Hash(s) ) % mod
通常我们取mod为 264 或 232,也就是直接用
unsigned long long 或 unsigned int类型来存储,计算时自动取模,避免低效的取模运算
seed
奇数? 偶数?
质数?
通常取2^n-1 ,因为计算机二进制运算更快
更通常来说,一般取31,131,1313
一般我们认为这种条件下不会发生碰撞
例题
给定一个字符串A和一个字符串B,求B在A中的出现次数。A和B中的字符均为英语大写字母或小写字母。A中不同位置出现的B可重叠。
思路:
1.计算字符串每个位置的系数
f[0] = 1;
for (int i = 1; i < maxn; i++)
f[i] = f[i - 1] * temp;
2.计算字符串a的哈希值
for (int i = 1; i <= la; i++) {
Hash[i] = Hash[i - 1] * temp + (a[i - 1] - 'a' + 1);
}
3.计算字符串b的哈希值
for (int i = 0; i < lb; i++) {
hb = hb * temp + (b[i] - 'a' + 1);
}
4.查询
for (int i = lb; i <= la; i++) {
if (Hash[i] - Hash[i - lb] * f[lb] == hb)
ans++;
}
对每个位置进行比较,若哈希值相等,则认为字符串相同
代码实现
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
const int mod = (1 << 15) - 1;
const int hasht=31;
ll Hash[N];
ll f[N];
int ans;
ll hd;
string a,b;
int main()
{
cin>>a>>b;
int al=a.length();
int bl=b.length();
f[0]=1;
for(int i=1;i 双哈希
typedef pair pll;
map mapp;
const pll init = {0, 0}, temp = {31, 131};
有些题会卡map的映射,可以考虑用数组加二分(lower_bound),哈希表等
例题
[BeiJing2011]矩阵模板
给定一个M行N列的01矩阵,以及Q个A行B列的01矩阵,你需要求出这Q个矩阵哪些在原矩阵中出现过。 所谓01矩阵,就是矩阵中所有元素不是0就是1。
对于100%的数据,N,M<=1000 A,B<=100
思路
Hash[ i ] = (Hash[ i-1 ] * seed + s[ i ]) % mod
首先对每一行哈希
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++)
Hash[i][j] += Hash[i][j - 1] * seed1 + s[i][j] ; }
这时二维数组就变成了一个一维数组,继续进行哈希
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++)
Hash[i][j] += Hash[i - 1][j] * seed2; }
首先我们先了解一下二维前缀和
从一维前缀和开始 假设数组sum为数组a的前缀和,即sum[ n ]为数组a 1到n的和 那么二维前缀和sum[ i ][ j
]就是从(1,1)到(i,j)的所有数字的和 那么对每个i, sum[ i ]-sum[ i-1 ]=a[ i ]
sum[ i ]-sum[ i-2 ]=a[ i ]+a[ i-1 ]
…………
sum[ i ]-sum[ i-k ]=a[ i ] + …… +a[ i-k+1 ]
对a*b的矩阵
ans[ a ][ b ] =sum[ i ][ j ] – sum[ i - a ][ j ] – sum[ i ][ j - b ] + sum[ i - a ][ j –b ]
计算一个矩阵里a*b的小矩阵的哈希值
ans = Hash[i][j]-Hash[i - a][j] * f2[a] - Hash[i][j - b]* f1[b] + Hash[i - a][j - b] * f1[b] * f2[a]
进行查找输出结果
代码实现
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=1e3+10;
const int mod = 1e9+7;
const int seed1=31; //行哈希seed
const int seed2=131; //列哈希seed
ll f1[N],f2[N];
ll Hash[N][N];
char s1[N][N],s2[N][N];
int data[N*N];
ll CalHash(int a,int b)
{
ll ans=0;
for(int i=1;i<=a;i++)
{
ll temp=0;
for(int k=1;k<=b;k++)
temp=temp*seed1+(s2[i][k]-'0');
ans=ans*seed2+temp;
}
return ans%mod;
}
void Flush()
{
f1[0]=1,f2[0]=1;
for(int i=1;i<120;i++)
{
f1[i]=f1[i-1]*seed1; // 初始化 行哈希数组f1 列哈希数组 f2
f2[i]=f2[i-1]*seed2;
}
}
int main()
{
int n,m,a,b,cnt=0;
scanf("%d%d%d%d",&n,&m,&a,&b);
Flush();
for(int i=1;i<=n;i++) scanf("%s",s1[i]+1);
for(int i=1;i<=n;i++)
for(int k=1;k<=m;k++)
Hash[i][k]+=Hash[i][k-1]*seed1+(s1[i][k]-'0'); //对每一行哈希求前缀和
for(int i=1;i<=n;i++)
for(int k=1;k<=m;k++)
Hash[i][k]+=Hash[i-1][k]*seed2; // 对每一列哈希求前缀和
for(int i=a;i<=n;i++)
for(int k=b;k<=m;k++) //计算矩阵中每一个a*b矩阵的哈希值
{
ll temp=Hash[i][k]-Hash[i-a][k]*f2[a]-Hash[i][k-b]*f1[b]+Hash[i-a][k-b]*f2[a]*f1[b];
data[cnt++]=(int)(temp%mod); // 用data数组储存每一个矩阵哈希值
}
sort(data,data+cnt); //sort函数整理data数组
int ques;
scanf("%d",&ques);
while(ques--)
{
for(int i=1;i<=a;i++) scanf("%s",s2[i]+1);
int ha=(int)CalHash(a,b)%mod; //获得每一问中a*b矩阵的哈希值
if(data[lower_bound(data,data+cnt,ha)-data]==ha) printf("1\n"); //二分查找
else printf("0\n");
}
return 0;
}
离散化
当数据范围很大数量却不多,并且关注的不是数值本身,而是数据之间的顺序,出现次数等与数值本身大小无关的信息时,通常采用离散化的方法处理数据
设有4个数:1234567、123456789、12345678、123456排序:123456<1234567<12345678<123456789
=> 1 < 2 < 3 < 4
那么这4个数可以表示成:2、4、3、1
一般常见两种方法
第一种 使用STL a数组与b数组存的值相同
sort(a, a+n);
int size=unique(a, a+n)-a; //size为离散化后元素个数
for(i=0;i若离散化后序列为0, 1, 2, …, size - 1则用lower_bound,从1, 2, 3, …, size则用upper_bound,其中lower_bound返回第1个不小于b[i]的值的指针,而upper_bound返回第1个大于b[i]的值的指针,当然在这个题中也可以用lower_bound然后再加1得到与upper_bound相同结果,两者都是针对以排好序列。
第二种
struct node
{
int a,p;
}s[maxx];
bool cmp(node x,node y){
if(x.a==y.a) return x.p>s[i].a;
s[i].p=i;
}
sort(s+1,s+n+1,cmp);
for(int i=1; i<=n; i++)
b[s[i].p]=i;