ACM-ICPC 2018 徐州赛区网络预赛G （单调队列）

传送门

题面：

There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.

Input

The first line is the number of waves n(n \le 50000)n(n≤50000).

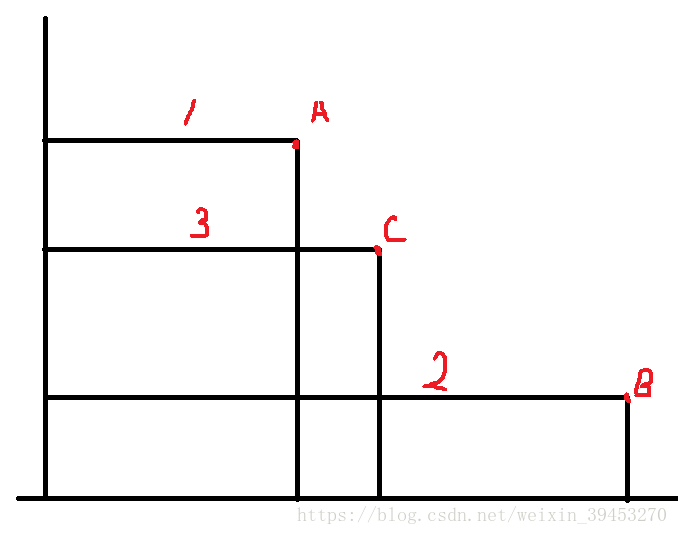
The next nn lines，each contains two numbers xx yy ,( 0 < x0

Output

An Integer stands for the answer.

Hint：

As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10

样例输入复制

3
1 4
4 1
3 3

样例输出复制

10

题目来源

ACM-ICPC 2018 徐州赛区网络预赛

题目描述：

    有nn次涨潮和退潮，每次的范围是个x×yx×y的矩形，求n次涨退潮后，潮水痕迹的长度。 
 不存在此i,j∈[1,n],i≠j,xi≤xj且yi≤yji,j∈[1,n],i≠j,xi≤xj且yi≤yj 

题目分析：

    题目中有一个很重要的条件，就是形成的两个矩阵必定不能两两包含，这个条件就可以省去我们讨论很多情况。

    首先，我们将所有点根据x坐标排序，并根据加入的时间分别给他们打上时间标记，可以得到如下图：

    因为题目中的条件，倘若根据x进行排序，对应的也等价于对y坐标进行排序。我们根据x的大小遍历所有的点，我们可以发现，当前的点i的x坐标对答案的贡献为第1个点到第i个点中标记单调递增的个数size*(xi-xi-1)。y同理。

    因此我们可以考虑用单调队列去维护每一个点对答案答案的贡献。而因为正着维护单调队列比较麻烦，因此我们可以考虑倒着维护单调队列，最后统计答案即可。时间复杂度O（n）。

代码：

#include 
#define maxn 50005
using namespace std;
typedef long long ll;
struct Node{
    ll x,y;
    int id,a,b;
    bool operator<(const Node &b){
        return xque;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld%lld",&q[i].x,&q[i].y);
        q[i].id=i;
    }
    sort(q+1,q+1+n);
    for(int i=1;i<=n;i++){//因为y的答案是从n开始统计的故此要从1开始维护答案
        while(!que.empty()&&q[i].id>que.back()) que.pop_back();
        que.push_back(q[i].id);
        q[i].a=que.size();
    }
    que=deque();
    for(int i=n;i>=1;i--){//倒着统计x的答案
        while(!que.empty()&&q[i].id>que.back()) que.pop_back();
        que.push_back(q[i].id);
        q[i].b=que.size();
    }
    ll res=0,xx=0,yy=0;
    for(int i=1;i<=n;i++){//统计x的答案
        res+=(q[i].x-xx)*q[i].b;
        xx=q[i].x;
    }
    for(int i=n;i>=1;i--){//统计y的答案
        res+=(q[i].y-yy)*q[i].a;
        yy=q[i].y;
    }
    printf("%lld\n",res);
    return 0;
}

 

转载于:https://www.cnblogs.com/Chen-Jr/p/11007196.html