FPGA图像处理9_常用算法_直方图均衡
直方图均衡
直方图均衡算法通过将各颜色通道的像素点数值间距拉大,实现在当前颜色通道内像素点数值的大幅差异,增强视觉效果。除此以外,在图像传感器输入的像素值位宽与实际用于显示的像素值位宽不一致的情况下,直方图均衡算法也常用于像素点位宽的转换。
对于 RGB 图像,可以先将其转化为 YUV 图像,仅对 Y 通道执行直方图均衡算法后,再由 YUV 图像转化为 RGB 图像,实现彩色图像的增强。
一般情况下直方图均衡用于灰度图像。
以像素值位宽 8 为例,说明直方图均衡算法。
定义直方图数组为 hist[256](28=256),每个数组元素的数值表示当前图像帧内灰度值等于其序号的像素点的个数。
设当前像素值为 x,经过直方图均衡计算后输出的像素值为 y,一帧图像内的像素点总数为 N,则有以下公式:
y = ( 2 8 − 1 ) × ∑ k = 0 x h i s t [ k ] N y=(2^8-1)\times \frac{\sum^{x}_{k=0}{hist[k]}}{N} y=(28−1)×N∑k=0xhist[k]
对上述公式的解释:小于等于当前像素值的点的数目在整帧所有像素点中所占比例,即为该像素值的增强输出值与满量程的比值。
设当前图像所有像素点的最小值为 min,则其对应的输出值为 0,因为没有比 min 值更小的像素值输入。
设当前图像所有像素点的最大值为 max,则其对应的输出值为 2 8 − 1 2^8-1 28−1,因为所有像素点都小于或者等于 max。
注意:
- (28-1) 指的是输出像素点的满量程值,如果输入输出像素值位宽不同,若输出位宽为 P,则 (28-1) 用 (2P-1) 替换。
- hist[256] 中的 256 源于输入像素点的可能值范围,即 0 至 255,若输入位宽为 Q,则 hist[256] 用 hist[2Q] 替换。
根据计算公式,可以发现直方图均衡算法的计算复杂度较低,而在逻辑处理上较为复杂,因此比较适合使用 Verilog 语言而不是 sysgen 实现。
在 FPGA 实现中,首先需要改变直方图统计的算法,因为直方图数值 hist 本身不参与计算,参与计算的是 ∑ k = 0 x h i s t [ k ] \sum^x_{k=0}{hist[k]} ∑k=0xhist[k],因此在数据输入过程中直接统计计算 ∑ \sum ∑ 数值。
除了直方图统计方法外,另一个特殊处理是用前一帧图像的直方图统计结果计算当前图像帧的直方图均衡。
因为,直方图统计算法只有收到当前图像的全部数据后才能得到结果,接收当前帧全部数据后再执行直方图均衡计算一方面需要对当前图像帧数据进行一帧的缓冲,另一方面需要至少等待一帧图像数据的传输时间才能启动运算。由于前后2帧图像之间具有一定的连续性,变化差异不至于太大,计算产生的误差是可以接受的,用前一帧的直方图统计结果可以直接在当前图像帧数据的输入流水线中计算。
为了实现这种处理,需要同时进行直方图均衡计算和直方图统计 2 种计算。因此采用 ping/pong 切换的方法控制两个直方图统计数组进行循环切换。即使用 ping 组用于计算的时候,用 pong 组进行统计;使用 pong 组计算的时候,用 ping 组进行统计。
最后在直方图均衡计算中 × 2 8 − 1 N \times\frac{2^8-1}{N} ×N28−1的计算,根据具体数值选择乘以整数常数后除以 2 的指数,除法用截去低位的办法实现。
计算过程中还有一点需要注意的是,由于使能前一帧的统计结果用于当前帧的计算,帧间差异以及计算误差可能产生小于 0 或者大于满量程的均衡计算结果,需要在计算过程中进行判断并且做饱和处理。
直方图统计的 Verilog 代码可参考以下:
//用ping/pong切换方式写入hist数组,防止更新数值的同时进行读出
//计算直方图增强时使用前一帧的统计值
//注意下方hist并非实际直方图,而是直方图累加值
//累加最大值为640*480=307200,共19位
reg [18:0] hist_ping[255:0];//输入Gray数值位宽为8
reg [18:0] hist_pong[255:0];
genvar i;
generate
for (i=0; i < 256; i=i+1)
begin: hist_gen
always @(posedge clk) begin
case ({fv_d1, in_fv, hist_flag})
{1'b1, 1'b0, 1'b0}: begin//用输入fv的下降沿复位hist
//hist_flag下个时钟周期将切换至pong写入,因此复位pong
hist_pong[i] <= 19'd0;
//ping保持
hist_ping[i] <= hist_ping[i];
end
{1'b1, 1'b0, 1'b1}: begin//用输入fv的下降沿复位hist
//hist_flag下个时钟周期将切换至ping写入,因此复位ping
hist_ping[i] <= 19'd0;
//pong保持
hist_pong[i] <= hist_pong[i];
end
default: begin//直方图累加计算
case ({in_fv, in_lv, hist_flag})
{1'b1, 1'b1, 1'b0}: begin//写入ping
if (in_gray <= i) begin
//累加Gray值小于当前序号i的像素点
hist_ping[i] <= hist_ping[i]+19'd1;
end
else begin
//当前像素点Gray值大于i,保持
hist_ping[i] <= hist_ping[i];
end
//pong保持
hist_pong[i] <= hist_pong[i];
end
{1'b1, 1'b1, 1'b1}: begin//写入pong
if (in_gray <= i) begin
//累加Gray值小于当前序号i的像素点
hist_pong[i] <= hist_pong[i]+19'd1;
end
else begin
//当前像素点Gray值大于i,保持
hist_pong[i] <= hist_pong[i];
end
//ping保持
hist_ping[i] <= hist_ping[i];
end
default: begin
hist_ping[i] <= hist_ping[i];
hist_pong[i] <= hist_pong[i];
end
endcase
end
endcase
end
end
endgenerate
最大值最小值的统计与直方图统计一样使用 ping/pong 切换的方式统计:
//统计帧最大值和最小值,ping/pong切换与直方图数据一致
reg [7:0] max_ping = 8'h00;
reg [7:0] min_ping = 8'hFF;
reg [7:0] max_pong = 8'h00;
reg [7:0] min_pong = 8'hFF;
always @(posedge clk) begin
case ({fv_d1, in_fv, hist_flag})
{1'b1, 1'b0, 1'b0}: begin//fv下降沿复位max/min
//下个时钟周期切换至pong,当前复位pong
max_pong <= 8'h00;
min_pong <= 8'hFF;
//ping保持
max_ping <= max_ping;
min_ping <= min_ping;
end
{1'b1, 1'b0, 1'b1}: begin//fv下降沿复位max/min
//下个时钟周期切换至ping,当前复位ping
max_ping <= 8'h00;
min_ping <= 8'hFF;
//pong保持
max_pong <= max_pong;
min_pong <= min_pong;
end
default: begin//记录max/min值
case ({in_fv, in_lv, hist_flag})
{1'b1, 1'b1, 1'b0}: begin//写入ping
//记录max
if (in_gray > max_ping) begin
max_ping <= in_gray;
end
else begin
max_ping <= max_ping;
end
//记录min
if (in_gray < min_ping) begin
min_ping <= in_gray;
end
else begin
min_ping <= min_ping;
end
//pong保持
max_pong <= max_pong;
min_pong <= min_pong;
end
{1'b1, 1'b1, 1'b1}: begin//写入pong
//记录max
if (in_gray > max_pong) begin
max_pong <= in_gray;
end
else begin
max_pong <= max_pong;
end
//记录min
if (in_gray < min_pong) begin
min_pong <= in_gray;
end
else begin
min_pong <= min_pong;
end
//ping保持
max_ping <= max_ping;
min_ping <= min_ping;
end
default: begin
//ping保持
max_ping <= max_ping;
min_ping <= min_ping;
//pong保持
max_pong <= max_pong;
min_pong <= min_pong;
end
endcase
end
endcase
end
根据当前输入的像素值选择直方图统计数值:
//直方图数组输出
reg [18:0] out_hist = 19'd0;
always @(posedge clk) begin
case (hist_flag)
1'b0: begin//当前读出pong
if (in_gray > max_pong) begin
//当前Gray值大于最大值,则按最大值输出
out_hist <= hist_pong[max_pong];
end
else if (in_gray < min_pong) begin
//当前Gray值小于最小值,则按最小值输出
out_hist <= hist_pong[min_pong];
end
else begin
//按当前Gray值输出
out_hist <= hist_pong[in_gray];
end
end
1'b1: begin//当前读出ping
if (in_gray > max_ping) begin
//当前Gray值大于最大值,则按最大值输出
out_hist <= hist_ping[max_ping];
end
else if (in_gray < min_ping) begin
//当前Gray值小于最小值,则按最小值输出
out_hist <= hist_ping[min_ping];
end
else begin
//按当前Gray值输出
out_hist <= hist_ping[in_gray];
end
end
endcase
end
自适应直方图均衡
自适应直方图均衡算法与普通均衡算法的不同点在于它通过计算图像多个局部区域的直方图,重新分布亮度,以此增强图像显示效果,该算法更适合于提高图像的局部对比度和细节部分。
如果图像中包括明显亮的或者暗的区域,普通直方图均衡算法可能会造成这些区域的细节丢失,而自适应直方图均衡算法则可以将这些区域的图像细节进行增强。
自适应直方图均衡的算法首先将图像分为若干互不重叠的图像子块,在图像子块中按照与普通均衡算法。
相同的方式进行直方图统计,得到子块中各输入像素值对应的输出像素值。
由于各图像子块间直方图分布不一致,每个子块独立执行普通均衡算法的情况下,在子块边缘处会出现明显的分界线。为解决边缘处的分界线,采用双线性插值的办法。
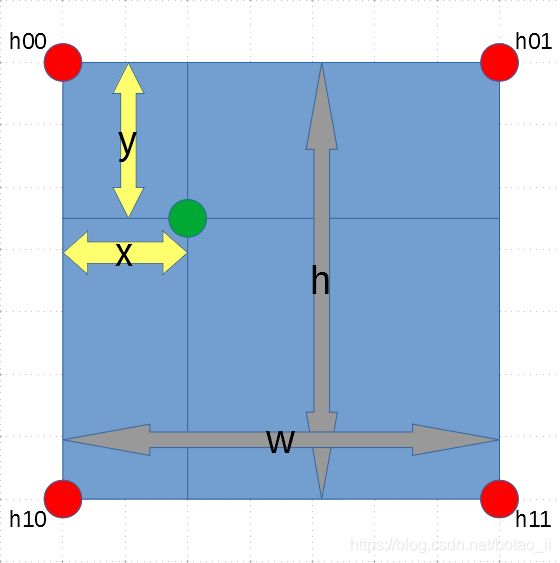
以每个子块中心坐标作为该子块的坐标,首先找到包围当前像素点坐标的 4 个图像子块,当前像素点值在此 4 个子块内的普通均衡算法输出值分别为 h00, h01, h10, h11。
使用双线性插值部分的示意图,即用下图中 4 个红点像素插值计算绿点像素的数值。
双线性插值的部分可以使用 sysgen 实现。
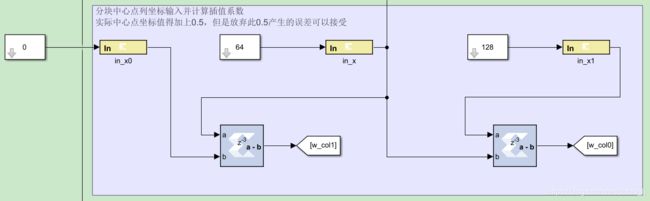
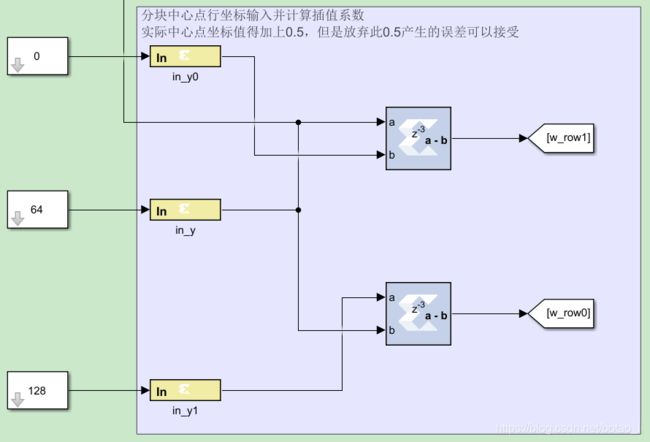
在 sysgen 中定义 h00 的坐标为 (x0, y0),h11 的坐标为 (x1, y1),为方便双线性插值中的除法计算,在原图分块时就设定:
- x1-x0=128
- y1-y0=128
计算列插值系数如下:
计算行插值系数如下:
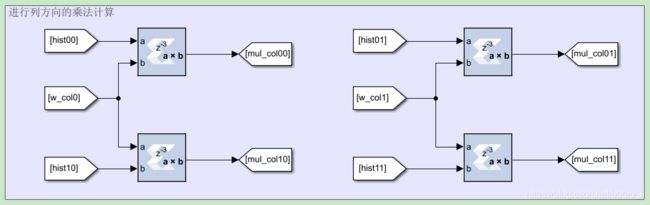
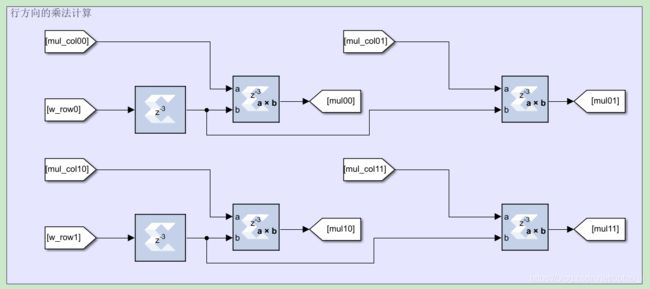
首先进行列方向的插值计算:
之后进行行方向的插值计算:
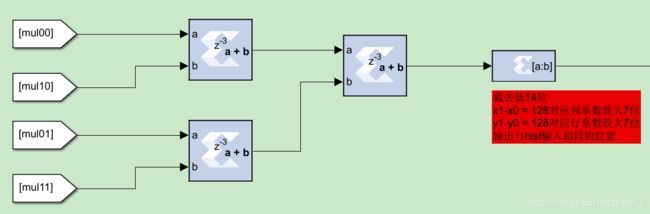
各插值项相加得到双线性插值的结果,注意下图中使用的截去低 14 位实现除法计算:
除了上述的双线性插值计算以外,用 Verilog 实现图像分块的普通直方图均衡计算,每个分块的直方图均衡算法定义为单独的 Verilog 模块,并且由上文所述每个分块大小为 128 × 128 128\times 128 128×128,于是可以将输入像素点行列坐标截去低 7 位后用于判断当前像素点所属的分块。
另外一个处理技巧是判断包围当前像素点的 4 个图像子块。
首先通过当前像素点与其所在分块的中心点的相对位置关系计算 4 个图像子块的序号:
//选择包围当前像素点的4个分块
//每个分块中心点按照分块坐标系而言为(63.5, 63.5)
//以分块中心点将分块分为4个象限
//用当前像素点坐标的低7位判断当前点在其分块中的4个象限
//由于分块为128x128,则分块序号用像素点坐标截去低7位表示
//列坐标判断
//定义4个分块序号(x_ind, y_ind)
reg [8:0] x_ind_00 = 9'd0;
reg [8:0] x_ind_01 = 9'd0;
reg [8:0] x_ind_10 = 9'd0;
reg [8:0] x_ind_11 = 9'd0;
reg [8:0] y_ind_00 = 9'd0;
reg [8:0] y_ind_01 = 9'd0;
reg [8:0] y_ind_10 = 9'd0;
reg [8:0] y_ind_11 = 9'd0;
always @(posedge clk) begin
if (in_x[6:0] < 7'd64) begin
//当前点在分块的左半边
x_ind_00 <= in_x[15:7]-9'd1;
x_ind_10 <= in_x[15:7]-9'd1;
x_ind_01 <= in_x[15:7];
x_ind_11 <= in_x[15:7];
end
else begin
//当前点在分块的右半边
x_ind_00 <= in_x[15:7];
x_ind_10 <= in_x[15:7];
x_ind_01 <= in_x[15:7]+9'd1;
x_ind_11 <= in_x[15:7]+9'd1;
end
end
always @(posedge clk) begin
if (in_y[6:0] < 7'd64) begin
//当前点在分块的上半边
y_ind_00 <= in_y[15:7]-9'd1;
y_ind_01 <= in_y[15:7]-9'd1;
y_ind_10 <= in_y[15:7];
y_ind_11 <= in_y[15:7];
end
else begin
//当前点在分块的下半边
y_ind_00 <= in_y[15:7];
y_ind_01 <= in_y[15:7];
y_ind_10 <= in_y[15:7]+9'd1;
y_ind_11 <= in_y[15:7]+9'd1;
end
end
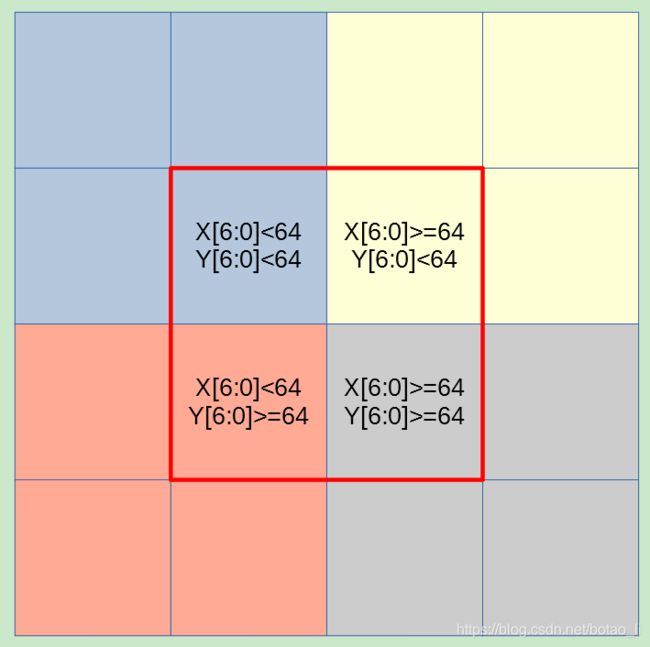
上述代码的原理示意图,红框表示当前像素点所在的图像子块,4 种填充色的 4 角指示包围当前像素点的 4 个子块的中心点:
如果上图中红框表示的当前分块位于整幅图像的边缘,则 4 个填充色很可能有部分位于图像以外,于是需要对边缘进行判断,如下方代码所示:
//定义函数进行边缘控制
//分块列序号边缘控制函数
function [8:0] func_x_ind;
input x_ind;
begin
if (x_ind[8] == 1'b1) begin
//由减9'd1计算得到负值,表示序号小于0,用0值代替
func_x_ind = 9'd0;
end
else if (x_ind[8:0] > 所有分块的最大列序号) begin
//由加9'd1得到序号大于最大值,用最大值代替
func_x_ind = 所有分块的最大列序号;
end
else begin
//序号在有效范围内
func_x_ind = x_ind;
end
end
endfunction
//分块行序号边缘控制函数
function [8:0] func_y_ind;
input y_ind;
begin
if (y_ind[8] == 1'b1) begin
//由减9'd1计算得到负值,表示序号小于0,用0值代替
func_y_ind = 9'd0;
end
else if (y_ind[8:0] > 所有分块的最大行序号) begin
//由加9'd1得到列序号大于最大值,用最大值代替
func_y_ind = 所有分块的最大行序号;
end
else begin
//序号在有效范围内
func_y_ind = y_ind;
end
end
endfunction
//定义4个分块序号(x, y)
//实际用于4分块选择
reg [8:0] x_00 = 9'd0;
reg [8:0] x_01 = 9'd0;
reg [8:0] x_10 = 9'd0;
reg [8:0] x_11 = 9'd0;
reg [8:0] y_00 = 9'd0;
reg [8:0] y_01 = 9'd0;
reg [8:0] y_10 = 9'd0;
reg [8:0] y_11 = 9'd0;
always @(posedge clk) begin
x_00 <= func_x_ind(x_ind_00);
x_01 <= func_x_ind(x_ind_01);
x_10 <= func_x_ind(x_ind_10);
x_11 <= func_x_ind(x_ind_11);
y_00 <= func_y_ind(y_ind_00);
y_01 <= func_y_ind(y_ind_01);
y_10 <= func_y_ind(y_ind_10);
y_11 <= func_y_ind(y_ind_11);
end
仿真结果
下方仿真图像并非上述代码仿真得到,仅用于示意 2 种直方图均衡算法的处理差异。
输入图像为 1280 × 960 1280\times 960 1280×960 分辨率,自适应直方图算法使用 320 × 320 320\times 320 320×320 的分辨率划分 4 × 3 4\times 3 4×3 个图像子块:
试验图片来源于:http://www.netbian.com/
原始图像:
普通直方图均衡输出:
自适应直方图均衡输出: