软件分析笔记——数据流

热烘烘的第三篇来啦！（dbq，我看的太慢了，断断续续拖了好几天才看完了）
这篇文章是B站南大《软件分析》课的第三节、第四节的总和。由于这两节课讲的都是数据流，有连贯性，就一起看做了笔记。
再次要感谢南大的李越老师，讲的真的太仔细、太到位了（之前上类似的课的时候都没有听懂，这次我终于听懂了），我被成功的洗了脑
ps：由于是边听课边记的笔记，可能有语法、语义上面的错误，欢迎大家提出，我会及时修改的。

1. 数据流分析的概述

大概讲数据流分析的概念、考虑的方面。

大致来讲，就是看数据如何在CFG图上面流动。数据要抽象（abstraction），流动要过近似（over-approximate），这是静态分析的两个要点

• 这里的数据是对特定的应用来讲的，所以不同的数据流分析关注不同的数据。
• CFG图主要就是看边（控制流，就是点的流向）和点（就是基本块BBs）

对于大部分的静态分析器，都是may analysis

• may analysis：输出的信息可能是正确的（也有可能是错误的），所以是过近似的分析
• must analysis：输出的信息一定是正确的，所以是欠近似分析

=> 这些都主要是为了分析结果的安全性

总结：不同的数据流分析有不同的数据抽象，也有不同的流近似策略。那么就对应了不同的转换函数和不同的控制流处理方法。

2. 数据流分析的预备知识

主要讲一些形式化的定义、符号等，是基础知识。

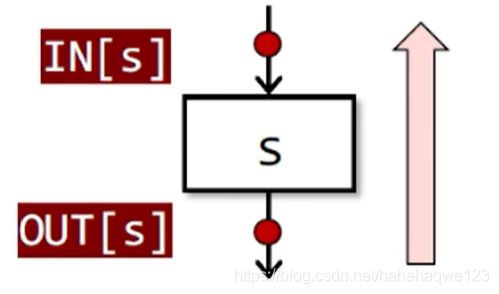
1. IN[s1]、OUT[s2]

   IN[s1]是指执行该语句块之前程序的状态

   OUT[s1]是执行该语句之后程序的状态
   
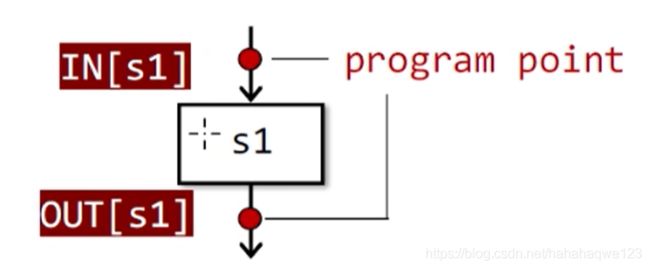
   可以发现规律：在顺序执行时，s1的输出就是下一个程序块s2的输入，即OUT[s1]=IN[s2]
   
   对于分支分叉：每个叉都是OUT[s1]
   
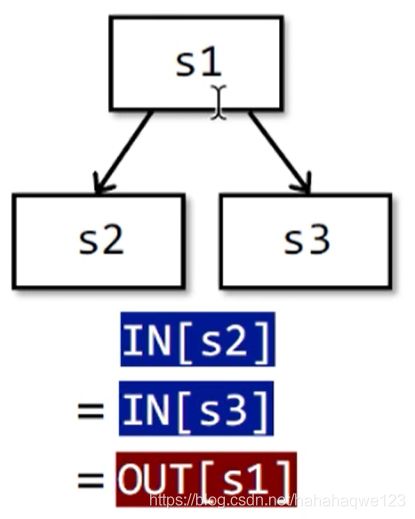
   对于分支汇聚：操作是meet operator（可能是并集、也可能是交集，也可能是其他操作方法）
   

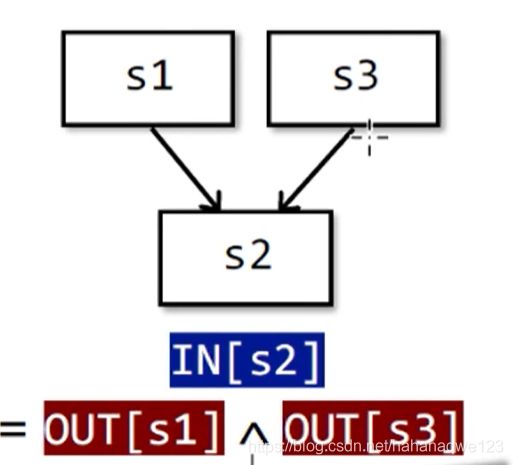
2. program point：程序点，就是每个数据块入口前和出口后的两个点

   在数据流分析应用中，每个程序点的数据流的值都被表示为所有可能程序状态的一个抽象
   
   数据流值的表达范围（就是抽象的符号集合）：被称为值域domain：（例如上图的domain就是如下图）
   
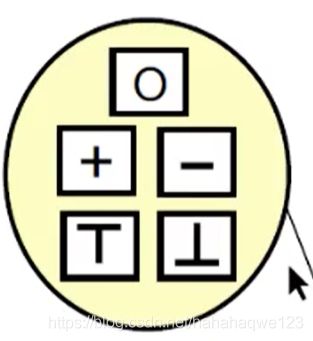
   =>数据流分析，就是对于所有声明的IN[s]和OUT[s]找到安全近似约束下的解???

   而约束的内容是基于转换函数和控制流

3. 转换函数的约束表达和符号

   • 前向分析：$OUT[s]=f_s(IN[s])$
     ps：前向分析是我自己取的名 forward analysis，感觉很不专业
     
   • 反向分析：$IN[s]=f_s[OUT[s]]$
     
     两者可以相互转换：对于反向分析，可以将控制流图反方向画，然后利用正向分析，等同于反向分析

4. 控制流约束的表达和符号

   • 在BB内部的控制流

     前面一个输出就是后面一个的输入，形式化表示就是：$IN[s_{i+1}]=OUT[s_i],i=1,2,...n-1$
     

   • 在BBs之间的控制流

     本质上，BB的输入就是BB中第一个语句的输入，BB的输出就是最后一个语句的输出，形式化定义：$IN[B]=IN[s_1],OUT[B]=OUT[s_n]$

     $OUT[B]=f_B(IN[B]),f_B=f_{s_n}•...f_{s_2}•f_{s_1}$，映射就是每个语句的映射，合起来就是

     $IN[B]={\bigwedge }_{p}OUT[P]$（P是B的一个前驱）。（该句的含义是，所有B的前驱的OUT的meet operator）

     同理，如果是反向分析：就是先分析out后分析in

     $IN[B]=f_B(OUT[B]),f_B=f_{s_1}•...f_{s_{n-1}}•f_{s_n}$

     $IN[B]={\bigwedge }_{S}OUT[S]$。S是B的一个后继
     
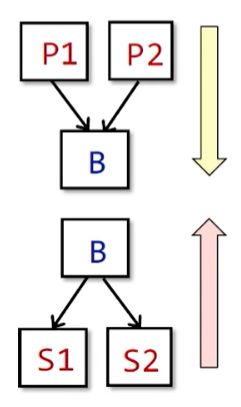
     =>下面的三节，并不考虑函数调用，所有举的例子都是在函数内部的（inter-procedural analysis）

   不考虑别名（两个变量都指向同一个地址），即每个变量都是指向单独一个地址的，每个地址唯一对应一个变量（pointer analysis）

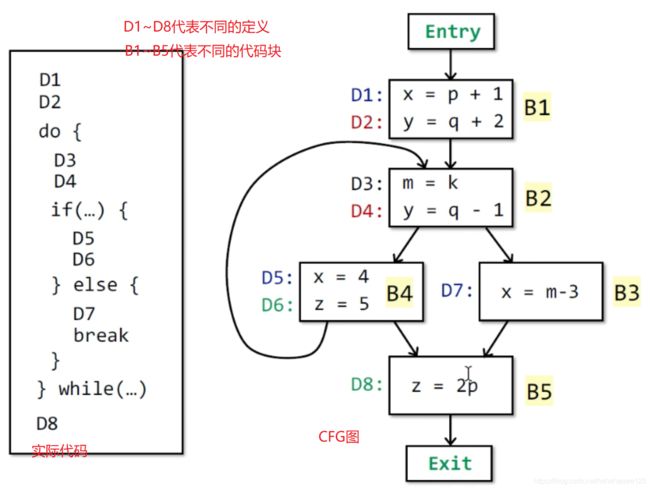
3.可达定义的分析（reaching definition）

主要讲：什么是可达定义，如何理解

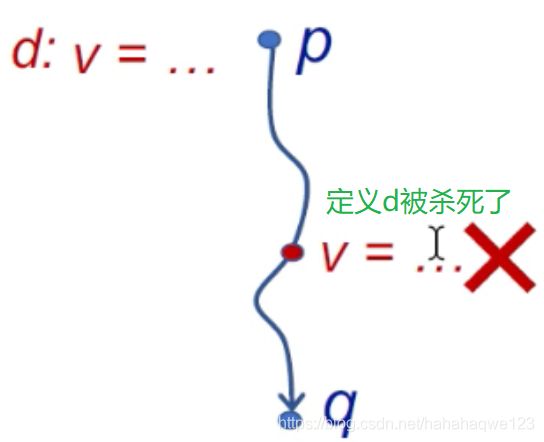
1. 一些命名： 定义d：是一个语句对变量v进行赋值

2. 可达性定义概念：定义d从程序点p到q是可达的：满足存在一条路径从p到q，该路径上d没有被杀死（就是变量没有被重新定义）
   

3. 应用：用来检测未初始化就使用的变量。

   方法：可以在在entry中给每一个变量一个dummy definition（看成假定义），如果从dummy definition能够到达某个程序点，该点在使用变量v

   =>则就能发现该路径上，对变量v未定义就使用 =>这个是may analysis（过近似，因为只考虑部分路径，所以是可能会发生而不是一定会发生）

4. 对可达定义的理解

   • 抽象

     列举出程序中所有的定义，每个定义都用1bit来表示，从而构成一个n位得bit向量
     

   • 近似（安全近似 safe-approximation，不管是must or may，给定的结果去优化程序，但是不能导致程序产生错误，这就是安全优化）

     对于一个语句：D: v = x op y ,它产生了一个关于v的定义，杀死了关于v的其他定义

     • 转换函数

       gen[B]就是BB中被新定义的语句，$kil{l}_B$在BB对应被杀死的
       
       举例：
       

     • 控制流

       $IN[B]={\bigcup }_{PapredecessorofB}OUT[P]$

       就是B的所有前驱结点的OUT的并集（就是meet operator的一个具体实现）
       

5. 可达定义的算法的实现：迭代算法
   
   ps：对于may analysis，初始化一般都为空；must analysis一般都为top（满）

   举例：
   

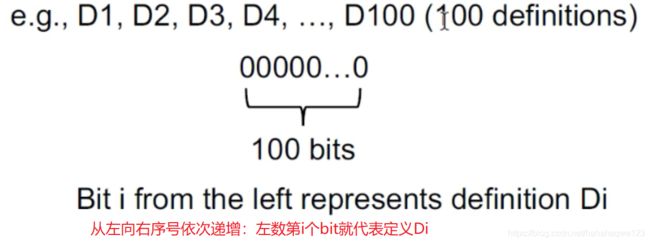
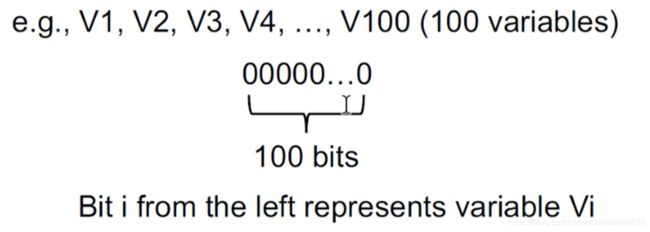
   • 抽象：将每个定义都给一个bit位来表示。

     一共有8个定义，所以整个抽象为8位
     
     如果在BB中出现就对应标为1，如果被kill就对应标为0

   • 迭代

     • 第一次迭代（黑色）：初始化，将所有的OUT都设为0000 0000
       

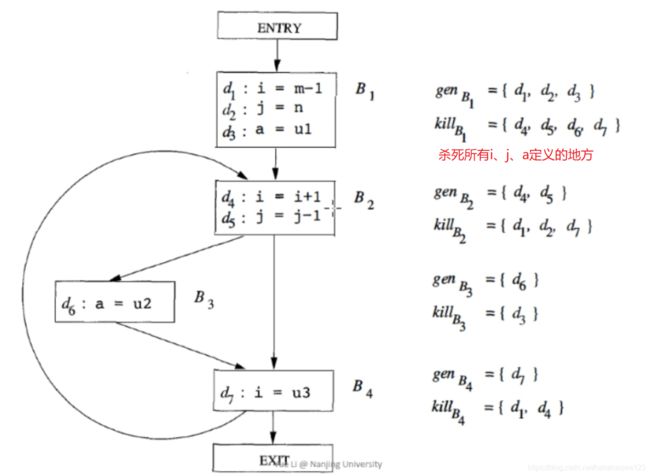
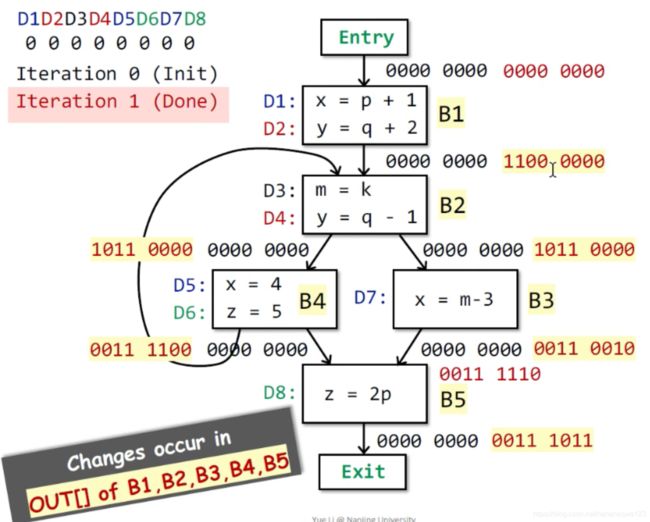
     • 第二次迭代（红色）：因为在第一次迭代中，所有的OUT均有变化，所以需要第二次迭代=>从上向下计算

       OUT[B1] = 1100 0000

       B2有两个输入：是OUT[B4]和OUT[B1]的并集=>1100 0000 v 0000 0000 = 1100 0000

       OUT[B2] = 1011 0000(从1100 0000 由于D2被kill，所以为0，D3、D4产生，所以为1)

       B2到B3、B4是分支的分叉，所以B4、B3的输入都为OUT[B2]

       OUT[B3] = 0011 0010

       OUT[B4] = 0011 1100

       B5是B3和B4的合并，所以是计算B3、B4的并集：0011 0010 v 0011 1100 = 0011 1110

       OUT[B5] = 0011 1011
       

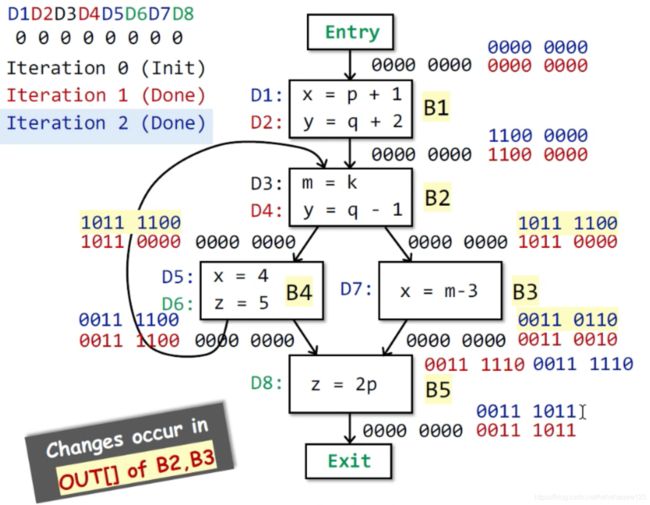
     • 第三次迭代（蓝色） => 由于第二次迭代中，所有OUT均产生变化，所以需要第三次迭代

       OUT[B1] = 1100 0000不发生变化

       B2的输入发生变化（因为B1的输出不发生变化，而B4的输出发生了变化）

       ​ => 0011 1100 v 1100 0000 = 11111100

       OUT[B2] = 1011 1100

       OUT[B3] = 0011 0110 由于B2的OUT变化了

       OUT[B4] = 0011 1100 由于B2的OUT变化了，但是结果和上一次一样

       B5的输入：0011 1100 V 0011 0110 = 0011 1110

       OUT[B5] = 0011 1011 结果和第一次迭代一样
       

     • 第四次迭代：由于B2、B3变化了，所以还需要迭代

       OUT[B1]是不会发生变化了；

       对于B2由于OUT[B1]和OUT[B4]未发生变化，所以不需要再计算，是不会变化的了

       对于B3、B4，由于OUT[B2]未发生变化，所以不需要计算，不变

       同理，对于B5，输入不变也不用变化

     => 我们可以发现：如果输入不变，则输出是不会发生变化的。

     根据$OUT[B]=ge{n}_B\cup (IN[B]-kil{l}_B)$，只要BB中的语句不发生变化，那么gen和kill都不会发生变化，则输出只跟输入有关。

     • 迭代结束：由于第四次迭代后所有的OUT都没有变化，所以算法结束

     =>看到，每个程序点都有一个数据流值（0001 1100），这个值就是对程序状态的一个抽象，具体到该可达定义中，就是我们能通过该数据流值看到某个定义是否能到达该程序点

     =>看到，整个算法就是不断应用安全近似的约束条件（控制流、转换函数），直到算法结束，我们能找到一个解关于所有的定义

   • 算法分析

     • 算法能否终止

       根据上面能发现：对于一个BB，gen和kill是对固定位进行操作的，即一旦经过计算，gen对应的位一定会成1，kill的位一定会成0，所以OUT的变化只跟IN有关系

       我们称：$IN[S]-kil{l}_s$后的为survivor（幸存者），一旦它幸存了，它就一直存在不会消失了（不存在这一次幸存，下一次被kill的）

       关键点：OUT[S]永远不会缩小

       所以OUT会不断变大，直到不变为止，最坏的情况都是全1，所以算法一定会停止
       

     • 为啥OUT不变了，就可以认为停止了（即为最终结果）：

       因为由于OUT都不变了，则对应BB块的下一个输入也不会变化，则OUT仍然不会变，达到了一个不动点。

     所以，该算法又称：不动点算法。

4.live变量的分析

1. 定义：是否存在一条路径，使得从程序点p开始沿着该路径，v被使用。如果是，v在p点就是live的，否则，v在p点就是dead的。

   隐含着：v在该路径上，在使用之前没有被重新定义。

   是may analysis：因为是考虑某些路径是否live
   

2. 实际应用：能够将live变量的信息用于寄存器分配，程序运行到某个点，发现所有寄存器都满了，但是我们需要替换出空间放新的值，所以可以将dead变量的寄存器空出来。

3. 具体理解

   • 抽象：方法和可达定义的方法类似，将每个变量出现的先后分别编号，然后分别用1bit来表示，从左向右依次增加
     

   • 安全近似

     采用backwards更直观，就是从use那一点回溯之前被定义的点：所以是给定OUT[B]去求IN[B]

     • 转换函数

       use[B]：在B中v在被重新定义前使用

       def[B]：在B中v被重新定义

       $IN[B]=us{e}_B\cup (OUT[B]-de{f}_B)$

       去掉已经被重新定义的，加上被使用的

       举例：
       

     • 控制流

       $OUT[B]={\bigcup }_{SasuccessorofB}IN[S]$

       就是待求的程序点B的OUT就是B的所有后继的IN的并集。

4. live变量算法实现
   
   初始化最后一个结点的in为空，并且初始化每个结点的in为空

   ps：may analysis初始化均为空，must analysis初始化均为all

   举例：

   ​ 有7个变量，所以有7个bit

   • 第一次迭代：初始化

     将所有的BBs的IN都赋值为 000 0000
     

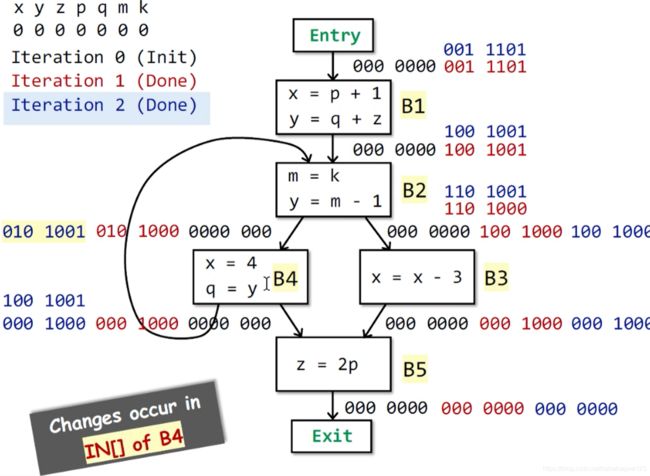
   • 第二次迭代：由于第一次迭代所有BB的IN发生了变化，所以还需要继续迭代

     OUT[B5] = 000 0000 ，IN[B5] = 000 1000（z被kill掉，p被use）

     OUT[B3] = IN[B5] = 000 1000 ，IN[B3] = 100 1000（x被kill掉。x被use）

     OUT[B4] = IN[B5] $\cup$ IN[B2] = 000 1000 $\cup$ 000 0000 = 000 1000 ，IN[B4] = 010 1000（x、q被kill掉，y被use）

     OUT[B2] = IN[B4] $\cup$ IN[B3] = 010 1000 $\cup$ 100 1000 = 110 1000 ，IN[B2] = 100 1001（m、y被kill掉，k被use）

     OUT[B1] = IN[B2] = 100 1001 ，IN[B1] = 001 1101（x、y被kill掉，p、q、z被use）
     

   • 第三次迭代：由于第二次迭代中，B1、B2、B3、B4、B5的IN都发生变化，所以需要继续迭代

     OUT[B5]没有发生变化，所以IN[B5]没变

     OUT[B3]=IN[B5]没变，所以IN[B3]没变

     OUT[B4] = IN[B5] $\cup$ IN[B2] = 000 1000 $\cup$ 100 1001 = 100 1001 发生变化，所以IN[B4] = 010 1001

     OUT[B2] = IN[B4] $\cup$ IN[B3] = 010 1001 $\cup$ 100 1000 = 110 1001发生变化，所以IN[B2] = 100 1001

     OUT[B1] = IN[B2]没有发生变化，所以IN[B1]没变
     

   • 第四次迭代：由于第三次迭代中，B4的IN发生变化（B2的OUT变了，但是算出的IN没变），所以需要继续迭代

     B5没变，B3没变

     由于OUT[B4] = IN[B5] $\cup$ IN[B2]，而B5、B2均没有变化，所以OUT[B4]没变，IN[B4]没变

     B2、B1没变

     所以该次迭代中，IN均没有变化，所以循环结束。第四次的结果就是最后的结果
     
     ps：应该是先计算def，再计算use

5.available表达式的分析

1. 定义：must analysis

   表达式 x op y在程序点p是available，要求：从入口到p点的所有路径都要去执行x op y操作，并且最后一次执行x op y后，x和y都不会被重新定义（？？？给的定义是这样的，不大能理解）

   其实就是，看表达式中是否有变量被重新赋值，如果重新赋值了，该表达式就不再available；一条语句执行一次表达式，该表达式就是available

2. 应用

   我们可以将最后执行的结果赋值给之后的x op y操作，以简化操作

3. 理解

   • 抽象

     将每个表达式都用1个bit来表示：1表示available，按照出现前后进行编号：
     

   • 安全近似（即使该表达式是真的available，但是结果是unavailable；它仍旧满足safe近似）

     举个例子：下图中，假设输入时候a+b是available，之后x op y是available，但是由于a被重新赋值，所以a+b不再available
     

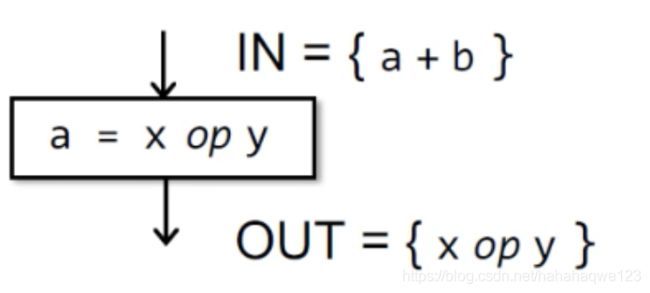
     • 转换函数

       $ge{n}_B$代表在BB中，新执行的表达式，就是available；$kil{l}_B$在BB中，表达式有任何一个变量被重新赋值了，则该表达式就被kill了

       这个和变量的可达定义类似
       
       举个复杂的例子：

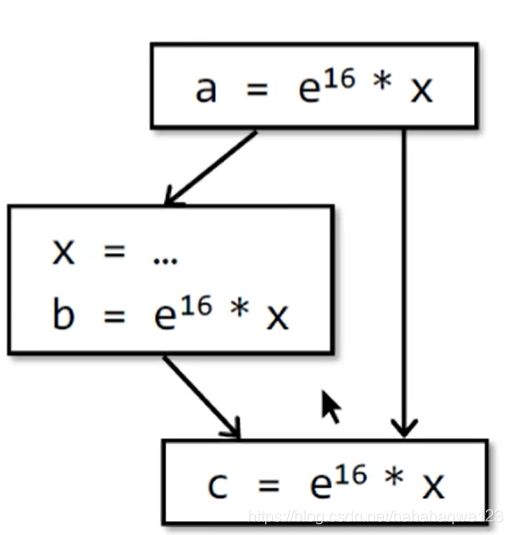
       假设我们只关注$e^{16}\ast x$这个表达式，执行完第一个BB得出该表达式available，执行左边的BB，首先x被重新赋值，所以表达式not available，然后之后又执行$e^{16}\ast x$，该表达式又available，所以两者结合，最下面的BB的输入中，$e^{16}\ast x$表达式是available。
       
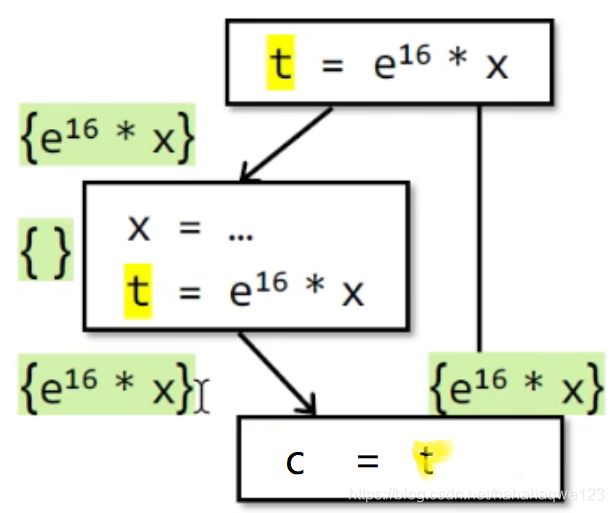
       那么可对它做如下优化：
       

     • 控制流
       
       它是所有B的前驱的OUT的交集

4. 算法实现

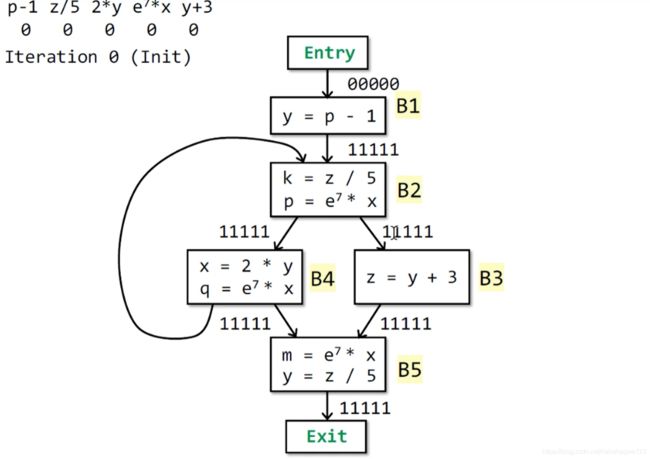
   初始化：入口为空；对于每个BB的OUT都初始化为11111（全为真）（可以直观的想到，由于BB的IN是其所有前驱OUT的并集，如果一开始有一个是0000，则全0和其他任何值相交都为空，所以之前的步骤都全部白做了，具体可以看下面举的例子）
   

5. 举例

   • 第一次迭代：初始化

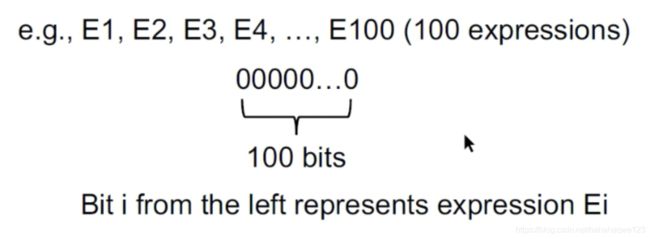
     该例子中有5个表达式，依次对其编号，然后OUT[entry] = 0 0000

     其余所有OUT = 0 0000
     

   • 第二次迭代：由于第一次迭代中，所有的OUT全部变化了，所以需要第二次迭代

     IN[B1] = OUT[entry] = 0 0000，OUT[B1] = 1 0000

     IN[B2] = OUT[B1] $\cap$ OUT[B4] = 1 0000 $\cap$ 1 1111 = 1 0000，OUT[B2] = 0 1010

     IN[B4] = OUT[B2] = 0 1010，OUT[B4] = 0 1110

     IN[B3] = OUT[B2] = 0 1010，OUT[B3] = 0 0011

     IN[B5] = OUT[B4] $\cap$ OUT[B3] = 0 1110 $\cap$ 0 0011 = 0 0010，OUT[B5] = 0 1010
     

   • 第三次迭代：由于第二低次迭代中，所有OUT均发生变化，所以需要继续迭代

     IN[B1] = 0 0000，由于输入没变，所以OUT[B1]没有变化，OUT[B1] = 1 0000

     IN[B2] = OUT[B1] $\cap$ OUT[B4] = 1 0000 $\cap$ 0 1110 = 0 0000，OUT[B2] = 0 1010

     IN[B4] = OUT[B2] = 0 1010，输入没变，所以OUT[B4]没变，OUT[B4] = 0 1110

     IN[B3] = OUT[B2] = 0 1010，输入没变。所以OUT[B3]没变，OUT[B3] = 0 0011

     IN[B5] = OUT[B4] $\cap$ OUT[B3] = 0 1110 $\cap$ 0 0011 = 0 0010，输入没变，所以OUT[B5]没变，OUT[B5] = 0 1010

     所以，本次迭代，所有OUT均没有发生变化，所以程序结束
     
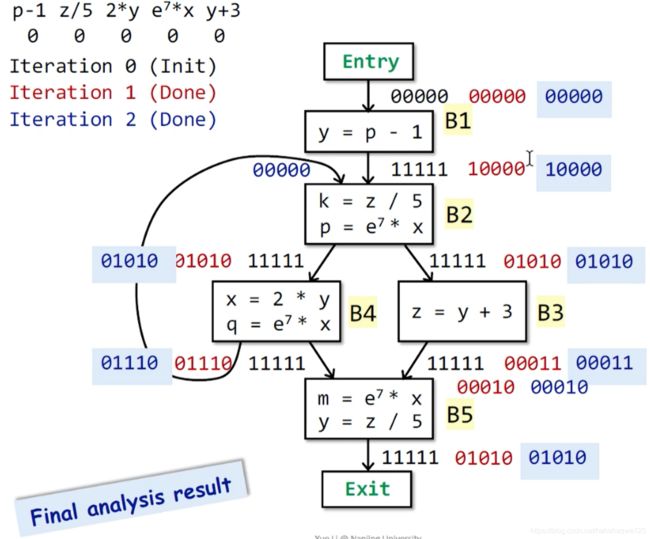
     最后一次迭代的结果，就是available的解
     ps：先做kill，再做gen

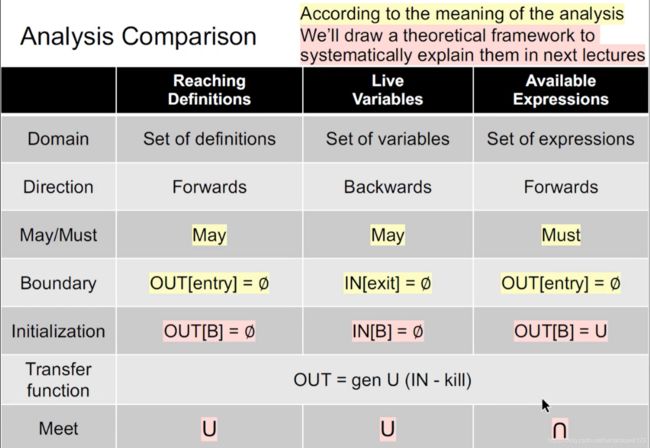
6. 三种分析的比较

解释：

1. 值域：分析啥看啥
   • 可达定义：一系列定义的集合，就是抽象中，每个定义给1bit来表示是否可达
   • live变量：一系列变量的集合，抽象中，每个变量给1bit来表示是否live
   • available表达式：一系列表达式的集合，抽象中，每个表达式给1bit来表示是否有效
2. 方向：就是分析中，是前向还是反向分析
3. 界限：就是初始化中，是初始化entry还是exit，这个和前向/反向分析
4. 初始化：关于所有BB的初始化时，初始化IN还是OUT，初始化全真/全假
5. meet操作：有多个输出/输入的时候，到下个BB时，该进行的操作

以上就是这两节的全部内容，这周我应该会再学习2节，最近欠了各个老师好多的课和任务，希望周日能将最新的更新上来！（给自己立个flag）