一文读懂sum-product算法
变量划分
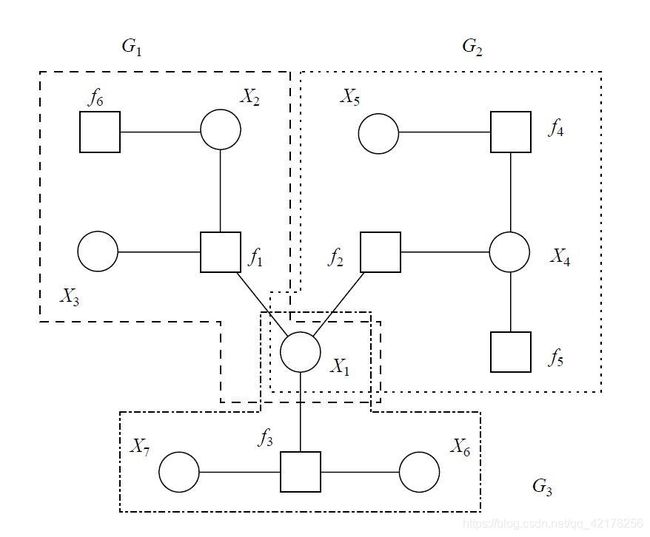如上图，一个树状的因子图（无环且连接），去掉图中一个变量节点（例如图中的 X 1 X_1 X1），因子图被分解为三部分。
定义集合 S f 1 ( X 1 ) = { X 2 , X 3 } S_{f_1}^{(X_1)}=\{X_2,X_3\} Sf1(X1)={ X2,X3}， S f 2 ( X 1 ) = { X 4 , X 5 } S_{f_2}^{(X_1)}=\{X_4,X_5\} Sf2(X1)={ X4,X5}. S f 3 ( X 1 ) = { X 6 , X 7 } S_{f_3}^{(X_1)}=\{X_6,X_7\} Sf3(X1)={ X6,X7}。明确一点 S f 1 ( X 1 ) ∪ S f 2 ( X 1 ) ∪ S f 3 ( X 1 ) ∪ { X 1 } = { X 1 , X 2 , . . . , X 7 } S_{f_1}^{(X_1)}\cup S_{f_2}^{(X_1)} \cup S_{f_3}^{(X_1)} \cup \{X_1\}=\{X_1,X_2,...,X_7\} Sf1(X1)∪Sf2(X1)∪Sf3(X1)∪{ X1}={ X1,X2,...,X7}，并且 S f k ( X 1 ) ∩ S f j ( X 1 ) = ϕ S_{f_k}^{(X_1)}\cap S_{f_j}^{(X_1)}=\phi Sfk(X1)∩Sfj(X1)=ϕ。
显然有
f ( X 1 , X 2 , . . . , X 7 ) = ∏ f k ∈ N ( X 1 ) h f k ( X 1 ) ( X 1 , S f k ( X 1 ) ) f(X_1,X_2,...,X_7)=\prod\limits_{f_k \in N(X_1)}{h_{f_k}^{(X_1)}(X_1,S_{f_k}^{(X_1)})} f(X1,X2,...,X7)=fk∈N(X1)∏hfk(X1)(X1,Sfk(X1))
对于任何一个变量节点都可以做这种分解，这里只拿 X 1 X_1 X1举一个例子。任选一个变量节点 X n X_n Xn
f ( X 1 , X 2 , . . . , X N ) = ∏ f k ∈ N ( X n ) h f k ( X n ) ( X n , S f k ( X n ) ) f(X_1,X_2,...,X_N)=\prod\limits_{f_k \in N(X_n)}{h_{f_k}^{(X_n)}(X_n,S_{f_k}^{(X_n)})} f(X1,X2,...,XN)=fk∈N(Xn)∏hfk(Xn)(Xn,Sfk(Xn))
我们能否递归地求解 h f k ( X n ) ( X n , S f k ( X n ) ) {h_{f_k}^{(X_n)}(X_n,S_{f_k}^{(X_n)})} hfk(Xn)(Xn,Sfk(Xn))？
一次划分之后，每一个部分都跟在一个 f k f_k fk之后，写下因子 f k ( { X m } ∈ N ( f k ) ) f_k(\{X_m\}\in N(f_k)) fk({ Xm}∈N(fk))，拿掉 f k f_k fk相当于把这一部分进一步划分为 N ( f k ) − 1 N(f_k)-1 N(fk)−1部分(出去 X n X_n Xn)。
h f k ( X n ) ( X n , S f k ( X n ) ) = f k ( { X m } ∈ N ( f k ) ) ∏ X m ∈ N ( f k ) / X n { ∏ f l ∈ N ( X m ) / f k h f l ( X m ) ( X m , S f l ( X m ) ) } {h_{f_k}^{(X_n)}(X_n,S_{f_k}^{(X_n)})}=f_k(\{X_m\}\in N(f_k))\prod\limits_{X_m\in N(f_k)/X_n}{\{\prod\limits_{f_l\in N(X_m)/f_k}{ {h_{f_l}^{(X_m)}(X_m,S_{f_l}^{(X_m)})}}\}} hfk(Xn)(Xn,Sfk(Xn))=fk({ Xm}∈N(fk))Xm∈N(fk)/Xn∏{ fl∈N(Xm)/fk∏hfl(Xm)(Xm,Sfl(Xm))}
划分到边缘( N ( f k ) / X n N(f_k)/X_n N(fk)/Xn或 N ( X m ) / f k N(X_m)/f_k N(Xm)/fk为空集)停止，也就是说再往后没有其他因子了，连乘项变为1。这里可以想一下上图中 h f 1 X 1 h_{f_1}^{X_1} hf1X1和 h f 6 X 2 h_{f_6}^{X_2} hf6X2的计算。
边缘计算
计算 x n x_n xn的边缘分布
g ( x n ) = ∑ ∼ { x n } ∏ f k ∈ N ( x n ) h f k ( x n ) ( x n , S f k ( x n ) ) g(x_n)=\sum\limits_{\sim \{x_n\}}{\prod\limits_{f_k\in N(x_n)}}{h_{f_k}^{(x_n)}(x_n,S_{f_k}^{(x_n)})} g(xn)=∼{ xn}∑fk∈N(xn)∏hfk(xn)(xn,Sfk(xn))
注意根据划分 S f k x n S_{f_k}^{x_n} Sfkxn是互不相交的。那么
g ( x n ) = ∏ f k ∈ N ( x n ) ∑ S f k ( x n ) h f k ( x n ) ( x n , S f k ( x n ) ) g(x_n)={\prod\limits_{f_k\in N(x_n)}}\sum\limits_{S_{f_k}^{(x_n)}}{h_{f_k}^{(x_n)}(x_n,S_{f_k}^{(x_n)})} g(xn)=fk∈N(xn)∏Sfk(xn)∑hfk(xn)(xn,Sfk(xn))
定义两个关于 x n x_n xn的函数
消息1
μ f k → x n ( x n ) = ∑ S f k ( x n ) h f k ( x n ) ( x n , S f k ( x n ) ) = ∑ ∼ { x n } h f k ( x n ) ( x n , S f k ( x n ) ) \mu_{f_k\to x_n}(x_n)=\sum\limits_{S_{f_k}^{(x_n)}}{h_{f_k}^{(x_n)}(x_n,S_{f_k}^{(x_n)})} =\sum\limits_{\sim \{x_n\}}{h_{f_k}^{(x_n)}(x_n,S_{f_k}^{(x_n)})} μfk→xn(xn)=Sfk(xn)∑hfk(xn)(xn,Sfk(xn))=∼{ xn}∑hfk(xn)(xn,Sfk(xn))
μ f k → x n ( x n ) = ∑ ∼ { x n } f k ( { X m } ∈ N ( f k ) ) ∏ X m ∈ N ( f k ) / X n { ∏ f l ∈ N ( X m ) / f k h f l ( X m ) ( X m , S f l ( X m ) ) } \mu_{f_k\to x_n}(x_n)=\sum\limits_{\sim\{x_n\}}{f_k(\{X_m\}\in N(f_k))\prod\limits_{X_m\in N(f_k)/X_n}{\{\prod\limits_{f_l\in N(X_m)/f_k}{ {h_{f_l}^{(X_m)}(X_m,S_{f_l}^{(X_m)})}}\}}} μfk→xn(xn)=∼{ xn}∑fk({ Xm}∈N(fk))Xm∈N(fk)/Xn∏{ fl∈N(Xm)/fk∏hfl(Xm)(Xm,Sfl(Xm))}
μ f k → x n ( x n ) = ∑ ∼ { x n } f k ( { X m } ∈ N ( f k ) ) ∏ X m ∈ N ( f k ) / X n μ x n → f l ( x n ) \mu_{f_k\to x_n}(x_n)=\sum\limits_{\sim\{x_n\}}{f_k(\{X_m\}\in N(f_k))\prod\limits_{X_m\in N(f_k)/X_n}{\mu_{x_n\to f_l}(x_n)}} μfk→xn(xn)=∼{ xn}∑fk({ Xm}∈N(fk))Xm∈N(fk)/Xn∏μxn→fl(xn)
消息2
μ x n → f k ( x n ) = ∏ f l ∈ N ( x n ) / f k ∑ S f l ( x n ) h f l ( x n ) ( x n , S f l ( x n ) ) \mu_{x_n\to f_k}(x_n)={\prod\limits_{f_l\in N(x_n)/f_k}}\sum\limits_{S_{f_l}^{(x_n)}}{h_{f_l}^{(x_n)}(x_n,S_{f_l}^{(x_n)})} μxn→fk(xn)=fl∈N(xn)/fk∏Sfl(xn)∑hfl(xn)(xn,Sfl(xn))
μ x n → f k ( x n ) = ∏ f l ∈ N ( x n ) / f k μ f l → x n ( x n ) \mu_{x_n\to f_k}(x_n)={\prod\limits_{f_l\in N(x_n)/f_k}}\mu_{f_l\to x_n(x_n)} μxn→fk(xn)=fl∈N(xn)/fk∏μfl→xn(xn)
因而 g ( x n ) g(x_n) g(xn)可以表示为
g ( x n ) = ∏ f k ∈ N ( x n ) μ f k → x n ( x n ) g(x_n)=\prod\limits_{f_k\in N(x_n)}\mu_{f_k \to x_n}(x_n) g(xn)=fk∈N(xn)∏μfk→xn(xn)
g ( x n ) = μ f l → x n ( x n ) μ x n → f l ( x n ) f o r a n y f l g(x_n)=\mu_{f_l \to x_n}(x_n)\mu_{x_n \to f_l}(x_n) \quad for \, any \, f_l g(xn)=μfl→xn(xn)μxn→fl(xn)foranyfl
如果我们能求出所有的 μ x n → f l , μ f l → x n \mu_{x_n \to f_l}, \mu_{f_l \to x_n} μxn→fl,μfl→xn，那么所有的边缘分布就可以得到。
观察消息1和消息2的本质，当因子节点 f k f_k fk为一个叶节点， N ( f k ) / X n = ϕ N(f_k)/X_n=\phi N(fk)/Xn=ϕ,后面的连乘项为1，此时
μ f k → x n = f k ( x n ) \mu_{f_k\to x_n}=f_k(x_n) μfk→xn=fk(xn)
当变量节点为叶节点， N ( X m ) / f k = ϕ N(X_m)/f_k=\phi N(Xm)/fk=ϕ
μ x n → f k = 1 \mu_{x_n\to f_k}=1 μxn→fk=1
算法过程
初始：
从叶节点开始直接得到 μ x n → f l , μ f l → x n \mu_{x_n \to f_l}, \mu_{f_l \to x_n} μxn→fl,μfl→xn
中间计算：
一个节点的度为D（根据上面式子，一个节点要收到（已知）D-1个消息后去算最后一个边出去的消息），一轮消息计算完之后挑选那些D-1个消息已知的节点去算。
结束：
有的消息计算完。
注意：因子图中有环的话，上述算法的第二部就不能实现了，环中的节点互相需要对方的消息才能继续计算，无法开始。