位运算笔记
本文大部分学习自一篇名为《位运算讲稿 by matrix 67》的pdf,并随性记录成个人笔记。
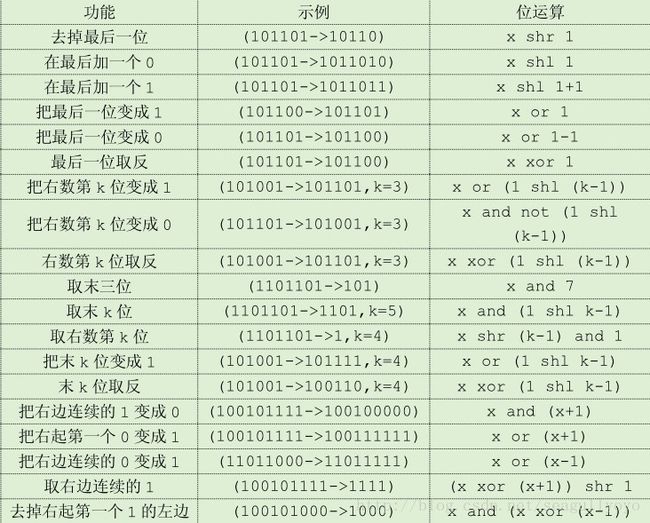
各种位运算的使用
=== 1. and 运算 ===
and 运算通常用于二进制取位操作,例如一个数 and 1 的结果就是取二进制的最末位。这可以用来判断一个整数的奇偶,二进制的最末位为 0 表示该数为偶数,最末位为 1 表示该数为奇数.
=== 2. or 运算 ===
or 运算通常用于二进制特定位上的无条件赋值,例如一个数 or 1 的结果就是把二进制最末位强行变成 1。如果需要把二进制最末位变成 0,对这个数 or 1 之后再减一就可以了,其实际意义就是把这个数强行变成最接近的偶数。
=== 3. xor 运算 ===
xor 运算通常用于对二进制的特定一位进行取反操作,因为异或可以这样定义:0 和 1 异或 0 都不变,异或 1则取反。xor 运算的逆运算是它本身,也就是说两次异或同一个数最后结果不变,即(a xor b) xor b = a。xor运算可以用于简单的加密,比如我想对我 MM说 1314520,但怕别人知道,于是双方约定拿我的生日 19880516作为密钥。1314520 xor 19880516 = 20665500,我就把 20665500 告诉 MM。MM 再次计算 20665500 xor 19880516 的值,得到 1314520,于是她就明白了我的企图。
=== 4. not 运算 ===
not 运算的定义是把内存中的 0 和 1 全部取反。使用 not 运算时要格外小心,你需要注意整数类型有没有符号。如果 not 的对象是无符号整数(不能表示负数) ,那么得到的值就是它与该类型上界的差;如果not的对象是有符号整数,not后会得到得到一个正数。
=== 5. shl 运算 ===
a shl b就表示把a转为二进制后左移b位 (在后面添b个0) 。 例如100的二进制为1100100, 而110010000转成十进制是 400,那么 100 shl 2 = 400。可以看出,a shl b 的值实际上就是 a 乘以 2 的 b 次方,因为在二进制数后添一个 0 就相当于该数乘以 2。
通常认为 a shl 1 比 a * 2 更快,因为前者是更底层一些的操作。因此程序中乘以 2 的操作请尽量用左移一位来代替。定义一些常量可能会用到 shl 运算。你可以方便地用 1 shl 16 - 1 来表示 65535。很多算法和数据结构要求数据规模必须是 2 的幂,此时可以用 shl 来定义 Max_N 等常量。
=== 6. shr 运算 ===
和 shl 相似,a shr b 表示二进制右移 b 位(去掉末 b 位) ,相当于 a 除以 2 的 b 次方(取整) 。我们也经常用 shr 1 来代替 div 2,比如二分查找、堆的插入操作等等。想办法用 shr 代替除法运算可以使程序效率大大提高。最大公约数的二进制算法用除以 2 操作来代替慢得出奇的 mod 运算,效率可以提高 60%。
留意一下最后几个,还挺有意思的。没看这文章的话,我估计就会去倒腾循环了。
整数类型的储存
#include
int main()
{
short int a, b;
a = 0x0000;
b = 0x0001;
printf( "%d %d ", a, b );
a = 0xFFFE;
b = 0xFFFF;
printf( "%d %d ", a, b );
a = 0x7FFF;
b = 0x8000;
printf( "%d %d\n", a, b );
return 0;
} tricks
只用位运算来取绝对值
int t = -7//7;
cout << (t >> 31) << endl;
int abst = ( ( ~((t >> 31) & 1 ) + 1 ) ^ t) + ((t >> 31) & 1);
cout << "t: " << t << " abs(t): " << abst << endl;
1)绝对值,对正数来说就是不变,负数要取反+1(补码计算);
2)负数+1、正数+0这一步简单,+他们的符号位就好了 + ((t >> 31) & 1);
3)下边处理负数取反正数不变这一块。而想到取反,显然要跟异或挂钩,即异或全1(0xFFFFFFFF);正数我们不想变,异或全0(0x00000000 )就好了。而 ~1 + 1 是全1, ~0 + 1 是全0(因为溢出)。
合起来,就是 t ^ (~((t >> 31) & 1) + 1) + ((t >> 31) & 1) 。
交换高低位
给出一个小于 2^32 的正整数。这个数可以用一个 32 位的二进制数表示(不足 32 位用 0 补足) 。我们称这个二进制数的前 16 位为“高位”,后 16 位为“低位”。将它的高低位交换,我们可以得到一个新的数。试问这个新的数是多少(用十进制表示) 。
int p = 0xabcd1234;
printf("p : 0x%x\n", p);
int q = (p & 0xffff0000) >> 16 | (p & 0x0000ffff) << 16;
printf("q : 0x%x\n", q);
二进制逆序
下面的程序读入一个 32 位整数并输出它的二进制倒序后所表示的数。输入: 1314520 (二进制为 00000000000101000000111011011000)
输出: 460335104 (二进制为 00011011011100000010100000000000)
心路历程:
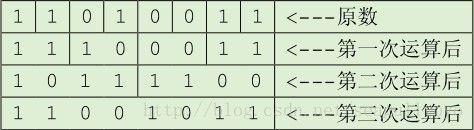
当然可以用栈来实现,但是用位运算实现显然逼格更高。首先交换每相邻两位上的数,以后把互相交换过的数看成一个整体,继续进行以 2 位为单位、以4 位为单位的左右对换操作。用8 位整数211来演示程序执行过程:
代码如下:
int main(void)
{
int a = 0xb953ced5;
printf("0x%x\n", a);
a = ( ((a & 0xaaaaaaaa) >> 1) | ((a & 0x55555555) << 1) );
a = ( ((a & 0xcccccccc) >> 2) | ((a & 0x33333333) << 2) );
a = ( ((a & 0xf0f0f0f0) >> 4) | ((a & 0x0f0f0f0f) << 4) );
a = ( ((a & 0xff00ff00) >> 8) | ((a & 0x00ff00ff) << 8) );
a = ( ((a & 0xffff0000) >> 16) | ((a & 0x0000ffff) << 16) );
printf("0x%x\n", a);
return 0;
}应用
2.5 亿个数的去重
在 2.5 亿个整数中找出不重复的整数,注,内存不足以容纳这 2.5 亿个整数分析:采用 2-Bitmap(每个数分配 2bit,00 表示不存在,01 表示出现一次,10 表示多次,11 无意义)
进行,共需内存 2^32 * 2 bit=1 GB 内存,还可以接受。然后扫描这 2.5 亿个整数,查看 Bitmap 中相对应位,
如果是 00 变 01,01 变 10,10 保持不变。所描完事后,查看 bitmap,把对应位是 01 的整数输出即可。
给 40 亿个不重复的 unsigned int 的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那 40 亿个数当中?
unsigned int 最大为 2^33 - 1,也就是8589934591,80亿量级。100亿个bit足够,也就是12.5亿个byte,125W个Kb,125M,也即申请125M 连续的内存,对这40亿个数对应的偏移bit位置1,然后看新输入的数查看对应位置为0或1即可。