OpenCV Using Python——构造方向可控金字塔

构造方向可控金字塔

1. 方向可控金字塔简介

       Willian T. Freeman等1991年提出方向可控金字塔。和高斯金字塔或拉普拉斯金字塔相比，方向金字塔除了分解尺度子带以外，还会分解方向子带。为什么需要用方向子带呢？因为在图像匹配等应用场合中，尺度变化外加旋转操作计算量很大。微分计算获得方向和多尺度的金字塔同时具有线性和平移不变性，所以考虑将尺度和方向结合起来操作。

2. 拉普拉斯金字塔，双尺度小波变换和方向可控金字塔比较

（1）紧框架

        紧框架是指变换矩阵的逆矩阵等于变换矩阵的转置。在构造图像金字塔时需用不同的带通滤波器对图像作分解，而这些带通滤波器以矩阵的形式出现，而在图像重构需用不同的带通滤波器的逆矩阵对图像重建。因为矩阵求逆比较耗时，所以紧框架的性质会大大加快图像重建的计算速度。拉普拉斯金字塔不具有紧框架性质；双尺度小波变换和尺度金字塔具有紧框架性质。

（2）过完备

        拉普拉斯金字塔过完备性为4/3，双尺度小波变换过完备性为1，方向可控金字塔过完备性为4k/3。过完备是指信息的冗余量。方向金字塔包含方向信息时，描述同一幅图像占用的资源最多。

（3）混叠

        拉普拉斯金字塔有可能发生混叠；双尺度小波变换一定会混叠；尺度金字塔不会混叠。

（4）旋转方向子带

        拉普拉斯金字塔没有方向子带；小波变换在六角晶格上有方向子带；方向可控金字塔有方向子带。

        综上， 方向可控金字塔是占用资源和方向个数成正比的，重建速度快，不会混叠的，同时有尺度和方向子带的图像表示。（P.S. 双尺度小波变换还没用过，支线加上不懂先跳过）

3. 构造方向可控金字塔滤波器

        用方向可控金字塔分解图像最重要的是构造方向子带的滤波器。不过，OpenCV没有给我们提供这样的库函数，所以只能自己写构造过程了。幸运的是，K. R. Castleman等的文章“方向可控滤波器的简单设计”给我们提供了滤波器的构造方法。根据它笔者实现了方向可控金字塔滤波器的构造。

（1）实现代码

import cv2
import csv
import math
import numpy as np
from matplotlib import cm
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
################################################################################

print 'parameter set'

f1 = 0
f2 = math.pi * 5 / 8
fn = math.pi
################################################################################

print 'range of u and v'

umin, umax, du = -fn, fn, 0.25
vmin, vmax, dv = -fn, fn, 0.25

ulist = np.arange(umin, umax, du)
vlist = np.arange(vmin, vmax, dv)

'''
ulist = []
vlist = []
for i in range(int((umax - umin) / du)):
    ulist.append(umin + du * i)
for j in range(int((vmax - vmin) / dv)):    
    vlist.append(vmin + dv * j)
'''    
################################################################################

# lowpass filter function

def lowpass(f, a, b):
    
    if f < a or f == a:
        s = 1
    elif f > a and f < b:
        s = math.sqrt(0.5 * (1 + math.cos(math.pi * (f - a) / (b - a)))) 
    else:
        s = 0        
    return s

# highpass filter function

def highpass(f, a, b):
    
    if f < a or f == a:
        s = 0
    elif f > a and f < b:
        s = math.sqrt(0.5 * (1 - math.cos(math.pi * (f - a) / (b - a)))) 
    else:
        s = 1       
    return s

# build lowpass or highpass filter

def passFilter(ulist, vlist, a, b, case):

    P = []
    for u in ulist:       
        U = []
        
        for v in vlist:            
            f = math.sqrt(u * u + v * v)
            if case.lower() == 'l':      
                s = lowpass(f, a, b)
            elif case.lower() == 'h':
                s = highpass(f, a, b)               
            U.append(s)       
        P.append(U)
            
    return P
################################################################################

print 'Lowpass Filter L0(u,v)'

LP0 = passFilter(ulist, vlist, f2, math.pi, 'l')

print 'Lowpass Filter L1(u,v)'

LP1 = passFilter(ulist, vlist, f1, fn / 2, 'l')

LP = []
LP.append(LP0)
LP.append(LP1)
################################################################################

print 'Highpass Filter H0(u,v)'

HP0 = passFilter(ulist, vlist, f2, fn, 'h')

print 'Highpass Filter H1(u,v)'

HP1 = passFilter(ulist, vlist, f1, fn / 2, 'h')

HP = []
HP.append(HP0)
HP.append(HP1)
################################################################################         

print 'Steerable Bandpass Filter'

# k = 2, sm(m = 0,...,k - 1)

def steerableBandpass(ulist, vlist, HP):
    
    B0 = []
    B1 = []
    
    for u in range(len(ulist)):
        U0 = []
        U1 = []
        
        for v in range(len(vlist)):
            s0 = HP[u][v] * math.cos(math.atan2(ulist[v], ulist[u]))
            s1 = HP[u][v] * math.cos(math.atan2(ulist[v], ulist[u]) + math.pi / 2)
            U0.append(s0)
            U1.append(s1)
            
        B0.append(U0)
        B1.append(U1)
    
    return B0, B1

B0, B1 = steerableBandpass(ulist, vlist, HP1)
################################################################################

print 'display filters'

fig = plt.figure()

ax = fig.add_subplot(231, projection = '3d')
U, V = np.meshgrid(ulist, vlist) 
surf = ax.plot_surface(U, V, LP0, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=False) 

ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('L0')
                  
ax = fig.add_subplot(232, projection = '3d')
U, V = np.meshgrid(ulist, vlist) 
surf = ax.plot_surface(U, V, LP1, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=False)

ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('L1')

ax = fig.add_subplot(233, projection = '3d')
U, V = np.meshgrid(ulist, vlist) 
surf = ax.plot_surface(U, V,HP0, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=False) 

ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('H0')
                  
ax = fig.add_subplot(234, projection = '3d')
U, V = np.meshgrid(ulist, vlist) 
surf = ax.plot_surface(U, V, HP1, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=False)

ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('H1')

ax = fig.add_subplot(235, projection = '3d')
U, V = np.meshgrid(ulist, vlist) 
surf = ax.plot_surface(U, V, B0, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=False) 

ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('B1')        
                        
ax = fig.add_subplot(236, projection = '3d')
U, V = np.meshgrid(ulist, vlist) 
surf = ax.plot_surface(U, V, B1, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=False)

ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('B2')

plt.show() 
################################################################################

print 'Goodbye!'

（2）实验结果

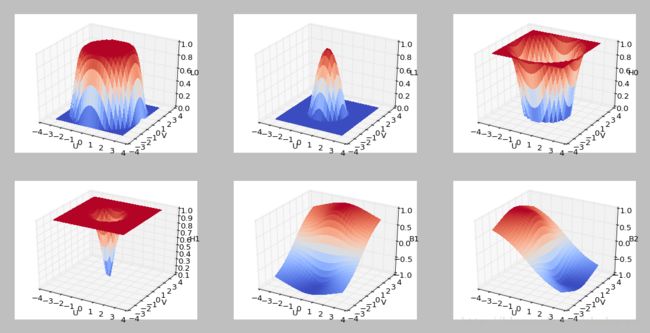
        和文章中的结果一样，这里给出笔者的滤波器（k=2时，即包含水平和垂直方向）绘制结果。上左图为低通滤波器L0（u,v），上中图为低通滤波器L1（u,v）,上右图为高通滤波器H0（u,v）,下左图为高通滤波器H1（u,v）,下中和下右图分别为带通滤波器B0(u,v)和B1（u,v）。u,v为频率域中的频率变量，范围为[-pi,pi]。

4. 使用方向可控金字塔滤波器

        笔者这里用一用方向可控金字塔滤波器中的方向子带滤波器实现，使用这个滤波器比较麻烦，这里涉及到离散傅里叶变换。离散傅里叶变换将空间域中的图像转换到频域中，频域图的中心为直流信号，横轴为频率u，纵轴为频率v。频率越高，边缘信息越多。方向子带滤波器滤除了频谱值低于f1和频谱值高于fn的信号，同时有不同的方向。所以，方向滤波器滤波后的图像边缘也会带有方向性。笔者用上面的滤波器B0（u,v）和B1(u,v)来得到带方向信息的边缘。

（1）傅里叶变换

        大多数频域中计算的图像都是正方形的，笔者认为有某些潜在的方便（试过长方形的图片也可以）。不过还是拿传统的情况来说明问题吧。首先加载灰度图像，然后以矩形图像中心为正方形中心剪裁图像至正方形。对正方形图像作傅里叶变换得到图像的频域。下面给出傅里叶变换代码。

################################################################################

print 'Fourier Transform'

# convert image to frequency domain
f = np.fft.fft2(imgGray)
# shift the center
fShift = np.fft.fftshift(f)

（2）频率域滤波

        图像滤波在空间域中为图像和图像模板的卷积，而空间域中两个函数卷积的傅里叶变换等于两个函数傅里叶变换在频域中的乘积。所以转换到频域中滤波就方便多了。Python中的变量都为引用，所以，如果函数返回值为输入变量，则可以不用返回任何值。P为方向子带滤波器，length为图片长度，pShift为图像的频率（复数）。

################################################################################

# get frequency domain using bandpass filter

def freqDomain(length, P, pShift):

    for u in range(length):
        for v in range(length):    
            # warning: elements in pShift must be complex number!
            # no cast from complex to float using '=' operator  
            pShift[u][v] = fShift[u][v] * P[u][v]
    
    return

（3）傅里叶逆变换

      频率域滤波完成后转换回空间域得到空间域中的图像。

################################################################################

# inverse fourier transform

def invFft(pShift):                                                                                    
    # shift the center back
    pIShift = np.fft.ifftshift(pShift)
    
    # inverse fft
    imgIf = np.fft.ifft2(pIShift)
    imgIf = np.abs(imgIf)
    
    return imgIf

（4）实验结果

        采用方向子带滤波器B0（u,v）和B1（u,v）得到滤波后的图像。Bandpass Filter 0和1分别为B0（u,v）和B1（u,v），FFT为未滤波的傅里叶变换的频谱，Filtered FFT为使用滤波器后的频谱，Inverse FFT逆变换得到滤波后的图像。从B0（u,v）可以看出滤波器的梯度方向为从下往上，滤波后的图像显示出从下往上变化巨大的水平边缘；同理，从B0（u,v）可以看出滤波器的梯度方向为从右往左，滤波后的图像显示出从右往左变化巨大的垂直边缘。

5. 构造方向可控金字塔实现

      与K. R. Castleman的文章的成果一致，笔者这里也构造起两层金字塔。构造两层金字塔需要在上面的基础上对图像再进行一次下采样，可以参考前一篇文章来调用pyDown()函数。与上一篇构造金字塔的文章一样，显示的图片大小相同，但像素大小不同。A*对应的图像为用A（u,v）滤波器滤波后的结果。

结语

        后来Paul Viola和Michael J. Jones的人脸检测中用矩形框特征代替了方向可控金字塔，文章中提到方向可控金字塔的计算比较复杂。滤波器的设计部分确实比较复杂，因为需要同时满足紧框架的若干个方程，但Viola在提取特征部分只是替换了滤波器的设计过程，可见带方向的金字塔的思想的重要性。另外，不同的图像会有不同的滤波器，因为不同图像的边缘信息有可能在频率域中的频率不同，所以，针对不同的应用需要调整带通参数f1,f2,fn来得到比较理想的不同方向的边缘。