高斯过程和机器学习1——高斯回归
introduction
监督学习一般有两种处理,一种是根据经验特点严格限制为莫一种模型和函数,比如用线性回归模型处理;另外一种就是更宽泛:给每一种函数模型一个先验概率,概率越大意味着越容易被我们采纳,意味它具有某种更好的性质,比如更为光滑(可以参考核密度估计的由来)。后者麻烦在函数模型是个无限集,如何处理?我们便推出一种【高斯过程】:是高斯分布的广义泛化。【随机过程】宽泛的解释是把函数值视为一个长的向量的多维(理论上无限维,观察上函数值实际是有限的)联合分布。他处理的正是函数分布,把刚才说的难点化为有限观察集上处理。他不管函数是什么样的模型,多项式的还是指数的还是什么的,我们只关心这些函数值是服从联合分布的来进行预测求解,这就是函数空间的无限到有限个观察集上的妙处。高斯过程就是其中一种,其有着良好的一致计算的驯良性,可以理解凡是相似的输入有相似的输出都可以这么处理,尤其是数据量越大越容易把他们的分布极限为高斯联合分布。
这种贝叶斯思想就是:把模型不固定,模型函数的参数认为是不确定,然后把这些不确定(模型即函数值,和决定具体模型函数的参数)都假设为概率分布,而观察到的数据结果是确定唯一的思想。最大后验估计到贝叶斯估计(具体的分布)
传统的函数思想:假定一个确定的模型(比如线性函数),函数参数是未知的但是确定性的,只是我们不知道待求解,最小化损失函数得出参数(一般都是均方误差等,比如最小二乘法)。
传统统计学的思想:模型函数是确定的,参数未知但是确定性的,是一个未知的确定数。但是输出结果是不确定的,即通常说的观察是有误差的,一般认为是高斯误差,所以输出是一个以真实函数值为期望的分布。即观察到的样本数据是不确定但是是最有可能的,我们做的就是把最有可能生成这些数据样本的参数求出来,比如最大似然估计。
以上模型就是函数,函数的输入输出就是样本数据x y,确定与不确定分别指是未知参数,不确定指他不是个参数而是一个分布,是概率上的意义,我们求得是这个数的期望值和置信度(方差)。
所以容易理解原文里提到神经网络无限的时候等价高斯过程回归,
贝叶斯模型的图解

a是先验的四个采样分布的图,b是有两个采样点后的后验,实线是均值的分布,阴影是两个标准差
可以看到,先验图在随机采样下仍然是光滑的,后验图在接近数据点时方差会减小。先验是具有光滑性和静态性(不正式的理解为函数值在任意x位置都是相似的接近的,差不多就是先验不了解函数信息情况下认为函数值大致都在某个数字E(f)附近分布,与x无关)。先验均值函数一般假设为0(可理解为函数取任何值概率是对等的,因为没有更多信息,0就是相当于一个0基准),所以函数四条图像在固定的x值处的平均值趋近于0.这些变化特征都是有方差函数确定,所以高斯过程学习可理解为找到合适性质的方差函数。另外高斯过程回归】是一个非参数模型,所以不大会过拟合,这里可以认为是因为有函数先验分布的正则化(惩罚项)起作用(太过于远离先验的会被拒绝)。关于【高斯过程分类】可以将函数挤压到[0 1]区间,比如通过logstic函数映射为取某类的概率。如图1.2给出二维数据的二分类
高斯过程回归
高斯过程在函数空间来看,可以理解为是关于函数的分布;在权值观点来看可以认为是各函数的加权求和。
2.1权值观点
标准的线性模型可以理解为; f ( x ) = x T w , y = f ( x ) + ϵ 一 般 认 为 ϵ N ( 0 , σ n 2 ) f(x)=\bm{x^Tw},y=f(x)+\epsilon一般认为\epsilon~N(0,\sigma_n^2) f(x)=xTw,y=f(x)+ϵ一般认为ϵ N(0,σn2)
其中似然分布函数为:
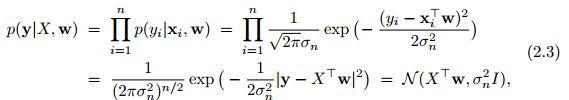
我们假定 w N ( 0 , σ p ) \bm{w~N(0,\sigma_p)} w N(0,σp)根据贝叶斯规则:
p ( w ∣ y , X ) = p ( y ∣ X , w ) p ( w ) p ( y ∣ X ) \bm{p(w|y,X)=\frac{p(y|X,w)p(w)}{p(y|X)}} p(w∣y,X)=p(y∣X)p(y∣X,w)p(w)
分母是边缘似然函数,一般是起归一化作用,为; p ( y ∣ X ) = ∫ p ( y ∣ X , w ) p ( w ) d w \bm{p(y|X)=\int p(y|X,w)p(w)dw} p(y∣X)=∫p(y∣X,w)p(w)dw
可以看到后验是把先验和似然结合起来,似然函数是拟合数据,先验则是一种防止过拟合的惩罚项或者正则项,由上式后验为
p ( w ∣ y , X ) ∝ e x p ( − 1 σ n 2 ( y − X T w ) ( y − X T w ) ) e x p ( − 1 2 w T σ p − 1 w ) ∝ e x p ( − 1 2 ( w − w ˉ ) A ( w − w ˉ ) ) − − − 2.4 \bm{p(w|y,X)\varpropto exp(-\frac{1}{\sigma_n^2}(y-X^Tw)(y-X^Tw))exp(-\frac{1}{2}w^T\sigma_p^{-1}w)} \\ \!\varpropto exp(-\frac{1}{2}(w-\bar w )A(w-\bar w))---2.4 p(w∣y,X)∝exp(−σn21(y−XTw)(y−XTw))exp(−21wTσp−1w)∝exp(−21(w−wˉ)A(w−wˉ))−−−2.4
这里 A = σ n − 2 X X T + σ p − 1 , w ˉ = σ n − 2 A − 1 X y A=\sigma_n^{-2}XX^T+\sigma_p^{-1},\bar w=\sigma_n^{-2}A^{-1}Xy A=σn−2XXT+σp−1,wˉ=σn−2A−1Xy,也就是后验分布为
p ( w ∣ X , y ) ∼ N ( w ˉ , A − 1 ) − − 2.5 p(w|X,y)\sim N(\bar w,A^{-1}) --2.5 p(w∣X,y)∼N(wˉ,A−1)−−2.5
可以看到这里max 式2.5就是最大后验估计,max 式子2.3就是最大似然估计等效于最小均方误差(最小二乘),这里矩阵可能不逆所以通常最小二乘都用迭代的方法。后验里A加入了先验的约束项,所以一定程度防止了过拟合。也可以指直接从2.4第一行看,去-log后极小化,我们看到目标函数有两项,第一项也就是第一个指数项是最大似然函数,第二项 − 0.5 w T σ p − 1 w -0.5w^T\sigma_p^{-1}w −0.5wTσp−1w就类似于我们所说的正则惩罚项。有一个例子就是【岭回归】。
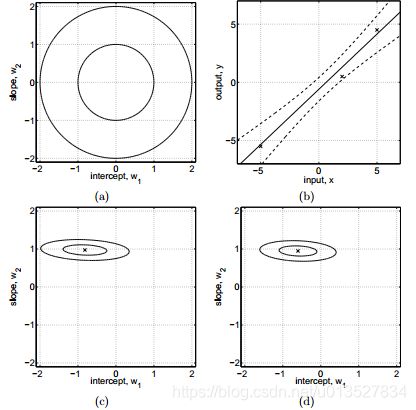
a为参数服从高斯分布的先验图,b为有3个样点后的直线估计,虚线为方差,c,d为有样本点后的参数后验分布图。
预测 x ∗ x_* x∗为
p ( y ∗ ∣ x ∗ , X , y ) = ∫ p ( y ∗ ∣ x ∗ , w ) p ( w ∣ X , y ) d w = N ( σ n − 2 x ∗ T A − 1 X y , x ∗ T A − 1 x ∗ ) \bm{p(y_*|x_*,X,y)=\int p(y_*|x_*,w)p(w|X,y)dw}\\ =N(\sigma_n^{-2}x_*^TA^{-1}Xy , x_*^TA^{-1}x_* ) p(y∗∣x∗,X,y)=∫p(y∗∣x∗,w)p(w∣X,y)dw=N(σn−2x∗TA−1Xy,x∗TA−1x∗)
我们把输入投影到特征空间
比如多项式用线性模型,就要进行特征映射 x : ϕ ( x ) = [ 1 , x , x 2 , x 3 . . . ] T x:\phi(x)=[1,x,x^2,x^3 ...]^T x:ϕ(x)=[1,x,x2,x3...]T定义 Φ \Phi Φ为标量的特征函数 p h i ( x ) phi(x) phi(x)对所有x的结果矩阵(核函数矩阵,方差矩阵),那么
f ( x ) = ϕ ( x ) T w f(x)=\phi(x)^Tw f(x)=ϕ(x)Tw
f ∗ ∣ x ∗ , X , y ∼ N ( σ n − 2 ϕ ∗ T A − 1 Φ y , ϕ ∗ T A − 1 ϕ ∗ ) , h e r e ϕ ∗ = ϕ ( x ∗ ) \bm{f_*|x_*,X,y\sim N(\sigma_n^{-2}\phi_*^TA^{-1}\Phi y , \phi_*^TA^{-1}\phi_* )},here \phi_*=\phi(x_*) f∗∣x∗,X,y∼N(σn−2ϕ∗TA−1Φy,ϕ∗TA−1ϕ∗),hereϕ∗=ϕ(x∗)
这里 A = σ n − 2 Φ Φ T + σ p − 1 , Φ = Φ ( X ) A=\sigma_n^{-2}\Phi\Phi^T+\sigma_p^{-1},\Phi=\Phi(X) A=σn−2ΦΦT+σp−1,Φ=Φ(X)
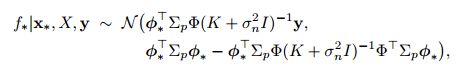
其中 K = Φ T σ p Φ \bm{K=\Phi^T\sigma_p\Phi} K=ΦTσpΦ
注意到,我们的计算只是把 x ∗ − > ϕ ( x ∗ ) , X − > Φ ( X ) \bm{x_* -> \phi(x_*) ,X ->\Phi(X)} x∗−>ϕ(x∗),X−>Φ(X)而且所有的计算都转化成了
ϕ ∗ σ p ϕ ∗ \phi_*\sigma_p\phi_* ϕ∗σpϕ∗可能是大phi也可能小phi,定义
k ( x , x ′ ) = ϕ ( x ) T σ p ϕ ( x ) k(x,x')=\phi(x)^T\sigma_p\phi(x) k(x,x′)=ϕ(x)Tσpϕ(x)
这就是核函数技巧,往往直接用这种k函数计算比原来的计算更高效。
2.2函数空间观点
【高斯过程】定义为一串随机变量的集合,任意有限个这些随机变量组成联合高斯分布。
我们从联合分布,边缘分布,似然函数,先验分布来推导出后验分布也就是条件分布。
假设 y = [ y 1 , y 2 ] T , μ = [ μ 1 ; μ 2 ] , y 1 ∼ N ( μ 1 , k 11 ) , y 2 ∼ N ( μ 2 , k 22 ) y=[y1, y2]^T,\mu=[\mu_1;\mu_2],y1\sim N(\mu_1,k11),y2\sim N(\mu_2,k22) y=[y1,y2]T,μ=[μ1;μ2],y1∼N(μ1,k11),y2∼N(μ2,k22)联合分布为:
y ∼ N ( μ , [ k 11 k 12 k 21 k 22 ] ) y\sim N(\mu,\begin{bmatrix} k11 & k12 \\ k21 & k22 \\ \end{bmatrix}\quad) y∼N(μ,[k11k21k12k22])
或者在我们这里预测模型里y1-x1表示已知的样本数据y2 为我们想要预测的x2 (x*)的值此时y2变成一维的了。那么可以写作
y ∗ = f ( x ∗ ) + ϵ ∼ N ( μ ∗ , k ( x ∗ , x ∗ ) + σ 2 I ) y_*=f(x_*)+\epsilon \sim N(\mu_*,k(x_*,x_*)+\sigma^2I) y∗=f(x∗)+ϵ∼N(μ∗,k(x∗,x∗)+σ2I)
这里把观测噪声已经加上去了,k**相当于k22,一般我们在没过多先验知识下都是假设均值期望为0即 μ = 0 \mu=0 μ=0
那么可以通过贝叶斯规则,即在知道y y1 y2各自分布和联合分布下求条件分布:
p ( y 2 ∣ y 1 ) = p ( y ) p ( y 1 ) = p ( y 1 ∣ y 2 ) p ( y 2 ) p ( y 1 ) p(y2|y1)=\frac{p(y)}{p(y1)}=\frac{p(y1|y2)p(y2)}{p(y1)} p(y2∣y1)=p(y1)p(y)=p(y1)p(y1∣y2)p(y2)
有2种代数方法求解后验条件分布
- 根据分布一致性,大家都是高斯分布,然后对指数项进行配方观察二次项一次项和常数项的系数来确定正态分布的p(y2|y1)的均值和方差(详见prml书里的推导)
- 也有根据分布都是高斯分布的特点,打洞技巧(有点逗结果的味道)或者直接通过引理,推导:
[ A B C D ] − 1 = [ ( A − B D − 1 C ) − 1 − ( A − B D − 1 C ) − 1 − D − 1 C ( A − B D − 1 C ) − 1 D − 1 + D − 1 C ( A − B D − 1 C ) B D − 1 ] { \begin{bmatrix} A & B \\ C & D \\ \end{bmatrix}\quad}^{-1}=\begin{bmatrix} (A-BD^{-1}C)^{-1} & -(A-BD^{-1}C)^{-1}\\ -D^{-1}C(A-BD^{-1}C)^{-1} & D^{-1}+D^{-1}C(A-BD^{-1}C)BD^{-1} \\ \end{bmatrix}\quad [ACBD]−1=[(A−BD−1C)−1−D−1C(A−BD−1C)−1−(A−BD−1C)−1D−1+D−1C(A−BD−1C)BD−1]
都能得到
f ∗ ∣ x ∗ , X , y ∼ N ( μ ∗ ∣ N , σ ∗ ∣ N 2 ) \bm{f_*|x_*,X,y\sim N(\mu_{*|N},\sigma_{*|N}^2)} f∗∣x∗,X,y∼N(μ∗∣N,σ∗∣N2)
μ ∗ ∣ N = μ ∗ + K ( x ∗ , X ) ( K ( X , X ) + σ 2 I ) − 1 ( y N − μ N ) \mu_{*|N}=\mu_*+K(x_*,X)(K(X,X)+\sigma^2I)^{-1}(y_N-\mu_N) μ∗∣N=μ∗+K(x∗,X)(K(X,X)+σ2I)−1(yN−μN)
σ ∗ ∣ N 2 = K ( x ∗ , x ∗ ) + σ 2 I − K ( x ∗ , X ) ( K ( X , X ) + σ 2 I ) − 1 K ( X , x ∗ ) \sigma_{*|N}^2=K(x_*,x_*)+\sigma^2I-K(x_*,X)(K(X,X)+\sigma^2I)^{-1}K(X,x_*) σ∗∣N2=K(x∗,x∗)+σ2I−K(x∗,X)(K(X,X)+σ2I)−1K(X,x∗)
这里N指的就是y1已知N个数据的意思,*就是预测相当于y2的意思,下标都是条件预测,条件分布的意思就是知道N个数据下对先验 p ( y ∗ ) o r p ( y 2 ) p(y_*)or p(y2) p(y∗)orp(y2)修正分布预测的意思。为方便书写,之后都约定或者简写为:
K ∗ = K ∗ N = K ( x ∗ , x N ) , μ ∗ = μ ∗ ∣ N K_*=K_{*N}=K(x_*,x_N),\mu_*=\mu_{*|N} K∗=K∗N=K(x∗,xN),μ∗=μ∗∣N以此类推。
那么我还可以把上式写作(一般先验假定均值 μ ∗ \mu_* μ∗为0):
μ ∗ = K ∗ T α \mu_*=K_*^T\alpha μ∗=K∗Tα or μ ∗ = β y \mu_*=\beta y μ∗=βy
也就是我们既可以看作输出预测为数据y的线性组合也可以看作是核函数的线性组合,所以高斯过程和贝叶斯线性模型是等价的
原文还提到联合分布与独自分布都属于高斯分布的情形也就是大的变量集合的分布不会改变小的子集的分布,就是不管有多少数据服从联合高斯,子集y1或者y2等服从的分布不变。另外SE方差核函数等价于无限基函数的贝叶斯线性回归模型。
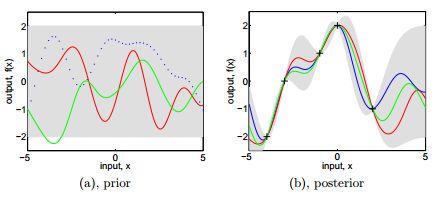
a为先验的高斯联合分布的采样,b为有几个采样点后的后验分布。
GPR算法流程
综上,我们得到GPR算法流程,这和其对应的matlab-tool里gp.m是一致的

其中 f ∗ f_* f∗对应无观测噪声的情况,那样实际观测值 y ∗ = f ∗ + ϵ , ϵ ∼ N ( 0 , σ n 2 ) y_*=f_*+\epsilon,\epsilon\sim N(0,\sigma_n^2) y∗=f∗+ϵ,ϵ∼N(0,σn2)参数估计采用似然估计(核函数里面还是有参数,尽管我们已经用了先验联合分布的高斯过程还是会有参数),一般最小化其负对数的似然函数为
l o g ( p ( y ∣ X ) ) = − 1 2 y T ( K + σ n 2 I ) − 1 y − 0.5 l o g ∣ K + σ n 2 I ∣ − 0.5 N l o g ( 2 π ) log(p(y|X))=-\frac{1}{2}y^T(K+\sigma_n^2I)^{-1}y-0.5log|K+\sigma_n^2I|-0.5Nlog(2\pi) log(p(y∣X))=−21yT(K+σn2I)−1y−0.5log∣K+σn2I∣−0.5Nlog(2π)
其中算法图里,矩阵求逆采用chol分解会更加数值稳定精确和速度更快,其中第2行chol分解 O ( 1 6 N 3 ) O(\frac{1}{6}N^3) O(61N3)第3行第5行为 O ( 0.5 N 2 ) O(0.5N^2) O(0.5N2)
改变超参数
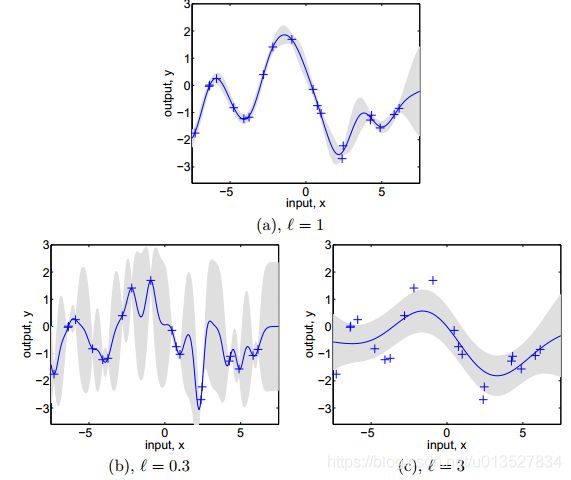
这里核函数为 k ( x , x ′ ) = σ f 2 e x p ( − ( x − x ′ ) 2 2 l ) + σ n 2 δ x x ′ \bm{k(x,x')=\sigma_f^2exp(-\frac{(x-x')^2}{2l})+\sigma_n^2\delta_{xx'}} k(x,x′)=σf2exp(−2l(x−x′)2)+σn2δxx′delta函数为当x=x’时取1否则为0.
这里简单说一下,lenth-scale也就是L影响着函数的摆动,他相当于半径 r = ∣ x − x ′ ∣ r=|x-x'| r=∣x−x′∣的尺度缩放因子,其越小,函数摆动越大,而且倾向于将观测噪声 σ n \sigma_n σn方差拉小。太大就反之变化缓慢,可以理解为x要变化很大才算变化否则就像当于x x’很近没变化。
决策理论
非贝叶斯方法中通常都用经验损失函数或者经验风险函数来决策出最佳预测值,贝叶斯则用似然函数(用于训练集,不含先验)决策,明显截然不同。似然函数描述了相对于真实函数值的噪声测度(噪声影响多少)。
通常我们都用最小化期望损失函数决策函数来给出最终的关于x*的最佳猜测值即y_guess(这里不仅仅有释然函数还加上了传统的决策函数)
m i n : E l o s s = ∫ l o s s ( y ∗ , y g u e s s ) p ( y ∗ ∣ x ∗ , X , y ) d y ∗ min:E_loss=\int loss(y_*,y_{guess})p(y_*|x_*,X,y)dy_* min:Eloss=∫loss(y∗,yguess)p(y∗∣x∗,X,y)dy∗
通常loss函数选择为 0.5 ∣ y ∗ − y g u e s s ∣ o r ( y ∗ − y g u e s s ) 2 0.5|y_*-y_{guess}|or(y_*-y_{guess})^2 0.5∣y∗−yguess∣or(y∗−yguess)2
对于前者决策函数得出的y_guess为分布 p ( y ∗ ∣ x ∗ , D ) p(y_*|x_*,D) p(y∗∣x∗,D)的中值,后者得到的恰好是 p ( y ∗ ∣ x ∗ , D ) p(y_*|x_*,D) p(y∗∣x∗,D)的均值mu也就是期望。
可以看到二次决策函数下高斯回归得到的期望mu值和传统的二次决策函数的最优值是一致的(最小二乘等价),注意前面推导出的 p ( y ∗ ∣ x ∗ , D ) p(y_*|x_*,D) p(y∗∣x∗,D)是关于输出值的概率分布,期望为 μ \mu μ但是有方差这一置信度,并不代表就是输出值。对于最终的输出去多少为好是根据得到的分布去得到的,这取决于决策(风险)函数怎么选取,参考上面最小化期望风险。一般我们认为取值为期望这是和传统方法里的最小二乘法结果一致的(都选择了二次决策函数情况下),但是贝叶斯的方法还给出了误差估计,即相当于 σ 2 \sigma^2 σ2方差。而且这里举列子说的决策函数是对称的(yy_guess互换位置不变),所以结果必然是和y的分布期望mu有关,而且会是线性有关,取决于决策函数的幂数。但是往往也有不对称的决策函数,比如我们只要大于y的猜测y-guess,比如在涉及安全问题,我们肯定不会要低于期望 μ \mu μ的值,否则后果不可估量。又比如在贝叶斯优化里的EI函数就是expect improvement我们就是只看函数在x点能期望提升多少,不能提升的都是没用的都认为EI=0,这种优化决策也是不对称的。
平滑器的解释
前面有粗布说到高斯过程回归是线性平滑器,我们这里给出初步的理论解释。
f ˉ = μ ∗ = K ∗ N ( K + σ n 2 I ) − 1 y \bar f=\mu_*=K_{*N}(K+\sigma_n^2I)^{-1}y fˉ=μ∗=K∗N(K+σn2I)−1y
对K做【特征值分解】,注意到K对称半正定,特征向量单位正交,特征值非负,容易推导出有
K = ∑ i = 1 n λ i u i u i T \bm{K=\sum_{i=1}^n\lambda_iu_iu_i^T } K=i=1∑nλiuiuiT
令 y = ∑ γ i u i \bm{y=\sum\gamma_iu_i} y=∑γiui可以得到 γ i = u i T y \gamma_i=u_i^Ty γi=uiTy则有
f ˉ = ∑ i n γ i λ i λ i + σ n 2 u i = β i u i \bar f=\sum_i^n\frac{\gamma_i\lambda_i}{\lambda_i+\sigma_n^2}u_i=\beta_iu_i fˉ=∑inλi+σn2γiλiui=βiui
可以看到当系数KaTeX parse error: Expected 'EOF', got '\g' at position 1: \̲g̲_i/(\lambda_i+\…也就是噪声相对大于某特征值时,y在K空间的投影对于特征向量ui的分量趋近于无。特征值小的分量意味着该特征方向频率较大,实际中大多数方差函数就是这样,特征值小对应特征向量变化缓慢即很少穿过零点。特征值小意味着y在k空间的高频分量被平滑掉了(没有了)
平滑器自由度可以定义为: t r ( K ( k + σ n 2 I ) − 1 ) = ∑ ( λ i / ( λ i + σ n 2 ) ) tr(K(k+\sigma_n^2I)^{-1})=\sum(\lambda_i/(\lambda_i+\sigma_n^2)) tr(K(k+σn2I)−1)=∑(λi/(λi+σn2))他数量上相当于没有被平滑掉的特征向量的数量(当特征值都不算太小,相对于噪声,那么上述求和项就近似为1了,所以等价于未被平滑的特征向量的数量)。
再把上式写作 f ˉ = h ( x ∗ ) T y \bar f=h(x_*)^Ty fˉ=h(x∗)Tyh可以被称之为权值函数,他是于y无关的,注意到传统的线性组合模型都是输入x的线性组合,而一个线性平滑器这里就是GPR都是目标值y的线性组合。同时K矩阵只与输入x的位置有关,因此可以说这种平滑处理其实就是把观测密集地方的数据给平滑了,也就是给抹除了。(观测密集的地方,对应着有很多样本数据x y相同或者说非常相似接近,也就是说他们是高频率的对应的k的特征值分量很小)
令 k i = k ( ∣ x i − x ∗ ∣ / l ) , f ˉ ( x ∗ ) = ∑ w i y i , w i = k i / ∑ k j k_i=k(|x_i-x_*|/l), \bar f(x_*)=\sum w_iy_i,w_i=k_i/\sum k_j ki=k(∣xi−x∗∣/l),fˉ(x∗)=∑wiyi,wi=ki/∑kj
上面的k函数是不含噪声的SE核函数,用它和h(x*)权值函数等效就相当于平滑器的等效核函数了。
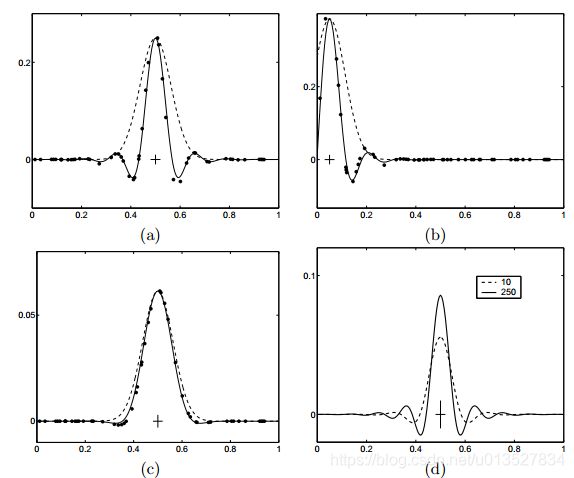
实线是等效核函数(不含噪声),虚线是真实的核函数即 h ( x ∗ ) h ( x ∗ ) T \bm{h(x_*)h(x_*)^T} h(x∗)h(x∗)T,图a,x*=0.5,sn2=0.1图b,x*=0.05,sn2=0.1。图c,sn2=10图d是数据量n增大.可以看到噪声较小是等效核函数剧烈震荡,甚至为负。噪声大的时候等效核函数和实际含噪声的核函数会比较接近,也就实线了平滑化,当区间内数据点增多时,两者都会震荡而且幅度差距会比较大,说明数据取得太密了。可以理解当噪声太小或者数据过密意味着数据更真实更趋向于过拟合样本,所以会抖动。
关于这一点,本人在实验过程中也发现过类似想象不过一直没有理论的解释,一直姑且直观的认为是当噪声较大时其可以添补抹平函数的过小的细节部分(见我的gp存图)。可以想象当数据有重叠或者相似的时候意味着K矩阵的某些行是线性相关的,尽管在加了对角噪声后矩阵可逆了,但是那几行因为线性相关特征向量是一样的,意味着高频,在加权求和过程中会相互抵消。意味着重复雷同的数据将会被视为无效数据噪声越大不仅起到防止矩阵奇异的作用,还保证了数值稳定性和拟合平滑性,某种程度上有防止过拟合作用。这究竟算好事还是坏事呢?一方面这避免了冗余无效数据的干扰,平滑,防止过拟合,另外一方面他会让主要数据无效丢失作用,加入某个系统输入输出本就就都很狭窄相似呢?下图是0.5sin(15x)sin(27x)的预测图,上图sn=0.001,下图是sn=0.6很大,所以太过于平滑即f各处都接近,这样虽然不准确但是也能起到防止局部最优(全局最优点还是没变在0.3附近)
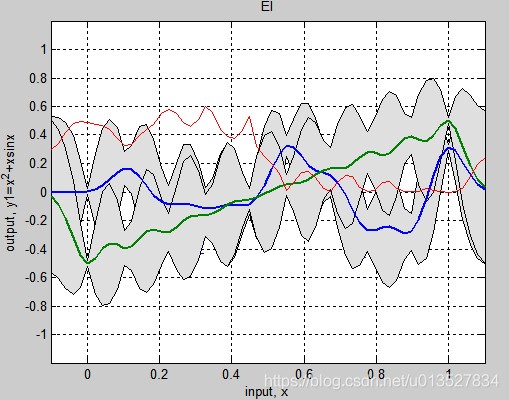
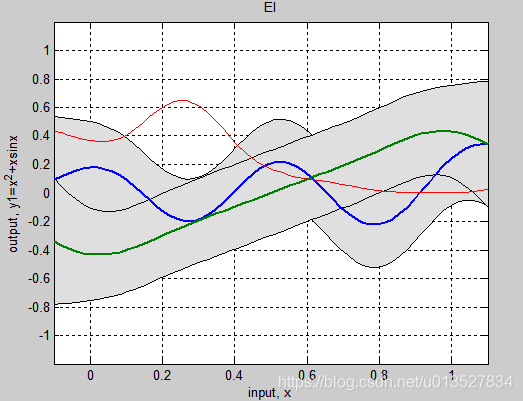
原文还讲到用网格化的方式做等效核函数,不太明白,略了