设计 | 前缀树、字典树、Trie：力扣208. 实现 Trie (前缀树)

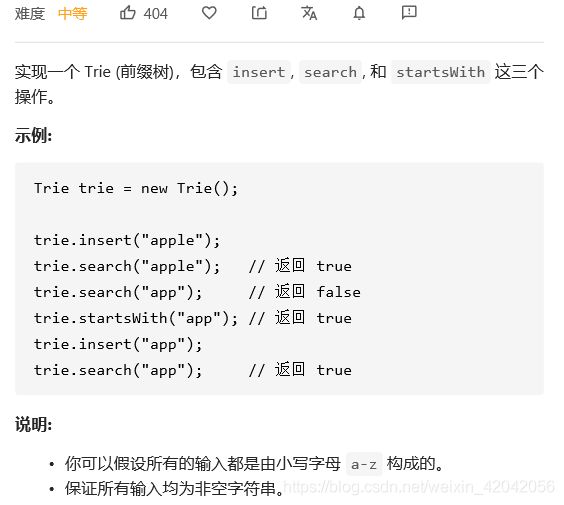
1、题目描述：

2、题解：

插入：insert()
向Trie中插入一个单词word
这个操作和构建链表很像。先检查，找到不到就创建。首先从根结点的子结点开始与 word 第一个字符进行匹配，一直匹配到前缀链上没有对应的字符，
这时开始不断开辟新的结点，直到插入完 word 的最后一个字符，同时还要将最后一个结点isEnd = true;
表示它是一个单词的末尾。

查找：
查找 Trie 中是否存在单词 word
从根结点的子结点开始，一直向下匹配即可，如果出现结点值为空就返回false，如果匹配到了最后一个字符，
那我们只需判断node->isEnd即可。

查找前缀树：
判断 Trie 中是或有以 prefix 为前缀的单词
和 search 操作类似，只是不需要判断最后一个字符结点的isEnd，因为既然能匹配到prefix最后一个字符，那后面一定有单词是以它为前缀的。

Python实现：

class Trie:
    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.lookup = {
     }
    def insert(self, word: str) -> None:
        """
        Inserts a word into the trie.
        """
        tree = self.lookup
        for a in word:
            if a not in tree:
                tree[a] = {
     }
            tree = tree[a]
        #单词结束的标志
        tree['#'] = '#'
    def search(self, word: str) -> bool:
        """
        Returns if the word is in the trie.
        """
        tree = self.lookup
        for a in word:
            if a not in tree:
                return False
            tree = tree[a]
        if '#' in tree:
            return True
        return False
    def startsWith(self, prefix: str) -> bool:
        """
        Returns if there is any word in the trie that starts with the given prefix.
        """
        tree = self.lookup
        for a in prefix:
            if a not in tree:
                return False
            tree = tree[a]
        return True

# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)

C++实现：

class Trie {
     
private:
    bool isEnd;
    Trie* next[26];
public:
    /** Initialize your data structure here. */
    Trie() {
     
        isEnd = false;
        memset(next,0,sizeof(next));
    }
    
    /** Inserts a word into the trie. */
    void insert(string word) {
     
        Trie* node = this;
        for (char c : word){
     
            if (node->next[c - 'a'] == NULL){
     
                node->next[c - 'a'] = new Trie();
            }
            node = node->next[c - 'a'];
        }
        node->isEnd = true;
    }
    
    /** Returns if the word is in the trie. */
    bool search(string word) {
     
        Trie* node = this;
        for (char c : word){
     
            node = node->next[c - 'a'];
            if (node == NULL){
     
                return false;
            }
        }
        return node->isEnd;
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
     
        Trie* node = this;
        for (char c : prefix){
     
            node = node->next[c - 'a'];
            if (node == NULL){
     
                return false;
            }
        }
        return true;
    }
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */

3、复杂度分析：

插入：
时间复杂度：O(m)，m为键长，要么检查要么创建一个节点，直到到达键尾，只需要m次操作
空间复杂度：O(m),最坏的情况下，新插入的键和Trie树中已有的键没有公共前缀，此时需要添加m个节点。
查找：
时间复杂度：O(m),算法每一步均搜索下一个键字符，最坏的情况下需要m次操作
空间复杂度：O(1)
查找前缀树：
时间复杂度：O(m)
空间复杂度：O(1)