python常用模块(二) —— numpy
参考视频视频:黑马Python教程4天快速入手Python数据挖掘
切片图片出自:https://www.jianshu.com/p/a380222a3292
1 Numpy优势
1.1 Numpy介绍
- Numpy(Numerical Python)是一个开源的Python科学计算库,用于快速处理任意维度的数组。(numerical → \to → 数值化的)
- Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务,使用Numpy比直接使用Python要简洁的多。
- Numpy使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。
1.2 ndarray介绍
NumPy provides an N-dimensional array type, the ndarray, which describes a collection of “item” of the same type.
NumPy提供了一个N维数组类型ndarray,描述了相同类型的“items”的集合。
ndarray:n → \to → 任意个;d → \to → dimension 维度;array → \to → 数组
import numpy as np
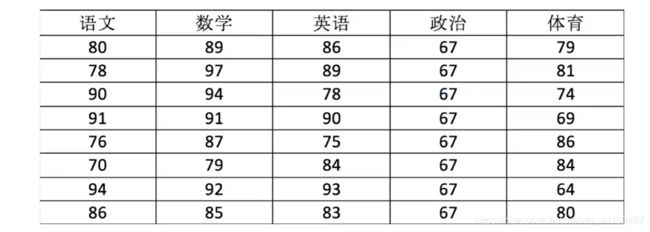
score = np.array([[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]]) # 将数据存储到 ndarray容器中In[1] :score
Out[1]: array([[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])In[1] :type(score)
Out[1]: numpy.ndarray 1.3 ndarray与Python原生list运算效率对比
使用 Python列表可以存储一维数组,通过列表的嵌套可以实现多维数组。
那么为什么还需要使用 Numpy的ndarray呢?
import random
import time
# 生成一个大数组
python_list = []
for i in range(100000000):
python_list.append(random.random())
ndarray_list = np.array(python_list)# 原生pythonlist求和
t1 = time.time()
a = sum(python_list)
t2 = time.time()
d1 = t2 - t1 # 0.7309620380401611
# ndarray求和
t3 = time.time()
b = np.sum(ndarray_list)
t4 = time.time()
d2 = t4 - t3 # 0.12980318069458008总结:
- 从中可以看到ndarray的计算速度要快很多,节约了时间。
- 机器学习的最大特点就是大量的数据运算,如果没有一个快速的解决方案,那可能现在 python也在机器学习领域达不到好的效果。
- Numpy专门针对ndarray的操作和运算进行了设计,所以数组的存储效率和输入输出性能远优于Python中的嵌套列表,数组越大,Numpy的优势就越明显。
1.4 ndarray的优势
-
内存块风格:ndarray - 相同类型 - 通用性不强;list - 不同类型 - 通用性很强。
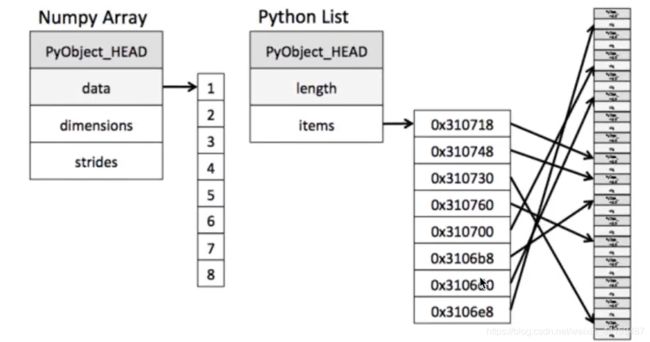
从图中可以看岀ndarray在存储数据的时候,数据与数据的地址都是连续的,这样使得批量操作数组元素时速度更快。
因为ndarray中的所有元素的类型都是相同的,而Python列表中的元素类型是任意的,所以ndarray在存储元素时内存可以连续,而python原生list就只能通过寻址方式找到下一个元素,这虽然导致了在通用性能方面Numpy的ndarray不及Python原生list,但在科学计算中,Numpy的ndarray就可以省掉很多循环语句,代码使用方面比 Python原生list简单的多。 -
ndarray支持并行化运算(向量化运算)。
-
Numpy底层使用c语言编写,内部解除了GIL(全局解释器锁),其对数组的操作速度不受 Python解释器的限制,效率远高于纯 Python代码。
2 N维数组 - ndarray
2.1 ndarray的属性
| 属性名字 | 属性解释 |
|---|---|
| ndarray.shape | 数组维度的元组 |
| ndarray.ndim | 数组维数 |
| ndarray.size | 数组中的元素数量 |
| ndarray.dtype | 数组元素的类型 |
| ndarray.itemsize | 一个数组元素的长度(字节) |
In[1] :score.shape
Out[1]: (8, 5) # 8行5列,元组表示
In[1] :score.ndim
Out[1]: 2 # 2维
In[1] :score.size
Out[1]: 40 # 40个元素
In[1] :score.dtype
Out[1]: dtype('int64') # 默认整数类型
In[1] :score.itemsize
Out[1]: 8 # 一个元素 8 个字节2.2 ndarray的形状
# 首先创建一些数组:
a = np.array([[1,2,3],[4,5,6]])
b = np.array([1,2,3,4])
c = np.array([[[1,2,3],[4,5,6]],[[1,2,3],[4,5,6]]])In[1] :a
Out[1]: array([[1, 2, 3],
[4, 5, 6]])
In[1] :a.shape
Out[1]: (2, 3) # 二维数组In[1] :b
Out[1]: array([1, 2, 3, 4])
In[1] :b.shape
Out[1]: (4,) # 一维数组In[1]:c
Out[1]: array([[[1, 2, 3],
[4, 5, 6]],
[[1, 2, 3],
[4, 5, 6]]])
In[1] :c.shape
Out[1]: (2, 2, 3) # 三维数组注意:
- 可以查看最外围中括号,有几个就是几维
- 数组的形状
ndarray.shape用元组表示
2.3 ndarray的类型
dtype是numpy.dtype类型
| 名称 | 描述 | 简写 |
|---|---|---|
| np.bool | 用一个字节存储的布尔类型(True或 False) | ‘b’ |
| np.int8 | 一个字节大小,-128至127 | ‘i’ |
| np.int16 | 整数,-32768至32767 | ‘i2’ |
| np.int32 | 整数,-231至232-1 | ’i4’ |
| np.int64 | 整数,-263至263-1 | ’i8’ |
| np.uint8 | 无符号整数,0至255 | ’u’ |
| np.uint16 | 无符号整数,0至65535 | ‘u2’ |
| np.uint32 | 无符号整数,0至232-1 | ‘u4’ |
| np.uint64 | 无符号整数,0至264-1 | ‘u8’ |
| np.float16 | 半精度浮点数:16位,正负号1位,指数5位,精度10位 | ‘f2’ |
| np.float32 | 单精度浮点数:32位,正负号1位,指数8位,精度23位 | ’f4’ |
| np.float64 | 双精度浮点数:64位,正负号1位,指数11位,精度52位 | ’f8’ |
| np.complex64 | 复数,分别用两个32位浮点数表示实部和虚部 | ‘c8’ |
| np.complex 128 | 复数,分别用两个64位浮点数表示实部和虚部 | ‘c16’ |
| np.object | python对象 | ‘O’ |
| np.string | 字符串 | ‘S’ |
| np. unicode_ | unicode类型 | ‘U’ |
data = np.array([1.1, 2.2, 3.3])
In[1] :data
Out[1]: array([1.1, 2.2, 3.3])
In[1] :data.dtype
Out[1]: dtype('float64') # 默认浮点类型创建数组的时候指定类型:
In[1] :np.array([1.1, 2.2, 3.3], dtype="float32")
Out[1]: array([1.1, 2.2, 3.3], dtype=float32)
In[1] :np.array([1.1, 2.2, 3.3], dtype=np.float32)
Out[1]: array([1.1, 2.2, 3.3], dtype=float32)# 不常用
arr = np.array(['python','tensorflow','scikit-learn', 'numpy'], dtype =np.string_)
In[1] :arr
Out[1]: array([b'python', b'tensorflow', b'scikit-learn', b'numpy'], dtype='|S12')注意: 若不指定,整数默认int64,小数默认foat64。
3 基本操作
ndarray.方法()或者np.函数名()。
3.1 生成数组的方法
3.1.1 生成0和1的数组
- empty(shape[, dtype, order])
empty_like(a[, dtype, order, subok])
eye(N[, M, k, dtype, order]) - identity(n[, dtype)
ones(shape[, dtype, order])- ones_like(a[, dtype, order, subok])
zeros(shape[, dtype, order])
zeros_like(a[, dtype, order, subok])
full(shape, fill_value[, dtype, order])- full_like(a, fill_value, dtype, order, subok])
# 生成 0 的数组
In[1] :np.zeros(shape=(3, 4), dtype="float32")
Out[1]: array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]], dtype=float32)
# 生成 1 的数组
In[1] :np.ones(shape=[2, 3], dtype=np.int32)
Out[1]: array([[1, 1, 1],
[1, 1, 1]], dtype=int32)注意: 查看np.shape属性时,表示方法为元组;指定形状,既可以用元组也可以用列表。
3.1.2 从现有数组生成
array(object[, dtype, copy, order, subok, ndmin])asarray(a[, dtype, order])- asanyarray(a[, dtype, order])
ascontiguousarray(a[, dtype]) - asmatrix(data[, dtype)
copy[a[, order]
关于 array 和 asarray 的不同
a = np.array([[1, 2, 3], [4, 5, 6]])
In[1] :a
Out[1]: array([[1, 2, 3],
[4, 5, 6]])- np.array( ),从现有的数组当中创建
a1 = np.array(a)
In[1] :a1
Out[1]: array([[1, 2, 3],
[4, 5, 6]])- np.asarray( ),相当于索引的形式,并没有真正的创建一个新的
a2 = np.asarray(a)
In[1] :a2
Out[1]: array([[1, 2, 3],
[4, 5, 6]])- np.copy()
a3 = np.copy(a)
In[1] :a3
Out[1]: array([[1, 2, 3],
[4, 5, 6]])总结: a1 = np.array(a),a2 = np.asarray(a),a3 = np.copy(a)三者数据显示相同
改数值:
a[1, 1] = 1000
In[1] :a
Out[1]: array([[ 1, 2, 3],
[ 4, 1000, 6]])- a1 = np.array(a),数据未改,深拷贝
In[1] :a1
Out[1]: array([[1, 2, 3],
[4, 5, 6]])- a2 = np.asarray(a),数据改变,浅拷贝
In[1] :a2
Out[1]: array([[ 1, 2, 3],
[ 4, 1000, 6]])- a3 = np.copy(score),数据未改,深拷贝
In[1] :data3
Out[1]: array([[1, 2, 3],
[4, 5, 6]])3.1.3 生成固定范围的数组
np.linspace(start, stop, num, endpoint, retstep, dtype)
生成等间隔的序列
- start 序列的起始值
- stop 序列的终止值
- 如果 endpoint 为true,该值包含于序列中,默认闭区间
[ ]
- 如果 endpoint 为true,该值包含于序列中,默认闭区间
- num要生成的等间隔样例数量,默认为50
- endpoint 序列中是否包含 stop 值,默认为ture
- retstep 如果为 true,返回样例以及连续数字之间的步长
- dtype输出 ndarray的数据类型
In[1] :np.linspace(0, 10, 5)
Out[1]: array([ 0. , 2.5, 5. , 7.5, 10. ])numpy.arange(start, stop, step, dtype),左闭右开[ ),step是步长
In[1] :np.arange(0, 10, 5)
Out[1]: array([ 0, 5])numpy.logspace(start, stop, num, endpoint, base, dtype),构建等比数列
3.1.4 生成随机数组:np.random模块
1. 均匀分布(Uniform Distribution)
概率统计中的重要分布之一。顾名思义,均匀,表示可能性相等的含义。均匀分布在自然情况下极为罕见,而人工栽培的有一定株行距的植物群落即是均匀分布。
- np.random.rand(d0, d1, … dn),返回 [0.0, 1.0) 内的一组均匀分布的数
np.random.uniform(low=0.0, high=1.0, size=None)- 功能:从一个均匀分布[low,high)中随机采样, 注意定义域是左闭右开
- 参数介绍:
low:采样下界, float类型, 默认值为0;
high:采样上界, float类型, 默认值为1;
size:输出样本数目, 为int或元组(tuple)类型, 例如, size=(m,n,k), 则输出mnk个样本, 缺省时输出1个值。
返回值:ndarray类型, 其形状和参数size中描述一致。
- np.random.randint(low, high=None, size=None, dtype=‘l’)
- 从一个均匀分布中随机采样,生成一个整数或N维整数数组,取数范围:若high不为None时,取[low, high)之间随机整数,否则取值[0, low)之间随机整数。
示例:
data1 = np.random.uniform(low=-1, high=1, size=1000000)
In[1] :data1
Out[1]:array([-0.49795073, -0.28524454, 0.56473937, ..., 0.6141957 ,
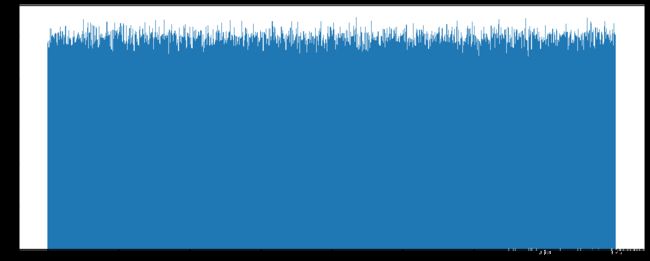
0.4149972 , 0.89473129])画图看分布状况:
import matplotlib.pyplot as plt
# 1、创建画布
plt.figure(figsize=(20, 8), dpi=80)
# 2、绘制直方图
plt.hist(data1, 1000)
# 3、显示图像
plt.show()2. 正态分布
简介:
-
正态分布是一种概率分布,是具有两个参数 μ \mu μ 和 σ \sigma σ 的连续型随机变量的分布,第一个参数 μ \mu μ 是服从正态分布的随机变量的均值,第二个参数 σ \sigma σ 是此随机变量的标准差,所以正态分布记作 N ( μ , σ ) N(\mu, \sigma) N(μ,σ)。
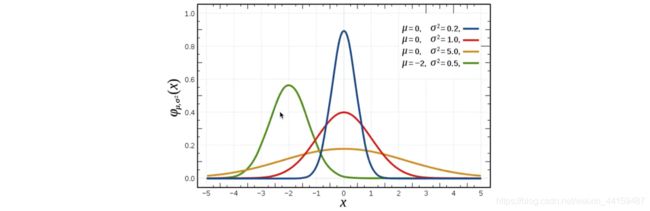
应用:生活、生产与科学实验中很多随机李量的概率分布都可以近似地用正态分布来描述。 -
正态分布特点: μ \mu μ 决定位置,标准差 σ \sigma σ 决定分布的幅度、集中程度。当 μ = 0 \mu=0 μ=0, σ = 1 \sigma=1 σ=1 时的正态分布是标准正态分布。
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=σ2π1e−2σ2(x−μ)2
- 标准差:方差开平方。
方差:
s 2 = ( x 1 − μ ) 2 + ( x 2 − μ ) 2 + ( x 3 − μ ) 2 + … … + ( x n − μ ) 2 n s^2=\frac{(x_1-\mu)^2+(x_2-\mu)^2+(x_3-\mu)^2+……+(x_n-\mu)^2}{n} s2=n(x1−μ)2+(x2−μ)2+(x3−μ)2+……+(xn−μ)2其中 μ \mu μ 为平均值, n n n为数据总个数, s s s 为标准差 σ \sigma σ
σ = 1 N ∑ i = 1 N ( x i − μ ) 2 \sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2} σ=N1i=1∑N(xi−μ)2标准差与方差的意义:在概率论和统计学中衡量一组数据离散程度的度量。
正态分布语法:
- np.random.rand(d0, d1, … dn)
- 功能:从标准正态分布中返回一个或多个样本值
np.random.normal(loc=0.0, scale=1.0, size=None)- loc:float类型,此概率分布的均值(对应着整个分布的中心 centre)
- scale:float类型,此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高)
- size:int or tuple of ints,输出的 shape,默认为None,只输出一个值
- np.random.standard_normal(size=None),返回指定形状的标准正态分布的数组。
示例:
# 正态分布
data2 = np.random.normal(loc=1.75, scale=0.1, size=1000000)
In[1] :data2
Out[1]: array([1.66381498, 1.81276401, 1.58393696, ..., 1.72017482, 1.90260969,
1.69554529])图像显示效果:
# 1、创建画布
plt.figure(figsize=(20, 8), dpi=80)
# 2、绘制直方图
plt.hist(data2, 1000)
# 3、显示图像
plt.show()3.2 数组操作
案例:随机生成8只股票2周的交易日涨跌幅数据
- 两周的交易日数量为:2×5=10天
- 随机生成涨跌幅在某个正态分布内,比如均值0,方差1
3.2.1 股票涨跌幅数据的创建
stock_change = np.random.normal(loc=0, scale=1, size=(8, 10))
In[1] :stock_change
Out[1]: array([[-0.03469926, 1.68760014, 0.05915316, 2.4473136 , -0.61776756,
-0.56253866, -1.24738637, 0.48320978, 1.01227938, -1.44509723],
[-1.8391253 , -1.10142576, 0.09582268, 1.01589092, -1.20262068,
0.76134643, -0.76782097, -1.11192773, 0.81609586, 0.07659056],
...
[-2.93762047, 0.22199761, 0.98788788, 0.37899235, 0.28281886,
-1.75837237, -0.09262863, -0.92354076, 1.11467277, 0.76034531],
[-0.39473551, 0.28402164, -0.15729195, -0.59342945, -1.0311294 ,
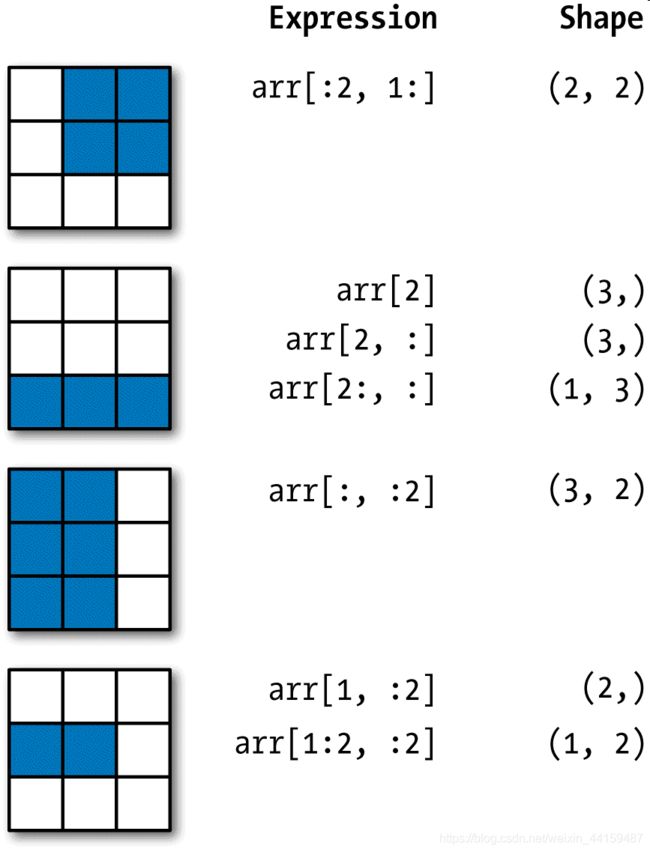
-1.07651428, 0.18618331, 1.5780439 , 1.31285558, 0.10777784]])3.2.2 数组的索引、切片
获取第一个股票的前3个交易日的涨跌幅数据
# 二维的数组,两个维度
In[1] :stock_change[0, :3]
Out[1]: array([-0.03469926, 1.68760014, 0.05915316])一维、二维、三维的数组索引:
# 三维,一维
a1 = np.array([[[1,2,3],[4,5,6]], [[12,3,34],[5,6,7]]])
In[1] :a1
Out[1]: array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[12, 3, 34],
[ 5, 6, 7]]])
# 索引、切片
In[1] :a1[0, 0, 1]
Out[1]: 2
# 形状
In[1] :a1.shape
Out[1]: (2, 2, 3)
# 值修改
a1[1, 0, 2] = 100000
In[1] :a1
Out[1]: array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 12, 3, 100000],
[ 5, 6, 7]]])3.3.3 形状修改 - 转置
需求:将上述股票行、日期列反过来,变成日期行,股票列
ndarray.reshape(shape[, order]):returns an array containing the same data with a new shape.
# 在转换形状的时候,一定要注意数组的元素匹配
stock_change.reshape([-1, 201]) # 数组的形状被修改为:(4, 20),-1:表示待计算In[1] :stock_change.reshape((10, 8)) # stock_change.reshape([10, 8])
Out[1]: array([[-0.03469926, 1.68760014, 0.05915316, 2.4473136 , -0.61776756,
-0.56253866, -1.24738637, 0.48320978], # 一行 8 个数据
[ 1.01227938, -1.44509723, -1.8391253 , -1.10142576, 0.09582268,
1.01589092, -1.20262068, 0.76134643],
...........])
# 原始数据没有改变
In[1] :stock_change
Out[1]: array([[-0.03469926, 1.68760014, 0.05915316, 2.4473136 , -0.61776756,
-0.56253866, -1.24738637, 0.48320978, 1.01227938, -1.44509723],
[-1.8391253 , -1.10142576, 0.09582268, 1.01589092, -1.20262068,
0.76134643, -0.76782097, -1.11192773, 0.81609586, 0.07659056],
............])总结:
- ndarray.reshape(shape)只是将形状进行了修改,并没有将行列进行转换,原始数据按行读取,从左至右,依次读取8个数据,共10次 → \to → 10行8列。
- ndarray.reshape(shape) 返回新的ndarray,原始数据没有改变。
ndarray.resize(new_shape[, refcheck]):Change shape and size of array in-place.
In[1]:stock_change.resize((10, 8))
In[1] :stock_change.shape
Out[1]: (10, 8)
In[1] :stock_change
Out[1]: array([[-0.03469926, 1.68760014, 0.05915316, 2.4473136 , -0.61776756,
-0.56253866, -1.24738637, 0.48320978]
[1.01227938, -1.44509723, -1.8391253 , -1.10142576, 0.09582268,
1.01589092, -1.20262068, 0.76134643],
............]) 总结:
- ndarray.resize(shape) 只是将形状进行了修改,并没有将行列进行转换,原始数据按行读取,从左至右,依次读取8个数据,共10次 → \to → 10行8列。
- ndarray.resize(shape) 没有返回值,对原始的ndarray进行了修改。
ndarray.T数组的转置:将数组的行、列进行互换
In[1] :stock_change.T
Out[1]: array([[-0.03469926, -1.8391253 , -0.74293074, 0.45914676, -0.50413407,
0.3627785 , -2.93762047, -0.39473551],
[ 1.68760014, -1.10142576, -0.7836588 , -0.78330377, -1.35848099,
1.00279706, 0.22199761, 0.28402164],
............])总结:
- ndarray.T将数组的行、列进行互换。
- ndarray.T 返回新的ndarray,原始数据没有改变。
3.3.4 类型修改
ndarray.astype(type):更改数组类型
# 浮点型 ndarray 转化为整型
In[1] :stock_change.astype("int32")
Out[1]: array([[ 0, 1, 0, 2, 0, 0, -1, 0, 1, -1],
[-1, -1, 0, 1, -1, 0, 0, -1, 0, 0],
[ 0, 0, 1, 0, 1, 2, 0, 0, 0, 0],
[ 0, 0, -1, 0, 0, -1, 0, -1, 0, 0],
[ 0, -1, -2, -1, 0, 0, 0, 1, 1, 0],
[ 0, 1, 0, -2, -2, -1, 1, -2, 1, 1],
[-2, 0, 0, 0, 0, -1, 0, 0, 1, 0],
[ 0, 0, 0, 0, -1, -1, 0, 1, 1, 0]], dtype=int32)ndarray.tostring([order])或者ndarray.tobytes([order]):Construct Python bytes containing the raw data bytes in the array.(ndarray序列化到本地)
概念:把对象或者结构体从内存中变成可存储或传输的过程称之为序列化。序列化是将一个对象转换成字节流(byte[ ],或者叫字符串,2进制串)以达到将其长期保存在内存、数据库或文件中的处理过程。它的主要目的是保存对象的状态以便以后需要的时候使用。
In[1] :stock_change.tostring()
Out[1]: b'\x95&\x99\xdd\x19\xc4\xa1\.......\xa2\x95x&\x19\x94\x03@\x9f?\x8c\x98P\xdbt\x01\xf5?t\xd8 -T\x97\xbb?'3.3 数组的去重
语法:np.unique(ndarray)
temp = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])
In[1] :temp
Out[1]: array([[1, 2, 3, 4],
[3, 4, 5, 6]])
# 方法一:
In[1] :np.unique(temp)
Out[1]: array([1, 2, 3, 4, 5, 6])
# 方法二:
In[1] :temp.flatten() # 平滑处理
Out[1]: array([1, 2, 3, 4, 3, 4, 5, 6])
In[1] :set(temp.flatten()) # 集合去重,集合只能处理一维形式
Out[1]: {
1, 2, 3, 4, 5, 6}4 ndarray运算
4.1 逻辑运算
操作符合某一条件的数据。
4.1.1 逻辑判断
stock_change = np.random.normal(loc=0, scale=1, size=(5, 5))
In[1] :stock_change
Out[1]: array([[ 1.46338968, -0.45576704, 0.29667843, 0.16606916, 0.46446682],
[ 0.36775845, 0.24078108, 0.122042 , 1.19314047, 1.34072589],
[-1.48252741, -0.69347186, 0.91122464, -0.30606473, 0.41598897],
[ 0.39438905, -1.31770556, 1.7344868 , -1.52812773, -0.47703227],
[-0.9822216 , -1.09482936, -0.81834523, 0.57335311, 0.97390091]])
# 逻辑判断, 如果涨跌幅大于0.5就标记为True,否则为False
In[1] :stock_change > 0.5
Out[1]: array([[ True, False, False, False, False],
[False, False, False, True, True],
[False, False, True, False, False],
[False, False, True, False, False],
[False, False, False, True, True]])
# 判断 stock_change[0:2, 0:5]是否全是上涨的
In[1] :stock_change[0:2, 0:5] > 0
Out[1]: array([[ True, False, True, True, True],
[ True, True, True, True, True]])4.1.2 布尔索引
In[1] :stock_change[stock_change > 0.5] = 1.1
In[1] :stock_change
Out[1]: array([[ 1.1 , -0.45576704, 0.29667843, 0.16606916, 0.46446682],
[ 0.36775845, 0.24078108, 0.122042 , 1.1 , 1.1 ],
[-1.48252741, -0.69347186, 1.1 , -0.30606473, 0.41598897],
[ 0.39438905, -1.31770556, 1.1 , -1.52812773, -0.47703227],
[-0.9822216 , -1.09482936, -0.81834523, 1.1 , 1.1 ]]) 4.2 通用判断函数
np.all(布尔值):只有全是True才返回True,只要有一个False就返回False
In[1] :np.all(stock_change[0:2, 0:5] > 0)
Out[1]: Falsenp.any(布尔值):只要有一个True就返回True,只有全是False才返回False
# 判断前5只股票这段期间是否有上涨的
In[1] :np.any(stock_change[:5, :] > 0)
Out[1]: True4.3 np.where(三元运算符)
通过使用np.where(布尔值, True的位置的值, False的位置的值)能够进行更加复杂的运算
# 判断前四个股票前四天的涨跌幅 大于0的置为1,否则为0
temp = stock_change[:4, :4]
# 方法一:
In[1] :temp
Out[1]: array([[ 1.1 , -0.45576704, 0.29667843, 0.16606916],
[ 0.36775845, 0.24078108, 0.122042 , 1.1 ],
[-1.48252741, -0.69347186, 1.1 , -0.30606473],
[ 0.39438905, -1.31770556, 1.1 , -1.52812773]])
In[1] :np.where(temp > 0, 1, 0) # 大于零的位置置为 1,小于零的位置置为 0
Out[1]: array([[1, 0, 1, 1],
[1, 1, 1, 1],
[0, 0, 1, 0],
[1, 0, 1, 0]])
# 方法二:
In[1] :temp > 0
Out[1]: array([[ True, False, True, True],
[ True, True, True, True],
[False, False, True, False],
[ True, False, True, False]])
In[1] :np.where([[ True, False, True, True],
[ True, True, True, True],
[False, False, True, False],
[ True, False, True, False]], 1, 0)
Out[1]: array([[1, 0, 1, 1],
[1, 1, 1, 1],
[0, 0, 1, 0],
[1, 0, 1, 0]])复合逻辑需要结合np.logical_and()和np.logical_or()使用
# 判断前四个股票前四天的涨跌幅 大于0.5并且小于1的,换为1,否则为0
# (temp > 0.5) and (temp < 1) 报错
# 方法一:
In[1] :np.logical_and(temp > 0.5, temp < 1)
Out[1]: array([[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[False, False, False, False]])
In[1] :np.where([[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[False, False, False, False]], 1, 0)
Out[1]: array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])
# 方法二:
In[1] :np.where(np.logical_and(temp > 0.5, temp < 1), 1, 0)
Out[1]: array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])# 判断前四个股票前四天的涨跌幅 大于0.5或者小于-0.5的,换为1,否则为0
# 方法一:
In[1] :np.logical_or(temp > 0.5, temp < -0.5)
Out[1]: array([[ True, False, False, False],
[False, False, False, True],
[ True, True, True, False],
[False, True, True, True]])
# 同上
# 方法二:
In[1] :np.where(np.logical_or(temp > 0.5, temp < -0.5), 11, 3)
Out[1]: array([[11, 3, 3, 3],
[ 3, 3, 3, 11],
[11, 11, 11, 3],
[ 3, 11, 11, 11]])4.4 统计运算
4.4.1 统计指标
np.函数名或者ndarray.方法名:在数据挖掘/机器学习领域, 统计指标的值也是我们分析问题的一种方式。
np.min(a[, axis, out, keepdims])- Return the minimum of an array or minimum along an axis
np.max(a[, axis, out, keepdims])- Return the maximum of an array or maximum along an axis
np.median(a[, axis, out, overwrite_ input, keepdims])- Compute the median along the specified axis
np.mean(a[, axis, dtype, out, keepdims])- Compute the arithmetic mean along the specified axis
np.std(a[, axis, dtype, out, ddof, keepdims])- Compute the standard deviation along the specified axis
np.var(a[, axis, dtype, out, ddof, keepdims])- Compute the variance along the specified axis
4.4.2 股票涨跌幅统计运算
进行统计的时候,axis轴的取值并不一定,Numpy中不同的API轴的值都不一样。在这里,axis=0代表列,axis=1代表行去进行统计。
# 前四只股票前四天的最大涨幅
In[1] :temp # shape: (4, 4) 0 1
Out[1]: array([[ 1.1 , -0.45576704, 0.29667843, 0.16606916],
[ 0.36775845, 0.24078108, 0.122042 , 1.1 ],
[-1.48252741, -0.69347186, 1.1 , -0.30606473],
[ 0.39438905, -1.31770556, 1.1 , -1.52812773]])
# 求所有元素最大值
In[1] :temp.max()
Out[1]: 1.1
# 求各列元素最大值
In[1] :temp.max(axis=0)
Out[1]: array([1.1 , 0.24078108, 1.1 , 1.1 ])
# 求各行元素最大值
In[1] :np.max(temp, axis=-1) # -1 表示最后一个维度
Out[1]: array([1.1, 1.1, 1.1, 1.1])返回最大最小值所在的位置:
np.argmax(temp, axis=)np.argmin(temp, axis=)
# 获取股票指定哪一天的涨幅最大
In[1] :np.argmax(temp, axis=-1)
Out[1]: array([0, 3, 2, 2], dtype=int64)注意:如果多个位置数据相同,返回第一个数据所在位置
5 数组间运算
5.1 数组与数的运算
arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
In[1] :arr / 10
Out[1]: array([[0.1, 0.2, 0.3, 0.2, 0.1, 0.4],
[0.5, 0.6, 0.1, 0.2, 0.3, 0.1]])
# 对比 python列表的运算
a = [1, 2, 3, 4, 5]
In[1] :a * 3
Out[1]: [1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5]5.2 数组与数组的运算(行不通)
arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr2 = np.array([[1, 2, 3, 4], [3, 4, 5, 6]])
In[1] :arr1 # (2, 6)
Out[1]: array([[1, 2, 3, 2, 1, 4],
[5, 6, 1, 2, 3, 1]])
In[1] :arr2 # (2, 4)
Out[1]: array([[1, 2, 3, 4],
[3, 4, 5, 6]])
# arr1 + arr2,报错5.3 广播机制(broadcast)
执行broadcast的前提在于,两个ndarray执行的是element-wise的运算,Broadcast机制的功能是为了方便不同形状的ndarray(numpy库的核心数据结构)进行数学运算。
- 当操作两个数组时,numpy会从右往左逐个比较它们的shape(构成的元组tuple),两个数组运算需要满足下述任意条件:
- 维度相等
- shape(其中相对应的一个地方为1)
- 结果的维度取数组每个shape的最大值
例如:可以运算
Image (3d array):256 × 256 × 3
Scale (1d array): 3
Result(3d array):256 × 256 × 3
A (4d array):9 × 1 × 7 × 1
B (3d array) : 8 × 1 × 5
Result(4d array):9 × 8 × 7 × 5
A (2d array):5 × 4
B (1d array): 1
Result(2d array):5 × 4
A (3d array):15 × 3 × 5
B (3d array):15 × 1 × 1
Result (3d array):15 × 3 × 5示例:
arr1 = np.array([[1, 2, 3, 2, 1, 4],
[5, 6, 1, 2, 3, 1]]) # (2, 6)
arr2 = np.arrayarray([[1],
[3]]) # (2, 2)
In[1] :arr1 + arr2 # (2, 6)
Out[1]: array([[2, 3, 4, 3, 2, 5],
[8, 9, 4, 5, 6, 4]])
In[1] :arr1 * arr2
Out[1]: array([[ 1, 2, 3, 2, 1, 4],
[15, 18, 3, 6, 9, 3]])5.4 矩阵运算
5.4.1 什么是矩阵
矩阵,英文matrix,和array的区别矩阵必须是2维的,但是array可以是多维的。
矩阵与二维数组区别:矩阵一定是二维数组,二维数组不一定是矩阵。
两种方法存储矩阵:
- ndarray 二维数组
- matrix数据结构
np.mat():将数组(ndarray 二维数组)转换成矩阵类型
# 方法一:
# ndarray存储矩阵
data = np.array([[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]])
# 方法二:
# matrix存储矩阵:
In[1] :np.mat(data)
Out[1]: matrix([[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]])
In[1] :type(np.mat(data))
Out[1]: numpy.matrix5.4.2 矩阵乘法运算
矩阵乘法: ( M 行 , N 列 ) × ( N 行 , L 列 ) = ( M 行 , L 列 ) (M行, N列)×(N行, L列)=(M行, L列) (M行,N列)×(N行,L列)=(M行,L列)
ndarray二维数组矩阵乘法API:np.matmul(),np.dot()
1. ndarray矩阵运算:
In[1] :data # (8, 2) * (2, 1) = (8, 1)
Out[1]: array([[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]])
weights = np.array([[0.3], [0.7]])
In[1] :weights
Out[1]: array([[0.3],
[0.7]])
# 方法一:
In[1] :np.matmul(data, weights)
Out[1]: array([[84.2],
[80.6],
[80.1],
[90. ],
[83.2],
[87.6],
[79.4],
[93.4]])
# 方法二:
In[1] :np.dot(data, weights)
Out[1]: array([[84.2],
[80.6],
[80.1],
[90. ],
[83.2],
[87.6],
[79.4],
[93.4]])注意: data * weights 不满足广播机制,不能进行运算。
2. matrix数据结构矩阵运算
data_mat = np.mat(data)
weights_mat = np.mat([[0.3], [0.7]])
In[1] :weights_mat
Out[1]: matrix([[0.3],
[0.7]])
In[1] :data_mat * weights_mat
Out[1]: matrix([[84.2],
[80.6],
[80.1],
[90. ],
[83.2],
[87.6],
[79.4],
[93.4]])3. ndarray矩阵运算直接相乘:@
In[1] :data @ weights
Out[1]: array([[84.2],
[80.6],
[80.1],
[90. ],
[83.2],
[87.6],
[79.4],
[93.4]])6 合并与分割
将数据进行切分合并处理。
6.1 合并
numpy.hstack(tup):Stack arrays in sequence horizontally(column wise).numpy.vstack(tup):Stack arrays in sequence vertically(row wise).numpy.concatenate((a1, a2, ...), axis=0)
data1= np.array([[1, 2],[3, 4],[5, 6]]) # (2, 3)
In[1] :data1
Out[1]: array([[1, 2],
[3, 4],
[5, 6]])
data2 = np.array([[7, 8],[9, 10],[11, 12]])
In[1] :data2
Out[1]: array([[ 7, 8],
[ 9, 10],
[11, 12]])
# 列拼接
In[1] :np.hstack((data1, data2))
Out[1]: array([[ 1, 2, 7, 8],
[ 3, 4, 9, 10],
[ 5, 6, 11, 12]])
# axis=1时候,按照数组的列方向拼接在一起
In[1] :np.concatenate((data1, data2), axis = 1)
Out[1]: array([[ 1, 2, 7, 8],
[ 3, 4, 9, 10],
[ 5, 6, 11, 12]])
# 行拼接
In[1] :np.vstack((data1, data2))
Out[1]: array([[ 1, 2],
[ 3, 4],
[ 5, 6],
[ 7, 8],
[ 9, 10],
[11, 12]])
# axs=0时候,按照数组的行方向拼接在一起
In[1] :np.concatenate((data1, data2), axis = 0)
Out[1]: array([[ 1, 2],
[ 3, 4],
[ 5, 6],
[ 7, 8],
[ 9, 10],
[11, 12]])6.2 分割
numpy.split(ary, indices_or_sections, axis=0):Split an array into multiple sub-arrays.
x = np.arange(9.0)
# 按组数划分,平均分为三组
In[1] :x
Out[1]: array([0., 1., 2., 3., 4., 5., 6., 7, 8.])
In[1] :np.split(x,3)
Out[1]: [array([0., 1., 2.]), array([3., 4., 5.]), array([6., 7., 8.])]
# 按索引分割,四组,第一组:[0,3),第二组:[3,5),第三组:[5,6),第四组:[6,...)
In[1] :np.split(x,[3, 5, 6])
Out[1]: [array([0., 1., 2.]),
array([3., 4.]),
array([5.]),
array([6., 7., 8.])]7 IO操作与数据处理(常用pandas)
问题:大多数数据是存在文件当中,需要用工具获取。
Numpy并不适合读取和处理数据,本节仅做简单了解。
7.1 Numpy读取
genfromtxt(fname[, dtype, comments, delimiter, ...):Load data from a text file, with missing values handled as specified.- fname:文件路径
- delimiter:分隔符
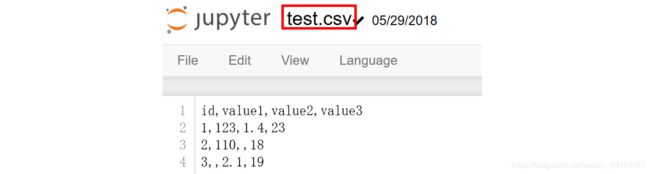
data = np.genfromtxt("test.csv", delimiter=",")
In[1] :data
Out[1]: array([[ nan, nan, nan, nan],
[ 1. , 123. , 1.4, 23. ],
[ 2. , 110. , nan, 18. ],
[ 3. , nan, 2.1, 19. ]])缺点: numpy将字符串读取为缺失值(nan)
7.2 缺失值处理
缺失值:当读取本地的文件为float时,如果有缺失(或者为None),就会岀现nan。
如果nan全部替换为0后,替换之前的平均值如果大于0,替换之后的均值会变小。
处理缺失值两种思路:
- 直接删除含有缺失值的样本
- 替换/插补:按列求平均,用平均值进行填补
如何计算一组数据的中值或者是均值,以及删除有缺失数据的那一行(列)在
pandas中介绍。
查看 nan 类型:
In[1] :type(data[2, 2])
Out[1]: numpy.float64 # 浮点型处理 nan(不建议):
def fill_nan_by_column_mean(t):
# 遍历列
for i in range(t.shape[1]):
# 计算nan的个数
nan_num = np.count_nonzero(t[:, i][t[:, i] != t[:, i]])
if nan_num > 0:
now_col = t[:, i]
# 求和
now_col_not_nan = now_col[np.isnan(now_col) == False].sum()
# 和/个数
now_col_mean = now_col_not_nan / (t.shape[0] - nan_num)
# 赋值给now_col
now_col[np.isnan(now_col)] = now_col_mean
# 赋值给t,即更新t的当前列
t[:, i] = now_col
return tIn[1] :data
Out[1]: array([[ nan, nan, nan, nan],
[ 1. , 123. , 1.4, 23. ],
[ 2. , 110. , nan, 18. ],
[ 3. , nan, 2.1, 19. ]])
In[1] :fill_nan_by_column_mean(data)
Out[1]: array([[ 2. , 116.5 , 1.75, 20. ],
[ 1. , 123. , 1.4 , 23. ],
[ 2. , 110. , 1.75, 18. ],
[ 3. , 116.5 , 2.1 , 19. ]])