基于机器学习的回归拟合、详细总结

有导师学习神经网络的回归拟合

    神经网络的学习规则又称神经网络的训练算法,用来计算更新神经网络的权值和阈值。
学习规则有两大类别;有导师学习和无导师学习。在有导师学习中,需要为学习规则提供一系
列正确的网络输入/输出对(即训练样本)，当网络输人时,将网络输出与相对应的期望值进行
比较﹐然后应用学习规则调整权值和阈值，使网络的输出接近于期望值。而在无导师学习中，
权值和阈值的调整只与网络输人有关系，没有期望值﹐这类算法大多用聚类法,将输人模式归
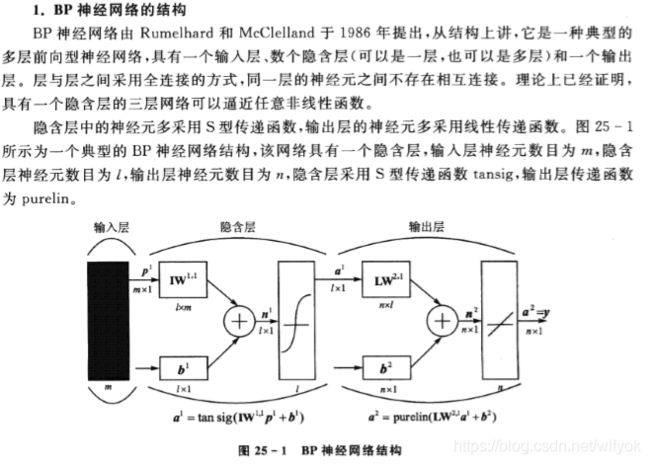
类于有限的类别。本章将详细分析两种应用最广的有导师学习神经网络(BP神经网络及
RBF神经网络)的原理及其在回归拟合中的应用。

BP神经网络

题目与思路

辛烷值是汽油最重要的品质指标,传统的实验室检测方法存在样品用量大.测试周期长和费用高等问题，不适用于生产控制﹐特别是在线测试。近年发展起来的近红外光谐分析方法(NIR)，作为一种快速分析方法,已广泛应用于农业.制药、生物化工.石油产品等领域。其优越性是无损检测﹑低成本、无污染、能在线分析，更适合于生产和控制的需要。针对采集得到的60组汽油样品﹐利用傅里叶近红外变换光谱仪对其进行扫描，扫描范围为900~1 700 nm,扫描间隔为2 nm,每个样品的光谱曲线共含401个波长点。样品的近红外光谐曲线如图25-3所示。同时﹐利用传统实验室检测方法测定其辛烷值含量。现要25-360个样品的近红外光谱圉求利用BP神经网络及RBF神经网络分别建立汽油样品近红外光谱及其辛烷值间的数学模型,并对模型的性能进行评价。

代码与结果

详细代码私聊笔者，有偿，非诚勿扰

% 基于近红外光谱的汽油辛烷值预测
clear
clc
% 产生训练集/测试集
load spectra_data.mat
temp  = randperm(size(NIR,1));
ptrain = NIR(temp(1:50),:)';
ttrain = octane(temp(1:50),:)';
ptest = NIR(temp(51:end),:)';
ttest = octane(temp(51:end),:)';
n = size(ptest,2);
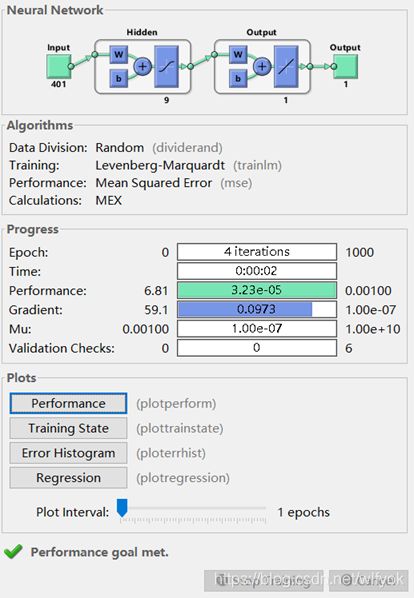
% 创建/训练BP神经网络及仿真测试
net = feedforwardnet(9);
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
net.trainParam.lr = 0.01;
net = train(net,ptrain,ttrain);
tsimbp = net(ptest);
net = newrbe(ptrain,ttrain,0.5);
tsimrbf = sim(net,ptest);
% 性能评价
errorbp = abs(tsimbp-ttest)./ttest;
errorrbf = abs(tsimrbf-ttest)./ttest;
r2bp = (n*sum(tsimbp.*ttest)-sum(tsimbp)*sum(ttest))^2/((n*sum((tsimbp).^2)-(sum(tsimbp))^2)*(n*sum((ttest).^2)-(sum(ttest))^2));
r2rbf = (n*sum(tsimrbf.*ttest)-sum(tsimrbf)*sum(ttest))^2/((n*sum((tsimrbf).^2)-(sum(tsimrbf))^2)*(n*sum((ttest).^2)-(sum(ttest))^2));
result = [ttest' tsimbp' tsimrbf' errorbp' errorrbf'];
% 绘图
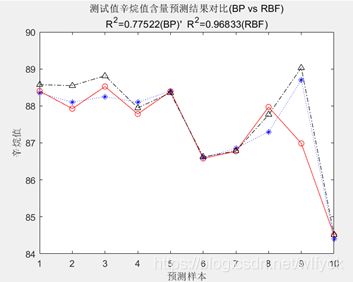
figure
plot(1:n,ttest,'b:*',1:n,tsimbp,'r-o',1:n,tsimrbf,'k-.^')
legend('真实值','BP预测值','RBF预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {
     '测试值辛烷值含量预测结果对比(BP vs RBF)';['R^2=',num2str(r2bp),'(BP)''  R^2=',num2str(r2rbf),'(RBF)']};
title(string)

详细代码私聊笔者，有偿，非诚勿扰

支持向量机的回归拟合

与传统的神经网络相比，SVM具有以下几个优点：
（1）SVM是专门针对小样本问题而提出的，其可以在有限样本的情况下获得最优解；
（2）SVM算法最终将转化为一个二次规划问题，从理论上讲可以得到全局最优解，从而解决了传统神经网无法避免局部最优的问题；
（3）SVM的拓扑结构由支持向量决定，避免了传统神经网络需要反复试凑确定网络结构的问题；
（4）SVM利用非线性变换将原始变量映射到高维特征空间，在高维特征空间中构造线性分类函数，这既保证了模型具有良好的泛化能力，又解决了“维数灾难”问题。
同时，SVM不仅可以解决分类、模式识别等问题，还可以解决回归、拟合等问题。因此，其在各个领域中都得到了非常广泛的利用。
本章将详细介绍SVM回归拟合的基本思想和原理，并以实例的形式阐述其在混凝土抗压强度预测中的应用。
随着技术的不断发展，混凝土抗压强度检测手段也愈来愈多，基本上可以分为局部破损法和非破损法两类，其中局部破损法主要是钻芯法，非破损法主要包括回弹法和超声法。工程上常采用钻芯法修正回弹法并结合《回弹法检测混凝土抗压强度技术规程》、《建筑结构检测技术标准》等规定的方法来推定混凝土的抗压强度。按照传统的方法，通常需要先对混凝土试件进行28天标准养护，然后通过测试获得。若能够提前预测出混凝土的28天抗压强度，则对于提高施工的质量和进度都具有重要的参考意义和实用价值。
此外，不少专家和学者将投影寻踪回归、神经网络、灰色理论等方法引入到混凝土结构工程领域中，取得了不错的效果，对混凝土抗压强度的预测有着一定的指导意义。
相关研究成果表明，混凝土的28天立方米抗压强度与混凝土的组成有很大的关系，即与每立方米混凝土中水泥、炉石、飞灰、水、超增塑剂、碎石及砂用量的多少有显著的关系。

SVR基本思想

问题描述与算法流程

现采集到103组混凝土样本的立方米抗压强度及其中上述7种成分的含量大小，要求利用支持向量机建立混凝土的28天立方米抗压强度与其组成间的回归数学模型，并对模型的性能进行评价。

代码及结果`

详细代码私聊笔者，有偿，非诚勿扰

% 混凝土抗压实验预测
clear
clc
% 产生训练集/测试集
load concrete_data.mat
n = randperm(size(attributes,2));
ptrain = attributes(:,n(1:80))';
ttrain = strength(:,n(1:80))';
ptest = attributes(:,n(81:end))';
ttest = strength(:,n(81:end))';
% 数据归一化
[pntrain,inputs] = mapminmax(ptrain');
pntrain = pntrain';
pntest = mapminmax('apply',ptest',inputs);
pntest = pntest';
[tntrain,outputs] = mapminmax(ttrain');
tntrain = tntrain';
tntest = mapminmax('apply',ttest',outputs);
tntest = tntest';
% 创建/训练SVR模型
[c,g] = meshgrid(-10:0.5:10,-10:0.5:10);
[m,n] = size(c);
cg = zeros(m,n);
eps = 1e-4;
v = 5;
bestc = 0;
bestg = 0;
error = inf;
for i = 1:m
    for j = 1:n
        cmd = ['-v ',num2str(v),' -c ',num2str(2^c(i,j)),' -g',num2str(2^g(i,j) ),' -s 3 -p 0.1'];
        cg(i,j) = svmtrain(tntrain,pntrain,cmd);
        if cg(i,j) < error
            error = cg(i,j);
            bestc = 2^c(i,j);
            bestg = 2^g(i,j);
        end
        if abs(cg(i,j) - error) <= eps && bestc > 2^c(i,j)
            error = cg(i,j);
            bestc = 2^c(i,j);
            bestg = 2^g(i,j);
        end
    end
end
cmd = ['-c ',num2str(bestc),' -g ',num2str(bestg),' -s 3 -p 0.01'];
model = svmtrain(tntrain,pntrain,cmd);
% SVR仿真
[predict1,error1] = svmpredict(tntrain,pntrain,model);
[predict2,error2] = svmpredict(tntest,pntest,model);
predict1 = mapminmax('reverse',predict1,outputs);
predict2 = mapminmax('reverse',predict2,outputs);
result1 = [ttrain predict1];
result2 = [ttest predict2];
% 绘图
figure(1)
plot(1:length(ttrain),ttrain,'r-*',1:length(ttrain),predict1,'b:o')
grid on
legend('真实值','预测值')
xlael('样本编号')
ylabel('耐压强度')
string1 = {
     '训练集预测结果对比';['mse=',num2str(error1(2)),'R^2=',num2str(error1(3))]};
title(string1)
figure(2)
plot(1:length(ttest),ttest,'r-*',1:length(ttest),predict2,'b:o')
grid on
legend('真实值','预测值')
xlael('样本编号')
ylabel('耐压强度')
string1 = {
     '训练集预测结果对比';['mse=',num2str(error2(2)),'R^2=',num2str(error2(3))]};
title(string2)

详细代码私聊笔者，有偿，非诚勿扰