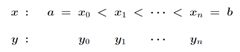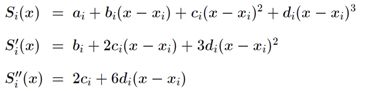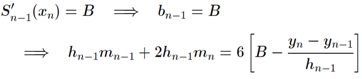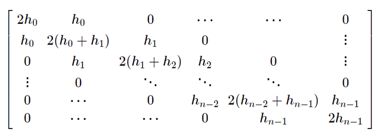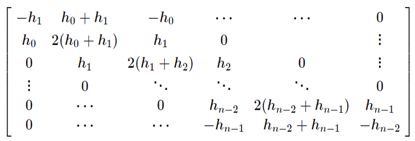三次样条插值(Cubic Spline Interpolation)及代码实现(C语言)

样条插值是一种工业设计中常用的、得到平滑曲线的一种插值方法，三次样条又是其中用的较为广泛的一种。本篇介绍力求用容易理解的方式，介绍一下三次样条插值的原理，并附C语言的实现代码。

1. 三次样条曲线原理

假设有以下节点

 

 

1.1 定义

样条曲线 是一个分段定义的公式。给定n+1个数据点，共有n个区间，三次样条方程满足以下条件：

a. 在每个分段区间 （i = 0, 1, …, n-1，x递增），  都是一个三次多项式。

b. 满足 （i = 0, 1, …, n ）

c.  ，导数 ，二阶导数 在[a, b]区间都是连续的，即曲线是光滑的。

所以n个三次多项式分段可以写作：

 ，i = 0, 1, …, n-1

其中ai, bi, ci, di代表4n个未知系数。

1.2 求解

已知:

a. n+1个数据点[xi, yi], i = 0, 1, …, n

b. 每一分段都是三次多项式函数曲线

c. 节点达到二阶连续

d. 左右两端点处特性（自然边界，固定边界，非节点边界）

根据定点，求出每段样条曲线方程中的系数，即可得到每段曲线的具体表达式。

 

插值和连续性：

, 其中 i = 0, 1, …, n-1

微分连续性：

 , 其中 i = 0, 1, …, n-2

样条曲线的微分式：

 

将步长 带入样条曲线的条件：

a. 由 (i = 0, 1, …, n-1)推出

b. 由 (i = 0, 1, …, n-1)推出

c. 由  (i = 0, 1, …, n-2)推出

由此可得：

d. 由  (i = 0, 1, …, n-2)推出

 

设 ，则

a.  可写为：

 ，推出

b. 将ci, di带入  可得：

c. 将bi, ci, di带入 (i = 0, 1, …, n-2)可得：

端点条件

由i的取值范围可知，共有n-1个公式， 但却有n+1个未知量m 。要想求解该方程组，还需另外两个式子。所以需要对两端点x0和xn的微分加些限制。 选择不是唯一的，3种比较常用的限制如下。

a. 自由边界(Natural)

首尾两端没有受到任何让它们弯曲的力，即 。具体表示为 和 

则要求解的方程组可写为：

 

 

b. 固定边界(Clamped)

首尾两端点的微分值是被指定的，这里分别定为A和B。则可以推出

将上述两个公式带入方程组，新的方程组左侧为

c. 非节点边界(Not-A-Knot)

指定样条曲线的三次微分匹配，即

根据 和 ，则上述条件变为

新的方程组系数矩阵可写为：

 

 

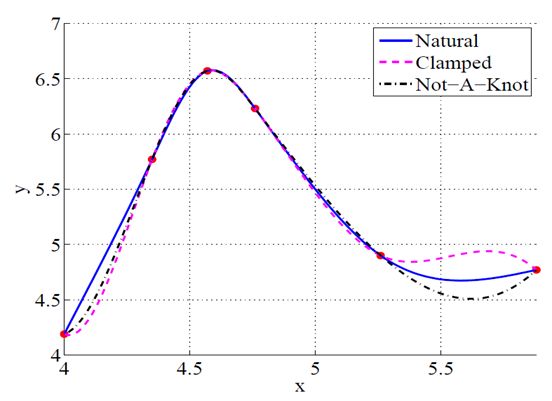
右下图可以看出不同的端点边界对样条曲线的影响：

 

1.3 算法总结

假定有n+1个数据节点

a. 计算步长 (i = 0, 1, …, n-1)

b. 将数据节点和指定的首位端点条件带入矩阵方程

c. 解矩阵方程，求得二次微分值。该矩阵为三对角矩阵，具体求法参见我的上篇文章：三对角矩阵的求解。

d. 计算样条曲线的系数：

其中i = 0, 1, …, n-1

e. 在每个子区间 中，创建方程

 

2. C语言实现

用C语言写了一个三次样条插值(自然边界)的S-Function，代码如下：

#define S_FUNCTION_NAME  cubic
#define S_FUNCTION_LEVEL 2
#include "simstruc.h"
#include "malloc.h"  //方便使用变量定义数组大小

static void mdlInitializeSizes(SimStruct *S)
{
    /*参数只有一个，是n乘2的定点数组[xi, yi]:
     * [ x1，y1;
     *   x2, y2;
     *   ..., ...;
     *   xn, yn;
    */
    ssSetNumSFcnParams(S, 1); 
    if (ssGetNumSFcnParams(S) != ssGetSFcnParamsCount(S)) return;

    ssSetNumContStates(S, 0);
    ssSetNumDiscStates(S, 0);

    if (!ssSetNumInputPorts(S, 1)) return;  //输入是x
    ssSetInputPortWidth(S, 0, 1);
    ssSetInputPortRequiredContiguous(S, 0, true);
    ssSetInputPortDirectFeedThrough(S, 0, 1);

    if (!ssSetNumOutputPorts(S, 1)) return;  //输出是S(x)
    ssSetOutputPortWidth(S, 0, 1);

    ssSetNumSampleTimes(S, 1);
    ssSetNumRWork(S, 0);
    ssSetNumIWork(S, 0);
    ssSetNumPWork(S, 0);
    ssSetNumModes(S, 0);
    ssSetNumNonsampledZCs(S, 0);

    ssSetSimStateCompliance(S, USE_DEFAULT_SIM_STATE);

    ssSetOptions(S, 0);
}

static void mdlInitializeSampleTimes(SimStruct *S)
{
    ssSetSampleTime(S, 0, CONTINUOUS_SAMPLE_TIME);
    ssSetOffsetTime(S, 0, 0.0);
}



#define MDL_INITIALIZE_CONDITIONS
#if defined(MDL_INITIALIZE_CONDITIONS)
  static void mdlInitializeConditions(SimStruct *S)
  {
  }
#endif



#define MDL_START
#if defined(MDL_START) 
  static void mdlStart(SimStruct *S)
  {
  }
#endif /*  MDL_START */


static void mdlOutputs(SimStruct *S, int_T tid)
{
    const real_T *map = mxGetPr(ssGetSFcnParam(S,0));  //获取定点数据
    const int_T *mapSize = mxGetDimensions(ssGetSFcnParam(S,0));  //定点数组维数
    const real_T *x = (const real_T*) ssGetInputPortSignal(S,0);  //输入x
    real_T       *y = ssGetOutputPortSignal(S,0); //输出y
    int_T step = 0;  //输入x在定点数中的位置
    int_T i;
    real_T yval;

    for (i = 0; i < mapSize[0]; i++)
    {
        if (x[0] >= map[i] && x[0] < map[i + 1])
        {
            step = i;
            break;
        }
    }
    
    cubic_getval(&yval, mapSize, map, x[0], step);
    y[0] = yval;
    
}

//自然边界的三次样条曲线函数
void cubic_getval(real_T* y, const int_T* size, const real_T* map, const real_T x, const int_T step)
{
    int_T n = size[0];
    
    //曲线系数
    real_T* ai = (real_T*)malloc(sizeof(real_T) * (n-1));
    real_T* bi = (real_T*)malloc(sizeof(real_T) * (n-1));
    real_T* ci = (real_T*)malloc(sizeof(real_T) * (n-1));
    real_T* di = (real_T*)malloc(sizeof(real_T) * (n-1));
    
    real_T* h = (real_T*)malloc(sizeof(real_T) * (n-1));  //x的??
    
    /* M矩阵的系数
     *[B0, C0, ...
     *[A1, B1, C1, ...
     *[0,  A2, B2, C2, ...
     *[0, ...             An-1, Bn-1]
     */
    real_T* A = (real_T*)malloc(sizeof(real_T) * (n-2));
    real_T* B = (real_T*)malloc(sizeof(real_T) * (n-2));
    real_T* C = (real_T*)malloc(sizeof(real_T) * (n-2));
    real_T* D = (real_T*)malloc(sizeof(real_T) * (n-2)); //等号右边的常数矩阵
    real_T* E = (real_T*)malloc(sizeof(real_T) * (n-2)); //M矩阵
    
    real_T* M = (real_T*)malloc(sizeof(real_T) * (n));  //包含端点的M矩阵
    
    int_T i;
    
    //计算x的步长
    for ( i = 0; i < n -1; i++)
    {
        h[i] = map[i + 1] - map[i];
    }
    
    //指定系数
    for( i = 0; i< n - 3; i++)
    {
        A[i] = h[i]; //忽略A[0]
        B[i] = 2 * (h[i] + h[i+1]);
        C[i] = h[i+1]; //忽略C(n-1)
    }

    
    //指定常数D
    for (i = 0; i=0; i--)
    {
        X[i] = D[i] - C[i] * X[i+1];
    }
}


#define MDL_UPDATE 
#if defined(MDL_UPDATE)
  static void mdlUpdate(SimStruct *S, int_T tid)
  {
  }
#endif

#define MDL_DERIVATIVES
#if defined(MDL_DERIVATIVES)
  static void mdlDerivatives(SimStruct *S)
  {
  }
#endif

static void mdlTerminate(SimStruct *S)
{
}

#ifdef  MATLAB_MEX_FILE  
#include "simulink.c"
#else
#include "cg_sfun.h"
#endif

 

3. 例子

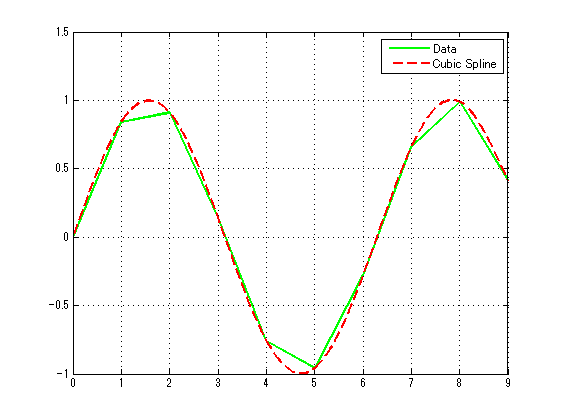
以y=sin(x)为例,  x步长为1，x取值范围是[0,9]。对它使用三次样条插值，插值前后对比如下：