Python探索性数据分析——异常数据的检测与处理、数据的描述（集中、分散、分布、相关关系、波动）、数据的推断（正态性检验、卡方检验、t检验）

前言：
在数据读取、处理之后就需要进一步地进行数据分析了，在这其中首先进行的就是常规的探索性数据分析。这个过程将涉及数据的检查（如缺失值、重复值、异常值）、数据的描述（如集中趋势、分散趋势、分布形状、相关关系等）以及数据的推断（如假设检验、模型的构建、特征选择等）。
本文主要介绍有关探索性数据分析过程中的数据检查和数据描述的常用技术。在数据的探索过程中，经常会用到数据可视化技术，例如通过折现趋势图可以发现数据的波动特征；利用散点图可以挖掘数据内在的数学关系；采用直方图则可以发现数据的集中区间和分布形态等。
前置数据处理技术参见：Python常见数据处理技术——数据的概览与清洗、多表合并与连接、数据的汇总
后置数据处理技术参见：Python——线性回归模型的应用

由于针对具体操作相关文档太多，所以本文内容涉及具体操作较少，主要是讲方法。

本文内所用到的包：

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import scipy.stats as stats
import statsmodels.api as sm
from scipy.stats import chi2_contingency

一.异常数据的检测与处理

对于异常值处理办法：

1. 直接从数据集中删除异常点
2. 使用简单数值（均值或中位数）或者距离异常值最近的最大值（最小值）替换异常值，也可以使用判断异常值的临界值替换异常值
3. 将异常值当做缺失值处理，使用插补法估计异常值，或者根据异常值衍生出表示是否异常的哑变量（参见：Python——线性回归模型的应用）

1.异常数据检测与处理-基于箱线图

建议该方法在待判断变量不服从于正态分布时使用

以经典的太阳黑子为例：

sunspots=pd.read_csv('sunspots.csv',sep=',')

绘制箱线图（1.5倍的四分位差，如需绘制3倍的四分位差，只需调整whis参数）

plt.boxplot(x=sunspots.counts,#指定绘制箱图的数据
                whis=1.5,#指定1.5倍的四分位差
                widths=0.7,#指定箱线图的宽度为0.7
                patch_artist=True,#指定需要填充箱体的颜色
                showmeans=True,#指定需要显示均值
                boxprops={
     'facecolor':'steelblue'},#指定箱体的填充色为铁蓝色
                flierprops={
     'markerfacecolor':'red','markeredgecolor':'red','markersize':4},#指定异常点的填充色，边框色和大小
                meanprops={
     'marker':'D','markerfacecolor':'black','markersize':4},#指定均值点的标记符号（菱形）、填充色和大小
                medianprops={
     'linestyle':'--','color':'orange'},#指定中位数的标记符号（虚线）和颜色
                labels=['']#去掉箱线图的X轴刻度值
                )

由图可知数据存在异常值，接下来去找出这些异常值

#计算下四分位数和上四分位
Q1=sunspots.counts.quantile(q=0.25)
Q3=sunspots.counts.quantile(q=0.75)
#基于1.5倍的四分卫差计算上下须对应的值
low_whisker = Q1-1.5*(Q3-Q1)
up_whisker = Q3+1.5*(Q3-Q1)
#寻找异常点
exploring = sunspots.counts[(sunspots.counts>up_whisker)|(sunspots.counts<low_whisker)]

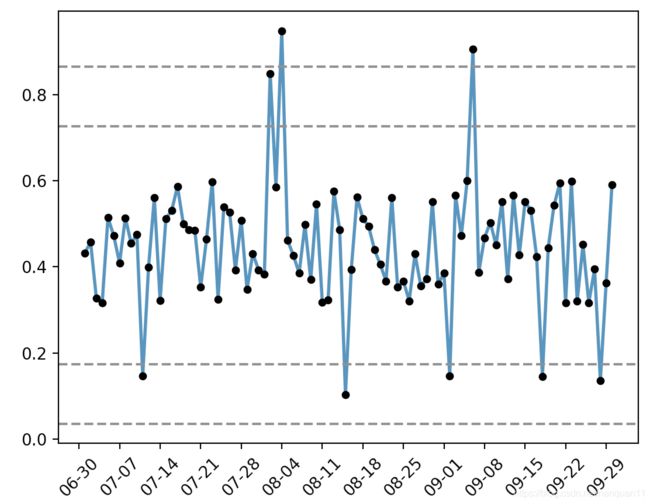
2.异常数据检测与处理-基于正态分布特征

待判断变量近似服从于正态分布时使用

• 如果数据点落在偏离均值正负2倍标准差之外，属于小概率事件——异常点
• 如果数据点落在偏离均值正负3倍标准差之外，属于更小概率事件——极端异常点

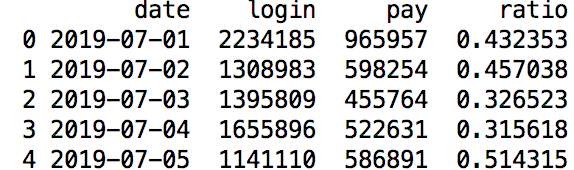
以经典的公司支付转化率为例：

pay_ratio=pd.read_excel('pay_ratio.xlsx')

绘制单条折线图，并在折线图的基础上添加点图

plt.plot(pay_ratio.date,#X轴数据
             pay_ratio.ratio,#Y轴数据
             linestyle='-',#设置折线类型
             linewidth=2,#设置线条宽度
             color='steelblue',#设置折线颜色
             marker='o',#往折线图中添加圆点
             markersize=4,#设置点的大小
             markeredgecolor='black',#设置点的边框色
             markerfacecolor='black'#设置点的填充色
             )

添加上下界的水平参考线（便于判断异常点，如下面判断极端异常点，只需将2改为3）

plt.axhline(y=pay_ratio.ratio.mean()-2*pay_ratio.ratio.std(),linestyle='--',color='gray')
plt.axhline(y=pay_ratio.ratio.mean()+2*pay_ratio.ratio.std(),linestyle='--',color='gray')
plt.axhline(y=pay_ratio.ratio.mean()-3*pay_ratio.ratio.std(),linestyle='--',color='gray')
plt.axhline(y=pay_ratio.ratio.mean()+3*pay_ratio.ratio.std(),linestyle='--',color='gray')

导入模块，用于日期刻度的修改（因为默认格式下的日期刻度标签并不是很友好）

import matplotlib as mpl
#获取图的坐标信息
ax=plt.gca()
#设置日期格式
date_format=mpl.dates.DateFormatter('%m-%d')
ax.xaxis.set_major_formatter(date_format)
#设置X轴每个刻度的间隔天数
xlocator=mpl.ticker.MultipleLocator(7)
ax.xaxis.set_major_locator(xlocator)
plt.xticks(rotation=45)

由图可知数据存在异常值和极端异常值，接下来去找出这些异常值

#计算判断异常点和极端异常点的临界值
outlier_ll = pay_ratio.ratio.mean()-2*pay_ratio.ratio.std()
outlier_ul = pay_ratio.ratio.mean()+2*pay_ratio.ratio.std()
extreme_outlier_ll = pay_ratio.ratio.mean()-3*pay_ratio.ratio.std()
extreme_outlier_ul = pay_ratio.ratio.mean()+3*pay_ratio.ratio.std()
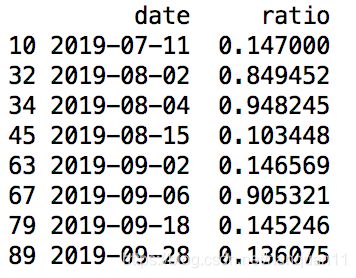
#寻找异常点
result1=pay_ratio.loc[(pay_ratio.ratio>outlier_ul)|(pay_ratio.ratio<outlier_ll),['date','ratio']]
#寻找极端异常点
result2=pay_ratio.loc[(pay_ratio.ratio>extreme_outlier_ul)|(pay_ratio.ratio<extreme_outlier_ll),['date','ratio']]

异常值：
极端异常值：

二.数据的描述

数据的描述过程侧重于统计运算和统计绘图。

• 通过统计运算可以得到具体的数据特征，如反映集中趋势中的均值水平、中位数、分位数和众数等；反映分散趋势的方差、极差、四分位差和变异系数等
• 通过统计绘图可以得到直观的数据规律和知识，如利用直方图发现数据的分布形态、利用散点图得出变量之间的相关关系以及利用折线图呈现数据再时间维度上的波动趋势等。

1.数据的集中趋势

数据的集中趋势也称为中心趋势，反应的是数据的中心代表值

1.1.数据的集中趋势-平均值

1.1.1.算数平均值

使用mean方法

• 优点在于简单易用，不易受抽样的影响（即在同一整体中，不同组的样本其平均水平差异并不大）
• 缺点是容易受到极端值的影响（即可能被数据集中的某个极大值或极小值拉高或压低）

当样本量比较小，且数据的分布呈现偏态特征时，不宜选择算数平均值作为数据的代表值，当样本量非常大时，可以不考虑数据的分布特征，适合用算数平均值

1.1.2.加权平均值

相对于算数平均值而言，因为在算数平均值中设定每个样本的权重均为1，然而在实际的应用中，有时样本的权重并不相等

• 优点是弥补了算数平均值中等权重的缺点，同时一定程度上也避免了极端值的影响
• 缺点是权重的确定容易受到人们主观意识的影响

以经典的RFM为例：

RFM=pd.read_excel('RFM.xlsx')

计算每个用户在R、F、M3个指标上的加权平均得分

RFM['Weight_Mean']=0.2*RFM['R_score']+0.5*RFM['F_score']+0.3*RFM['M_score']

1.1.3.几何平均值

无论是算数平均值还是加权平均值，它们在计算绝对数量的平均水平时时不错的选择，如果数据是相对的比例值时，应该选择几何平均值

以经典的GDP为例：

GDP=pd.read_excel('G_D_P.xlsx')

计算这些年中GDP的平均增长率。对于几何平均值的计算，需要使用序列的cumprod函数及幂指数函数pow

#利用cumprod方法实现所有元素的累计乘积
cum_prod=GDP.Grouth.cumprod()
#基于cum_prod结果，利用索引将最后一个累积元素取出来
res=cum_prod[GDP.shape[0]-1]
#计算几何平均值
result=pow(res,1/len(cum_prod))
print(result)#0.08776443979162651

结果显示，基于几何平均值得出的2007-2016年的10年间的GDP平均增长率约8.78%，但如果使用算数平均数计算的话GDP的平均增长率为9%，所以，在计算比例数据的平均值时，用几何平均值作为其中心的代表最为合适。

1.2.数据的集中趋势-中位数和四分位数

1.2.1.中位数

• 中位数也是特别常用的中心代表值，反映了数据的中心位置（即50%分位点），故可以解决算数平均值易受极端值影响的弊端
• 所以在寻找数据的中心代表值之前，可以先探索数据的分布特征
• 如果存在严重的偏态，则选择中位数会更加合理，否则应选择算数平均数
• 优点在于含义直观（根据数据位置确定该值）、简单易用、不会受到极端值的影响
• 缺点在于计算前需要对数据排序，数据量大时，在一定程度上会影响计算的速度
• 基于matplotlib包的hist函数绘制直方图，根据直方图呈现的分布特征进行选择合适的方法
• 对于中位数的计算，可以使用序列的medain函数

以经典的tips数据为例：

tips=pd.read_csv('tips.csv',sep=',')

tips.tip.hist(grid=False,#去除图框内的网格线
                  facecolor='steelblue',#直方图的填充色为铁蓝色
                  edgecolor='black'#直方图的边框色为黑色
                  )

• 绝大多数小费金额在2~4美元，小费金额数据存在明显的右偏特征
• 应该优先选择中位数作为数据集中趋势的代表

计算小费数据的中位数

print('中位数为：',tips.tip.median())#中位数为： 2.9

计算小消费数据的均值

print('均值为：',tips.tip.mean())#均值为： 2.99827868852459

均值大于中位数，这是因为均值受到了右偏的影响

1.2.2.四分位数

通常借助于中位数和四分卫数可以得到数据的大致分布特征

计算小费数据的上下四分位数

print('下四分位数为：',tips.tip.quantile(q=0.25))#下四分位数为： 2.0
print('上四分位数为：',tips.tip.quantile(q=0.75))#上四分位数为： 3.5624999999999996

消费数据下四分位数位2.0，上四分位为3.563，进而可以大致得到数据的特征：25%的顾客所支付的小费不超过2美元；一半的顾客（中位数）所支付的小费不超过2.9美元；3/4的顾客所支付的小费则不超过3.563美元。

1.3.数据的集中趋势-众数

• 平均值或中位数都是数值型变量的中心代表值，如果数据为离散型变量时，就应该选择众数来衡量其集中趋势
• 众数指变量中出现频次最高的值，如果最高频次对应了多个值，则这些值都成为众数（或复众数）
• 众数也可以体现数值型变量的集中趋势，所不同的是，需要对数值型变量做分组变换
• 优点是可以弥补平均值或中位数的缺陷，因为它们无法衡量离散型和分组性数据的集中趋势，同时避免极端值的影响
• 缺点是对于连续的数值型变量，在计算众数之前需要将数值进行分组

以经典的泰坦尼克号数据为例：

titanic=pd.read_excel('Titanic.xlsx')

计算登船地址的众数

print('登船地址的众数：',titanic.Embarked.mode())

对于基于众数的计算公式，计算出分组变量的中心代表值，以用户收入为例：

income=pd.read_excel('Income.xlsx')

计算众数：

index = income.Counts.argmax()#返回众数所在组的行索引
L=int(income.Income[index].split(',')[0][1:])#返回众数所在组的下限
U=int(income.Income[index].split(',')[1][:-1])#返回众数所在组的上限
#返回左邻与右邻组所对应的频次
LF=income.Counts[index-1]
RF=income.Counts[index+1]
#计算众数
mode = L+LF/(LF+RF)*(U-L)

2.数据的分散趋势

数据的分散趋势是用来刻画数值型变量偏离中心的程度

• 最为常用的分散趋势指标有标准差、极差、四分位差等
• 指标值越大，说明样本之间差异约明显，反之差异越小

2.1.数据的分散趋势-方差与标准差

标准差是方差的二次方根。
该方法在对比多组样本之间的分散程度时不合适（例如两组样本之间的样本量相差明显，或者两组样本的量纲不一致等）

计算tips小费的方差与标准差

#计算小费的方差
var=tips.tip.var()
print('方差:',var)#方差: 1.914454638062471
#计算小费的标准差
std=tips.tip.std()
print('标准差:',std)#标准差: 1.3836381890011822

2.2.数据的分散趋势-极差与四分位差

• 极差是指数值型变量的最大值与最小值之间的差，体现的是数据范围的跨度，数值越大，数据越分散，反之越集中
• 四分位差是上四分位与下四分位数之间的差，反映的是中间50%数据的离散程度，数值越大，说明中间部分的数据越分散，反之越集中

2.3.数据的分散趋势-变异系数

• 当需要比较两组数据的分散程度时，如果两组数据的样本量悬殊，或者数据量纲不同，需要使用变异系数
• 变异系数能够消除样本量或量纲的影响，计算原理是将数据的标准差与算数平均值做商

以tips小费数据为例，分别计算男性顾客与女性顾客所支付消费的变异系数，进而对比两类人群在支付小费时的分散程度。

#筛选出男性顾客与女性顾客的小费数据
tip_man=tips.tip[tips.sex=='Male']
tip_women=tips.tip[tips.sex=='Female']
#统计男性顾客与女性顾客的样本量
print('男性顾客的样本量为：',len(tip_man))#男性顾客的样本量为： 157
print('女性顾客的样本量为：',len(tip_women))#女性顾客的样本量为： 87
#计算男性顾客与女性顾客所支付小费的变异系数
cv_man=tip_man.mean()/tip_man.std()
cv_woman=tip_women.mean()/tip_women.std()
print('男性顾客的变异系数：',cv_man)#男性顾客的变异系数： 2.074819737425079
print('女性顾客的变异系数：',cv_woman)#女性顾客的变异系数： 2.443692716795204

• 由于男性与女性顾客的样本量存在一定差异，所以只能选择变异系数来衡量两者在支付小费上的分散程度
• 从变异系数的计算结果可知，女性的变异系数比男性大，说明女性所支付的小费更加分散

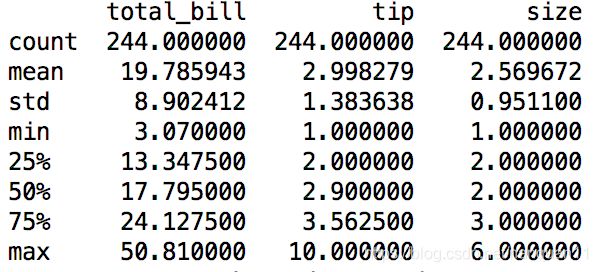
2.4.数据的分散趋势-describe方法

默认对所有数值型变量做汇总统计

tips.describe()

通过制定include参数可以实现离散型变量的统计汇总

tips.describe(include=['object'])

3.数据的分布形态

• 数据的分布形态反映的是数据的形体特征，如密度曲线表现为高矮胖瘦、非对称等特点
• 统计学中最典型的数值型分布为正态分布，其密度曲线呈现为中间高两边低、左右对称的倒钟形状
• 对于数据的分布形态可以通过计算其偏度和峰度指标，进而得到数据是否近似正态分布或者是否存在尖峰厚尾的特征

以经典的森林火灾为例：

orestfires=pd.read_csv('forestfires.csv',sep=',')

计算受灾面积（area变量）的偏度和峰度值，从而分析出受灾面积数据的分布特征

#计算受灾面积的偏度
print('偏度为：',forestfires.area.skew())#偏度为： 12.846933533934866
#计算受灾面积的峰度
print('峰度为：',forestfires.area.kurt())#峰度为： 194.1407210942299

由此可知：

• 受灾面积的偏度为12.847>0，数据表现为右偏的特征，说明少部分森林面积受灾面积非常大
• 受灾面积的峰度为194.141>0，则说明数据具有尖峰的特征，主要的受灾面积集中在某个小范围数值内

偏度和峰度的计算，是从定量的角度判断数据的分布特征，同时，还可以通过绘制直方图直观地放映出数据的体态特征，以及绘制受灾面积的实际密度分布曲线和理论的密度分布曲线

sns.set(font=getChineseFont(8).get_name())
sns.distplot(a=forestfires.area,
                 fit=stats.norm,#指定绘制理论的正态分布曲线
                 norm_hist=True,#绘制频率直方图
                 hist_kws={
     'color':'steelblue','edgecolor':'black'},#设置直方图的属性（填充色和边框色）
                 kde_kws={
     'color':'black','linestyle':'--','label':'核密度曲线'},#设置核密度曲线的属性
                 fit_kws={
     'color':'red','linestyle':':','label':'正态密度曲线'}#设置理论正态分布曲线的属性
                 )

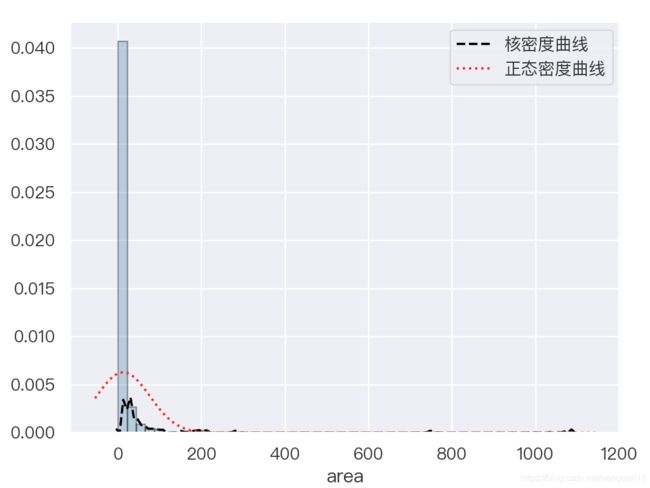直方图所呈现的效果为严重右偏，绝大多数的受灾面积为50个单位以内，两条曲线吻合度不高，所以该数据的分布并非正态分布。

4.数据的相关关系

• 变量之间是否存在某种相关或依存关系，如气温升高与空调销量之间的关系等
• 一般而言，在判断变量之间的相关性时，可以选择最为直观的散点图
• 还可以通过计算两个变量之间的相关系数来判断变量之间的相关性，通过这种定量的方法，可以得知变量之间相关性的高低
• 通过公式得到的相关系数取值范围在-1到+1：如果绝对值越接近于1，则说明两个变量之间的线性相关程度越强，如果绝对值越接近于0，则辨识两个变量之间的线性相关程度就越弱
• 关系数绝对值>=0.8，高度相关；0.5<=相关系数绝对值<0.8，中度相关；0.3<=相关系数绝对值<0.5，弱相关；相关系数绝对值<0.3，几乎不相关

以锅炉发电为例，其中PE表示发电量，其余变量是可能影响发电量的因素（AT表示炉内温度、V表示炉内压力、AP表示炉内的相对湿度、RH表示锅炉的排气量）

ccpp=pd.read_excel('C_C_P_P.xlsx')

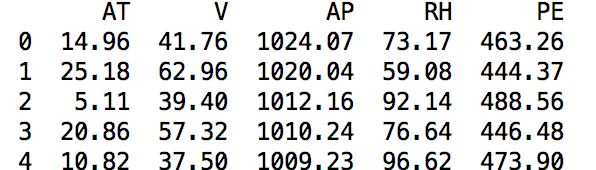使用corrwith方法计算PE变量与其余变量之间的相关系数

ccpp.corrwith(ccpp.PE)

由此可知：发电量PE与炉内温度AT、炉内压力V之间存在高度相关关系，并且呈负相关；发电量与炉内相关湿度AP之间存在中度相关关系，与锅炉排气量RH之间存在弱相关。

如AT与PE之间的散点图：

绘制整个ccpc数据集中两两变量之间的散点图

sns.set(font=getChineseFont(8).get_name())
sns.pairplot(ccpp)

矩阵的下三角部分反映了数值型变量之间的两两散点关系（如RH变量与V变量之间几乎不存在相关性，AT变量与V变量之间呈现一定的正相关关系），矩阵的对角线上则是单变量的直方图（例如AP变量呈现近似正态分布的特征，RG变量呈现左偏的分布特征）。

绘制整个ccpc数据热力图

corr = ccpp.corr()
sns.heatmap(corr,xticklabels=corr.columns.values,yticklabels=corr.columns.values)

从图中配合颜色可以看出：颜色越深或越浅，则相关系数越高

5.数据的波动趋势

数据的波动趋势主要反映的是某个数值型变量随时间的推移，它所表现出来的波动特征

• 对于波动特征的解释往往可以拆分为趋势线波动（即数据呈现波浪式上升或下降的特征）、季节性波动（即数据随着季节性因素呈现有规律的波动特征）和周期性波动（即数据随着认为的周期性因素呈现有规律的波动特征，如各大电商定期搞的促销活动，导致数据的周期性波动）
• 对于数据波动趋势的刻画，可以借助于折线图直观地呈现

三.数据的推断

数据的推断是对数据深层次的探索或挖掘，用于验证数据是否服从某种假设。

1.正态性检验

统计学中的很多模型或检验都需要数据满足正态分布的假设前提，例如线性回归模型中假设残差项服从正态分布（因变量y服从正态分布），两样本之间的t检验或多样本之间的方差分析均要求样本服从正态分布，所以在碰到这些模型或检验时就需要验证样本是否服从正态分布。

• 两种方法：一类是定性的图形法（直方图、PP图或QQ图）；另一类是定量的统计法（Shapiro检验、K-S检验等）

1.1.直方图法

见前文“数据的分布形态”部分

1.2.PP图与QQ图

• PP图的思想是对比正态分布的累计概率值和实际分布的累计概率值
• QQ图比对正态分布的分位数和实际分布的分位数
• 利用它们判断变量是否近似服从正态分布的标准是：如果散点比较均匀地散落在斜线上，则说明变量近似服从正态分布，否则就认为数据不服从正态分布

由于QQ图更为常见，本例使用QQ图判断数据是否服从正态分布

pp_qq_plot=sm.ProbPlot(sec_buildings.price)
#绘制QQ图
pp_qq_plot.qqplot(line='q')
plt.title('Q-Q图')

由图可知：图形中的散点并没有均匀地分布在倾斜线附近，右侧的散点与倾斜线之间有较大的偏离，说明数据存在严重的右偏特征，因此，数据并不服从正态分布。

1.3.Shapiro检验法和K-S检验法

当图形展现为模棱两可的状态时，变需要使用定量化的统计方法

• Shapiro检验法和K-S检验法均属于非参数的统计方法，它们的原假设被设定为变量服从正态分布
• 样本量低于5000时，Shapiro检验法比较合理，否则应使用k-S检验法
• scipy模块下的子模块stats提供了专门的检验函数，分别是shapiro函数和kstest函数可以用于Shapiro检验法和K-S检验法

print(sec_buildings.shape)#(20275, 9)

超过5000个样本，选择K-S检验

result=stats.kstest(rvs=sec_buildings.price,
                        args=(sec_buildings.price.mean(),sec_buildings.price.std()),#利用实际数据的均值和标准差设定理论的正态分布
                        cdf='norm'#指定累计分布函数为正态函数
                        )
print(result)#KstestResult(statistic=0.1683380890487141, pvalue=0.0)                        

元祖中第一个元素时K-S检验的统计量值，第二个元素时对应的概率值P，由于P近似为0，其远远小于默认的置信水平0.05，故需要拒绝二手房总价服从正态分布的原假设，进而从定量的角度得出其不服从正态分布的结论。

使用Shapiro检验法

#生成正态分布和均匀分布随机数
x1=np.random.normal(loc=5,scale=2,size=3500)
x2=np.random.uniform(low=1,high=100,size=4000)
#正态性检验
Shapiro_Test1=stats.shapiro(x=x1)
Shapiro_Test2=stats.shapiro(x=x2)

查看检验结果：
对于正态分布随机数x1的检验p值大于置信水平0.05，接受原假设；对于均匀分布随机数x2的检验P值远远小于0.05，拒绝原假设

2.卡方检验

用于离散型变量之间的探索性分析，如两个离散变量之间是否相互独立

• 卡方检验属于非参数的检验方法，其原假设是两个离散变量之间不存在相关性
• 该检验方法比较理论频数和实际频数之间的吻合程度，两者的吻合度越高，则认为两个离散变量越不相关
• 实际频数是指两个离散变量的组合频数，理论频数则为期望频数

探究蘑菇的形状cap_shape与其是否有毒type之间的关系：

mushrooms=pd.read_csv('mushrooms.csv',sep=',')

构造两个离散型变量之间的频次统计表（或列联表）

crosstable = pd.crosstab(mushrooms.cap_shape,mushrooms.type)

卡方检验

result=chi2_contingency(crosstable)

返回四部分结果分别为卡方统计量（489.92），概率P值（1.196 e-103）、自由度（5）和理论频率表。
p值为1.196 e-103，远小于0.05，故拒绝原假设，认为蘑菇的形状与其是否有毒存在一定的相关性

3.t检验

矿泉水平均含量是否为550ml；两个年级学生的平均实例水平是否存在一定差异；从平均水平看，药物对患者病情的治疗是否存在前后差异——对于以上类似的问题，需要用到t检验，该方法主要用于对比两个平均值之间是否存在显著的差异。

3.1.单样本t检验

也称为样本均值和总均值的比较性检验，对于该检验方法而言，要求样本满足两个前提假设，分别是样本服从正态分布假设，以及样本之间满足独立性假设（即样本之间不存在相关性）
对比计算的t统计量和理论t分布的临界值，如果统计量的值大于临界值，则拒绝原假设（即认为样本均值与总体均值之间存在显著的差异），否则接受原假设。

有如下饮料净含量数据：

data=[558,551,542,557,552,547,551,549,548,551,553,557,548,550,546,552]

进行单样本t检验

result=stats.ttest_1samp(a=data,#指定待检验的数据
                             popmean=550,#指定总体均值
                             #hiding缺失值的处理办法（如果数据中存在缺失值，则检验结果返回nan）
                             nan_policy='propagate')

结果为：

Ttest_1sampResult(statistic=0.7058009503746899, pvalue=0.49112911593287567)

概率P值大于0.05，故不能拒绝原假设，即认为饮料净含量的检验结果是合格的

3.2.独立样本t检验

是针对两组不相关样本（各样本量可以相等也可以不相等），检验它们在某数值型指标上均值之间的差异

• 同样需要满足两个前提假设，即样本服从正态分布，且样本之间不存在相关性
• 与单样本t检验相比，还存在一个非常重要的差异，就是构造t统计量时需要考虑两组样本的方差是否满足齐性（即方差相等）

以小费数据tips为例，通过t检验判断男女顾客在支付消费金额上是否存在显著差异。

tip_man=tips.tip[tips.sex=='Male']#男性客户支付的小费
tip_women=tips.tip[tips.sex=='Female']#女性客户支付的小费

检验两样本之间的方差是否相等

result=stats.levene(tip_man,tip_women)

结果为：

LeveneResult(statistic=1.9909710178779405, pvalue=0.1595236359896614)

P值大于0.05，说明两组样本之间的方差满足齐性，所以在计算t统计量的值时，应该选择方差相等所对应的公式

进行两独立样本的t检验：

result=stats.ttest_ind(a=tip_man,b=tip_women,
                           equal_var=True#指定样本方差相等
                           )

结果为：

Ttest_indResult(statistic=1.3878597054212687, pvalue=0.16645623503456763)

p值大于0.05，故接受原假设，即认为两独立样本的均值不存在显著的差异。

3.3.配对样本t检验

针对同一组样本在不同场景下，某数值型指标均值之间的差异。

• 即单样本t检验，检验的是两配对样本差值的均值是否等于0，如果等于0，则认为配对样本之间的均值没有差异，否则存在差异
• 该检验也遵循两个前提假设，即正态性分布假设和样本独立性假设

以我国各省2016年和2017年的人均可支配收入数据为例，判断2016年和2017年该指标是否存在显著差异。

计算两年人均可支配收入之间的差值

diff=ppgnp.ppgnp_2017-ppgnp.ppgnp_2016

使用ttest_1samp函数计算配对样本的t统计量

result=stats.ttest_1samp(a=diff,popmean=0)

结果为：

Ttest_1sampResult(statistic=13.98320645741795, pvalue=1.1154473504425075e-14)

使用ttest_rel函数计算配对样本的t统计量

result=stats.ttest_rel(a=ppgnp.ppgnp_2017,b=ppgnp.ppgnp_2016)

结果为：

Ttest_1sampResult(statistic=13.98320645741795, pvalue=1.1154473504425075e-14)

对比结论：无论采用单样本的t检验法还是采用配对样本的t检验法，得到的t统计量都是相同的。因此，从结果来看，概率p值远远小于0.05，故不能接受原假设，即认为两年人均可支配收入使存在显著差异的。