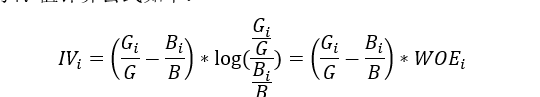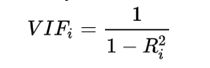评分卡模型变量筛选

变量筛选

用户的属性很多，如果全部输入模型，时间开销太大，而且模型复杂度过高。也会导致模型泛化能力降低，需要提前剔除没有意义的变量。

挑选入模变量需要考虑很多因素，比如：变量的预测能力，变量之间的线性相关性，变量的简单性（容易生成和使用），变量的强壮性（不容易被绕过），变量在业务上的可解释性（被挑战时可以解释的通）等等。

其中最主要和最直接的衡量标准是变量的预测能力和变量的线性相关性。本文主要探讨基于变量预测能力的单变量筛选，变量两两相关性分析，变量的多重共线性分析。

变量筛选的目的和作用

（1）剔除和目标变量不太相关的特征
（2）消除多重共线性的影响
（3）增加解释性

变量筛选的方式

（1）变量挑选
（2）降低维度
注意：变量挑选这是降低维度的其中一种方式，降低维度最有名的是：主成分分析法（PCA），PCA只是降低维度，并没有剔除变量特征

变量挑选常用手段

 基于IV值的变量筛选
 基于LASSO正则化的变量筛选
 基于stepwise的变量筛选
 基于特征重要度的变量筛选：RF, GBDT，XGboost…

1.单变量筛选

单变量的筛选基于变量预测能力，常用方法：

1.1基于IV值的单变量筛选

① 用IV值检验有效性
IV值（信息价值(information value)），是目前评分卡模型中筛选变量最常用的指标之一。

自变量的IV值越大，表示自变量的预测能力越强。类似的指标还有信息增益、基尼(gini)系数等。常用判断标准如下：

变量第i个分箱的IV值计算公式如下：

特征信息度IV的作用：
（1）高IV表示该特征和目标变量的关联度高
（2）不能盲目追求过高的IV，过高的IV，可能有潜在的风险
（3）特征分箱越细，IV越高
（4）实际应用过程，IV满足一个阈值，即可保留该变量，常用阈值如下：
<=0.02: 没有预测性，不可用
0.02 to 0.1: 弱预测性
0.1 to 0.2: 有一定的预测性
0.2 +: 高预测性
（这里注意，一般银行里面数据质量比较好，可以设置IV的阈值为0.2，但是其他机构，数据，数据质量没有那么好，可以设置IV的阈值为0.1,0.02的比较低的阈值）
0.8+：IV超过0.8一般是不可取的

1.2基于stepwise的变量筛选

基于stepwise的变量筛选方法也是评分卡中变量筛选最常用的方法之一。具体包括三种筛选变量的方式：
**（1）前向选择forward：**逐步将变量一个一个放入模型，并计算相应的指标，如果指标值符合条件，则保留，然后再放入下一个变量，直到没有符合条件的变量纳入或者所有的变量都可纳入模型。

**（2）后向选择backward：**一开始将所有变量纳入模型，每次剔除‘最差’的变量，该变量的剔除使得模型效果变化最不显著，评估模型的性能改善。持续此过程，直到没有变量剔除后，模型效果的的变化不显著。

**（3）逐步选择stepwise：**该算法是向前选择和向后选择的结合，逐步放入最优的变量、移除最差的变量。

注意：评分卡模型中不常用这种变量筛选的方法，更倾向于lasso正则化变量筛选。主要原因：①逐步回归法耗费时间长，筛选较慢；②python中没有相关包

1.3基于特征重要性的变量筛选

基于特征重要度的变量筛选方法是目前机器学习最热门的方法之一，其原理主要是通过随机森林和GBDT等集成模型选取特征的重要度。

①随机森林计算特征重要性步骤：
1）对每一颗决策树，选择相应的袋外数据（OOB）计算袋外数据误差，记为errOOB1（所有树的误差均值）；
2） 随机重拍每个特征，当某个特征在策树中的顺序改变后，计算袋外数据误差，记为errOOB2（所有树的误差均值）。
3） 对每个特征计算其更换前后，袋外误差前后差的均值（errOOB1- errOOB2），如果袋外误差改变较大，说明该特征重要度比较高。

②GBDT计算特征重要性步骤：
特征 j 在单颗树中的重要度的如下：

其中，L 为树的叶子节点数量，L-1 为树的非叶子节点数量，V_t 是和节点 t 相关联的特征，i_t^2是节点 t 分裂之后平方误差的减少值。
特征j的全局重要度为特征j在单颗树中的重要度的平均值：

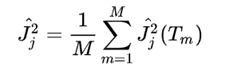
其中，M 是树的数量。

1.4 基于LASSO正则化的变量筛选

L1正则化通常称为Lasso正则化，它是在代价函数上增加了一个L1范数：

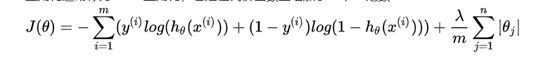
为什么L1正则化可以进行变量筛选？
以现行回归为例：

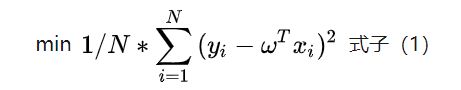
加入L1正则化（Lasso）

加入L2正则化（岭回归）

假设一组样本是二维的，那么对应的参数也是二维

• 加入正则化以后
  
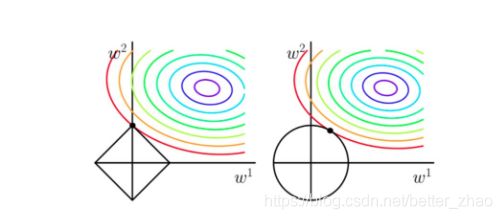
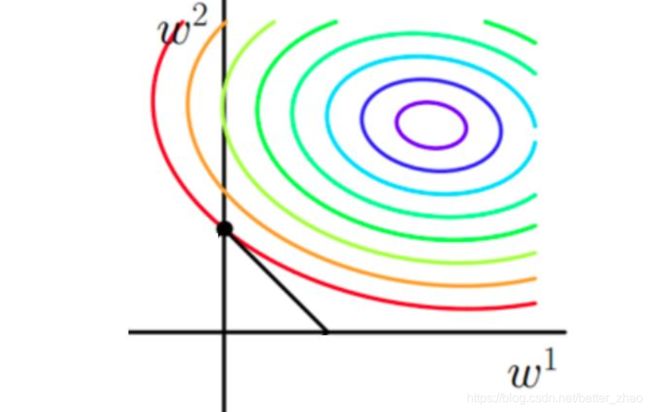
  从上边两幅图中我们可以看出：
• 如果不加L1和L2正则化的时候，对于线性回归这种目标函数凸函数的话，我们最终的结果就是最里边的紫色的小圈圈等高线上的点。
• 当加入L1正则化的时候，我们先画出 | w1+w2| = F 的图像，也就是一个菱形，代表这些曲线上的点算出来的 1范数*| w1+w2| 都为F。那我们现在的目标是不仅是原曲线算得值要小（越来越接近中心的紫色圈圈），还要使得这个菱形越小越好（F越小越好）。那么还和原来一样的话，过中心紫色圈圈的那个菱形明显很大，因此我们要取到一个恰好的值。
  

以同一条原曲线目标等高线来说，现在以最外圈的红色等高线为例，我们看到，对于红色曲线上的每个点都可以做一个菱形，根据上图可知，当这个菱形与某条等高线相切（仅有一个交点）的时候，这个菱形最小，上图相割对比较大的两个菱形对应的1范数更大。
所以，最终加入L1范数得到的解，一定是某个菱形和某条原函数等高线的切点。

经过观察可以看到，几乎对于很多原函数等高曲线，和某个菱形相交的
时候及其容易相交在坐标轴（比如上图），也就是说最终的结果，解的
某些维度及其容易是0，比如上图最终解是 (0,x)，基于此可以进行特征选择

2. 多变量分析

避免由于共线性，造成造模的不便

2.1 变量两两相关性分析

当相关性高时，只能保留一个：
·选择IV高的
·选择分箱均衡的

对于自变量X_1，X_2如果存在常数 c_0，c_1，c_2 使得以下线性等式近似成立：
c_1 X_1+c_2 X_2≈c_0
称自变量X_1，X_2如具有较强的线性相关性。

两变量间的线性相关性可以利用皮尔森相关系数来衡量。系数的取值为 [-1.0,1.0] ，相关系数越接近0的说明两变量线性相关性越弱，越接近1或-1两变量线性相关性越强。

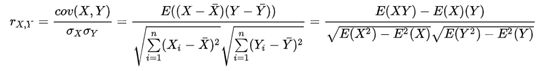
当两变量间的相关系数大于阈值时（一般阈值设为 0.7 或 0.4），剔除IV值较低的变量，或分箱严重不均衡的变量。

2.2 变量的多重共线性分析

对于自变量X_1，X_2 …. X_n如果存在常数 c_0，c_1，c_2 …. c_n使得以下线性等式近似成立:
c_1 X_1+c_2 X_2+⋯c_n X_n ≈ c_0

称自变量X_1，X_2…X_n如具有较强的线性相关性。

通常用 VIF 值来衡量一个变量和其他变量的多重共线性：

当某个变量的 VIF 大于阈值时（一般阈值设为10 或 7），需要逐一剔除解释变量。当剔除X_k发现VIF低于阈值，从X_i，X_k中剔除IV值较低的一个。

总结一下变量筛选的意义：
1 剔除跟目标变量不太相关的特征
2 消除由于线性相关的变量，避免特征冗余
3 减轻后期验证、部署、监控的负担
4 保证变量的可解释性