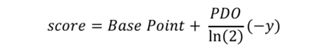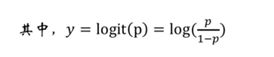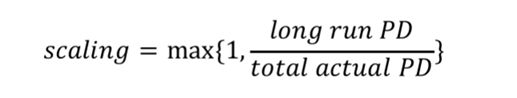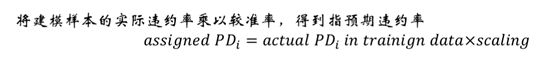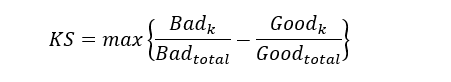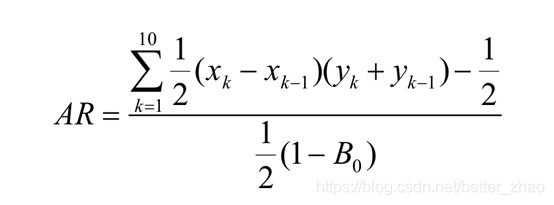违约预测模型后续工作
一、 从概率到分数
1、评分卡分数计算
逻辑回归模型得到两个信息,一是哪些特征是比较重要的,二是每个客户是否会违约的一个概率。至此模型并不是直接就能用了。实际我们不会直接用这个概率,而是将其映射到一些分数段当中。
(1)计算公式:
上述p:指违约概率:p越大,p/(1-p)越大,y越大,Base Point减去一个大的数,那score就会越小。就是说,违约概率p越大,最后的分数score越小,这个和实际逻辑也是相通的。
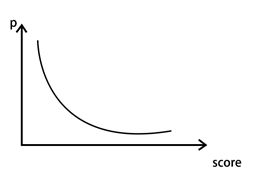
·Base Point:基准分,没有实际意义
·PDO:points to double odds:好坏比每升高一倍,评分增加一个PDO单位
好坏比:好样本/坏样本=(总样本-坏样本)/坏样本=总样本/坏样本-1=1/(坏样本/总样本)-1=1/p-1
这句话的证明过程如下:

分数一般是个整数,小数是没有意义的。
2、评分卡分数分级
在评分模型中,得到分数后需要对分数进行分级操作,将人群划分到有限的几个组别中。
划分方法:
将分数视为连续变量,采用监督式方法,例如best-KS或者ChiMerge进行有序划分,且一般划分为10组。
将最后计算得到的评分进行分层,持续跟踪表现期,每一层的实际违约率:

例如:2018年4月28号这一批人群,到2019年4月8号,有了完整的一年观察期。将2018年4月28号的100人分为5组,共有10人触发了坏样本定义的窗口,发生了逾期。实际违约率就是10%。
通常一组样本中,申请者申请的日期不会超过半年,就是说这一组样本中,最早申请的日期和最晚申请的日期跨度不超过半年。有个问题:
另外同时获取过去较长时间内(比如5~10年)的长期实际违约率(long run PD),以此为基准,得到校准率:
实际群体的违约率是有一个经济周期现象的,如果我拿到一个长期的违约率比短期违约率还低,那这个系数scaling我会选择1,如果长期违约率比这个短期违约率高,那选在后者。也就是说,在风控行业,我会选择将实际情况往坏处想,就是事先将情况想得严重一些。
预期违约率:
不同组别中中,分数越高,逾期率月底,同一分数组中,逾期违约率高于实际逾期率。
二、模型的验证与监控
1、模型验证
评分卡模型训练完之后,需要在验证集上进行验证(模型验证实际上是模型开发的一个环节)。
通常,需要选择跟训练样本所在的日期不同的日期的申请样本做为验证集,称为OOT(out of date test)。这是为了验证模型在时间上的效力跟稳定性。
举例说明OOT:
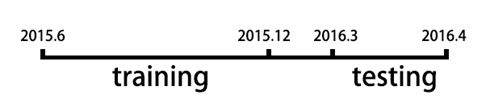
但是,训练样本也不能选2013年左右,相比测试样本时间跨度太长。宏观经济因素和国家政策对模型的影响也很大。不能说明是模型不稳定
2、模型监控
模型在部署并执行后,需要定期对模型的表现进行监控,以保证模型的各项性能不会出现
恶化。
- 定期:银行一般是一个月监控一次,三个月向高层进行汇报
- 互联网金融公司:每周都要监控
当某项指标持续恶化时,需要按需对模型进行调整甚至重新开发。
调整:可能是调整一些变量的计算逻辑,或者是参数进行约束,如果这样还不能使模型稳定,估计需要重新开发模型。重新搜集不同时间段的样本,搜集不同的数据,对同一个产品搜集不同的人群信息,从头开始建立评分卡。
模型性能报表中:用红灯,黄灯,绿灯代表一次监控事件的结果:
- 如果模型各项指标正常,我们给一个绿灯;
- 模型某次有一次警告,warning黄灯;
- 模型持续恶化error红灯
模型的监控与验证基本是一致的,主要包含了对模型稳定性、准确性和排序性的监测。
模型的监控指标
// 模型对违约和非违约人群的区分度
-
评分卡的目的
尽可能区分出潜在逾期人群和非逾期人群 -
区分人群的手段
评分卡分数的高低,一般认为分数高的逾期概率比较低 -
衡量区分能力的指标
(1)KS,阈值=30%,KS值越高表明区分能力越强(见)
(2)Gini Score
(3)Divergence Score
以上衡量指标都是衡量好坏人群的区分度
KS
将样本按照分数由低到高排序,X轴是总样本累计比例,Y轴是累积好,坏样本的比例,两条曲线在Y轴方向上相差最大的值即KS。
Badk和Goodk分别为累计到第K个分位点的坏样本个数和好样本个数
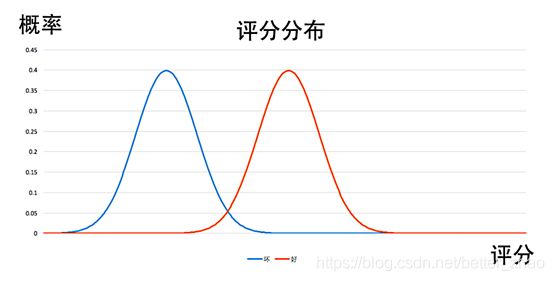
分数很低的所有样本中,大多数样本是被判定为坏样本,只有极少数样本被评定为好样本,所以坏样本率大于好样本率,当分数逐渐增加,越来越多的样本被分为好样本,好样本率逐渐增加。分数继续增加,而高分段坏样本并不多,所以累计坏样本占比的增幅会逐渐变缓。KS越大,说明区区分好坏样本的能力越强。
KS值是在模型中用于区分预测正负样本分隔程度的评价指标。,每个样本的预测结果化为probability或者一个分数范围。从最小的probability或者最低分到最大的probability或者最高分,正负样本的累积分布。KS值为两个分布中,最大差值的绝对值。KS值的取值范围是[0,1]。通常来说,值越大,表明正负样本区分的程度越好。征信模型中,最期望得到的信用分数分布是正态分布,对于正负样本分别而言,也都期望是呈正态分布的样子。如果KS值过大,一般超过0.9,就可以认为正负样本分得过开了,不太可能是正态分布的,反而是比较极端化的分布状态(U字形,两边多,中间少),这样的分数就很不好,基本可以认为不可用。但如果模型的目的就是完美区分正负样本,那么KS值越大就表明分隔能力越突出。另外,KS值所代表的仅仅是模型的分隔能力,并不代表分隔的样本是准确的。换句话说,正负样本完全分错,但KS值可以依旧很高。
KS越大,说明模型的区分能力越好。
如果数据质量比较好(比如;银行),在训练的时候要求KS大于40%,在测试的时候KS大于30%,实际使用时KS大40%;
如果数据质量没有那么好(比如互金公司),可以放宽要求,训练的时KS大于30%,测试时不能再放宽了,KS还是要求大于30%。
Gini Score
比如对某个特征固定在开发和上线后,用等频划分方式查看划分效果。
Divergence Score(多样性评分)
μ_good:好样本分数均值
μ_bad: 坏样本分数均值
〖var〗_good: 好样方差均值
〖var〗_bad: 坏样方差均值
// 模型的准确度
评分模型通过分数的高低来判断申请者信用资质的好坏,意味着:
表现期内逾期人群的分数需要集中在低分段;
非逾期人群的分数需要集中在高分段;
形成一个“有序”的结果
1. AR
坏样本累计速度相对于全体样本累积速度的差异。
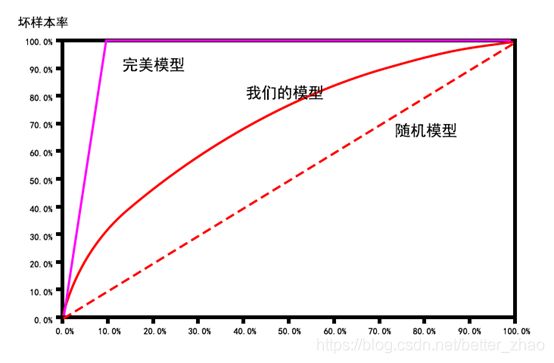
将样本按照分数从低到高排序,X轴是总样本的累计比,Y轴是坏样本占总样本的累计比例。
AR等于我们的模型在随机模型之上的面积除以理想模型在随机模型至上的面积(计算中可以用梯形逼近曲线下面积进行计算)
一个完美模型:在能够将所有的坏样本评分在低分段
任意随机模型:因为模型是随机的,所以不能很好地区分好样本,也因此坏样本累计占比和总样本的累计数呈线性关系(即对角线)
公式解析:
x_k表示累计总样本比例,x_k-x_(k-1),表示当前分位点累计总样本比例-上一个分位点总样本比例,实际上就是当前分位点的总样本比例
y_k表示当前分位点的坏样本比例,y_(k-1)表示上一个分位点的坏样本比例,那两个相加实际上就是当前分位点累计坏样本比例。
AR越大,我们的模型在随机模型之上的面积越接近完美模型在随机模型之上的面积,也说明模型区分准确度越高。
所以公式可以变换为:
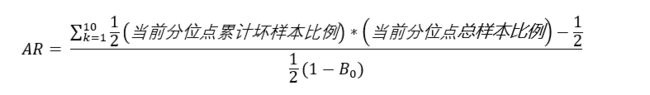
上述公式继续变换
1-B0 = 总的好样本比例
2. Kendal’s Tau
// 模型的稳定性
1. 人群分布的稳定
PSI取值越小,说明分数的分布随时间的变化越小。就是说,我在模型开发阶段,根据人群的属性和行为数据给他们相应打上了分数,如果模型足够稳定,随着时间的推移,不同分数段的人群个数变化不会太大。
如果PSI 小于25%(经验值),说明模型稳定;
如果PSI 小于40%,说明模型不太稳定;
如果PSI 大于40%,基本说明这个模型不稳定,不能用;
2. 逾期违约率的保守性
从风险评估的角度,预期违约率肯定会高于实际违约率(我们总是会事先将情况往坏处想的思想),这就叫做保守估计。
模型部署上线后,我们需要定期进行监控,如果第i组的实际违约率比我们预计的违约率要大的时候,我们需要做二项检验。
零假设H0: 预期违约率 > 实际违约率
非零假设H1: 预期违约率 < 实际违约率
比如一组200人的样本,观察到有20人发生逾期,实际逾期率=20/200=10%
但是当时我们建立模型的时候,根据当时的实际逾期率计算得到预期违约率为8%(从目前来看,观察期的实际违约率高于我的逾期违约率)
据此我们要进行二项检验,考察这个20人逾期导致的10%逾期率,这个时间是随机因素导致的随机事件还是必然时间。
在原假设成立的情况下,我根据预计8%的违约率,8%X200=16(平均下来应该是有16个人逾期),发生这个事情的概率是多少,如果概率大于置信度(0.05),则认为这个可能是一个随机事件,否则拒绝原假设。
3. 模型的部署
基于逻辑回归的评分卡模型在完成了开发、验证和审计后,可以进入到部署阶段。不同的
使用场景,应该选择不同的部署方式。
(1)实时计算
用于线上申请行为,且模型部分依赖于三方数据。当申请进件信息传入到部署模型的服务
器时,服务器会从后台数据库里实时查询相关信息(包括调用三方数据),将数据转换
成特征、完成分箱操作和WOE编码,带入模型。
• 优点:
准确度较高
• 缺点:
变量计算不宜涵盖太长的时间切片,且本机构、第三方数据源接口不能有延时
(2)非实时计算
用于线下申请行为。当申请进件信息传入到部署模型的服务器时,服务器会根据传入的数
据计算分数。
• 优点:
服务器并发压力小
可人工干预
特征跨度不受限制
缺点:
• 准确度较差,不能抓住突发事件(比如近期的多头)
4. 拒绝推断
模型开发时选择了一批人,用观察期数据预测表现期是否会发生逾期事件,只有用了我们的产品(比如借了钱,还了钱)的人群才会有表现期,才能去定义是好人还是坏人,有个问题,那些被我们拒绝的用户,模型开发的时不知道他的表现(因为之前被拒绝掉了,没有历史使用数据),模型使用时也不知道他的表现(因为这些用户被拒绝了,没有使用我们的产品)。只有在被我们准入的客户群体中才能检查评分卡模型的好坏。
评分卡模型在开发过程中,选取的数据都是历史申请准入后、有实际表现的数据。而在使用时,被准入的客户可以观测到实际表现,被拒绝的客户则无法推断。换言之,我们可以推断评分卡准入客户的好坏情况,却无法推断拒绝客户。
目前尚未有很好的办法解决这个难题,一般可以借鉴的有:
方法一
在审核阶段,随机抽取少量低分段人群给予准入,以此来推断评分卡在低分段人群的表现
代价:会有违约损失
方法二
跟踪被拒绝掉的客群在其他平台上的表现
代价:跟踪的成本极高
5. 评分卡的使用
(1)申请者的拒绝和准入
业务人员、风控人员根据评分卡的结果,对于申请进件准入或者拒绝。一般可以根据2条
原则进行准入分的设定:
对于非首次使用评分卡的机构
• 当以提高业务量为目标时,在不降低坏账率的前提下,降低现有的准入分
• 当以降低违约率为目标时,在保持跟之前的人数一样多的情况下,提高准入分
对于首次使用评分卡的机构
领导决定通过率!
(2)授信额度
四种额度:前三种是固定的,最后一个是我们根据模型计算得出的结果。
前三个额度是:基础额度、盖帽额度、托底额度
基础额度(base limit)B:对大部分人,信用卡的基础额度一般是2万元;
盖帽额度(hat limit)H:针对于信用比较好的人,可以适当提高一下额度,最高提高到盖帽额度,比如从2万提高到3万
托底额度(floor limit)F:对于信用资质比较差的人,可以适当降低额度,最低降低到托底额度。比如从2万降低到1万。
授予额度:第四种额度就是根据当前申请,我们给予的额度。
我们授予的额度取决于他的评分,评分低的人额度差,评分高的人额度高。评分的本质是概率。
评分最低区间对应的预期违约率是P_max,评分最高的区间对应的预期违约率是P_min
大部分人所在区间对应的预期违约率是P_O,如果某个申请进件的预期违约率是P_1,则该申请人的授信额度是:
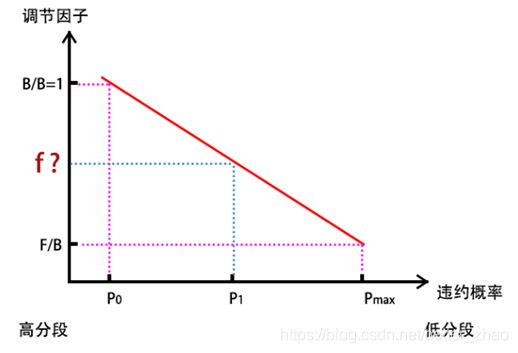
1)如果P_1> P_O
违约率最高P_max的位于最低分数段,在这段中,由于用户信用资质不高,通常会降低信用额度,最低降低到托底额度F,所以调节因子 f= F/B,额度 = f *B =F
绝大部分人的违约率为P_O,信用资质正常,不会过高,也不会过低,所以信用额度就是基础额度,调节因子 f= B/B = 1,额度= f*B = B
如果某个人的违约率在两者之间,也就是P_0< P_1< P_max,则调节因子计算过程如下

汇总如下:
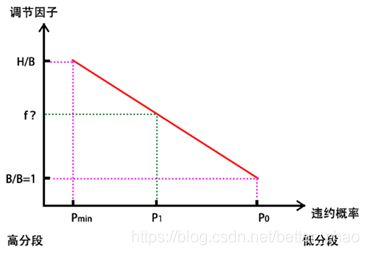
2)如果P_1< P_O
违约率最低P_min的位于最高分数段,在这段中,由于用户信用资质很高,通常会提升信用额度,最高提升高盖帽额度,所以调节因子 f= H/B,额度 = f *B =H
绝大部分人的违约率为P_O,信用资质正常,不会过高,也不会过低,所以信用额度就是基础额度,调节因子 f= B/B = 1,额度= f*B = B
如果某个人的违约率在两者之间,也就是P_min< P_1< P_0,则调节因子计算过程同上面一直,利用三角形相似度原理。
汇总如下:

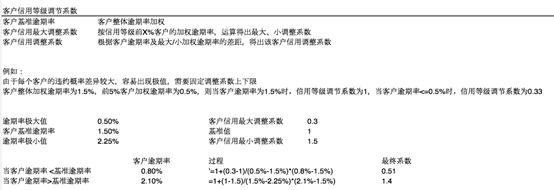
除了客户信用调节系数,其他都是业务上的系数。