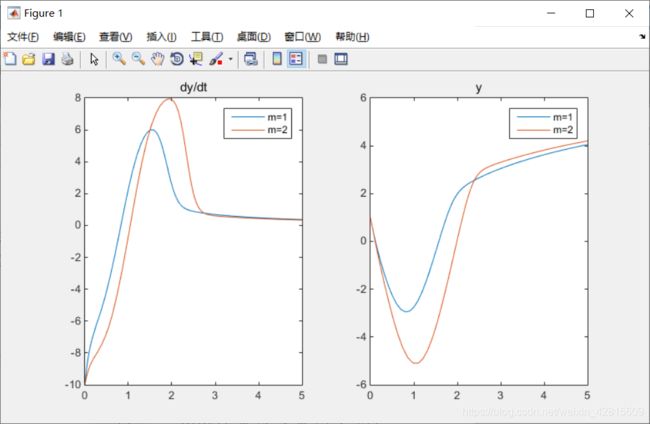
【matlab】ode45求解二阶微分方程,绘制曲线图 | 使用函数句柄的方法
朋友问题: 有微分方程如下:
m d 2 y d t 2 + d y d t e x p ( t ) − y 2 = 5 m \frac{d^2y}{dt^2} + \frac{dy}{dt} exp(t) - y^2 = 5 mdt2d2y+dtdyexp(t)−y2=5
其中, y ( t = 0 ) = 1 y(t=0)=1 y(t=0)=1, d y / d t ( t = 0 ) = − 10 dy/dt (t=0) = -10 dy/dt(t=0)=−10。
请在区间 [ 0 , 5 ] [0, 5] [0,5]内绘制两个子图,分别为 d y / d t dy/dt dy/dt与 y y y,每个子图涵盖 m = 1 m=1 m=1与 m = 2 m=2 m=2两种情况。
所以本题的核心问题在于:用数值计算的方法求解该方程,得到各点,绘制点图。
使用 matlab 自带的 ode45 ,方程组用句柄表示。
ode45 参见教程:如何使用ODE45
首先把题目方程转换,转换为 ode45 能理解的方式。
先声明变量:
y 1 = y y 2 = y ′ \begin{aligned} y_1 & = y \\ y_2 & = y' \\ \end{aligned} y1y2=y=y′
于是整理方程:
y 1 ′ = y 2 y 2 ′ = 1 m ( 5 − y 1 ′ e y 1 + y 1 2 ) \begin{aligned} y_1' & = y_2 \\ y_2' & = \frac{1}{m} (5 - y_1' e^{y_1} + y_1^2) \end{aligned} y1′y2′=y2=m1(5−y1′ey1+y12)
于是我们知道,ode45中要有2个变量,且将其右边的式子分别表示出来,即:
dy = @(t, y)[y(2); (5 - y(2)*exp(y(1)) + y(1)^2)/m];
其中:
y(2)代表 y 1 ′ = y 2 y_1' = y_2 y1′=y2;(5 - y(1)*exp(y(2)) + y(2)^2)/m代表 y 2 ′ = 1 m ( 5 − y 1 ′ e y 1 + y 1 2 ) y_2' = \frac{1}{m} (5 - y_1' e^{y_1} + y_1^2) y2′=m1(5−y1′ey1+y12)。
接着,规定初值: y ( t = 0 ) = 1 y(t=0)=1 y(t=0)=1, d y / d t ( t = 0 ) = − 10 dy/dt (t=0) = -10 dy/dt(t=0)=−10。
y10 = 1;
y20 = -10;
规定自变量 t t t 范围:
tspan = [0, 5];
输入 ode45 则为:
[t, y] = ode45(dy, tspan, [y10, y20]);
整个题目的代码为:
% 表示该方程组
m = 1;
dy = @(t, y)[y(2); (5 - y(2)*exp(y(1)) + y(1)^2)/m];
y10 = 1;
y20 = -10;
tspan = [0, 5];
% m = 1
[t_m_1, y_m_1] = ode45(dy, tspan, [y10, y20]);
% m = 2
m = 2;
dy = @(t, y)[y(2); (5 - y(2)*exp(y(1)) + y(1)^2)/m];
[t_m_2, y_m_2] = ode45(dy, tspan, [y10, y20]);
% plot
subplot(1, 2, 1);
plot(t_m_1, y_m_1(:, 2));
hold on
plot(t_m_2, y_m_2(:, 2));
title('dy/dt')
legend('m=1','m=2')
subplot(1, 2, 2);
plot(t_m_1, y_m_1(:, 1));
hold on
plot(t_m_2, y_m_2(:, 1));
title('y')
legend('m=1','m=2')
顺便学了 ode45 ,不错。