本章主要介绍了神经元模型、一些典型的神经网络算法等
5.1 神经元模型
“神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,他的组织能够模拟生物神经系统对真实世界物体作出的交互反应”
神经网络中最基本的成分是神经元模型。沿用至今的“M-P神经元模型”:神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的链接进行传递,神经元接受到的总输入值与神经元的阙值进行比较,然后通过“激活函数”处理以产生神经元的输出。常用“Sigmoid函数”作为激活函数。许多这样的神经元按照一定的层次结构连接起来,就得到了神经网络。
5.2感知机与多层网络
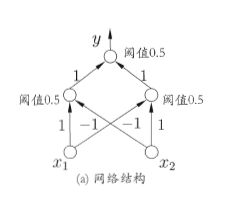
感知机由两层神经元组成,输入层接受外界输入信号后传递给输出层,输出层是M-P神经元,亦称“阙值逻辑单元”。感知机能够很容易地实现逻辑与、或、非运算。
给定训练集,权重ωi以及阙值θ可通过学习得到。阙值θ可看做一个固定输入为-1.0的“哑结点”,所对应的连接权重ωn+1,这样就统一为权重的学习。
感知机的学习规则:对训练样例(x,y),若当前感知机输出为 y^,则感知机权重:ωi ← ωi +Δωi Δωi = η(y - y^)xi;其中η属于(0,1)称为学习率。
感知机只有输出神经元进行激活函数处理,只拥有一层功能神经,学习能力非常有限。若两类模式线性可分,则感知机学习过程收敛,否则震荡。
要解决非线性可分问题,需考虑使用多层功能神经元。输入层与输出层之间的一层神经元被称为隐层或隐含层,隐含层和输出层神经元都是拥有激活函数的功能神经元。
多层前馈神经网络------每层神经元与下一层神经元全互联,神经元之间呢不存在同层连接,也不存在跨层连接。其中输入层神经元接受外界输入,隐层和输出层神经元对数据进行加工,最终结构由输出层神经元输出。
神经网络的学习过程,就是根据训练数据来调整神经元之间的连接权以及每个功能神经元的阙值;即神经网络学到的东西,蕴含在连接权与阙值中。
5.3误差逆传播算法
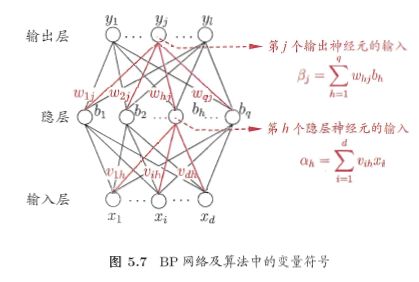
多层网络的学习能力比单层感知机强得多,欲训练多层网络,需更强大的学习算法。误差逆传播(BP)算法就是其中最杰出代表。
对训练例(xk,yk),假定神经网络的输出为yjk = f(βj - θj) 则网络在(xk,yk)上的均方误差为
图中网络有(d+l+1)q+l个参数需要确定,BP是一个迭代学习算法,在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计,任意参数的更新估计式为 v ← v+Δv。
学习率η控制着算法每一轮迭代中的更新成长,若太大容易震荡,太小收敛速度又会变慢。
误差逆传播算法
| 输入:训练集D= {(xk,yk)}k=1m 学习率η 过程: 1:在(0,1)范围内随机初始化网络中所有连接值和阙值 2:repeat 3: for all(xk,yk)属于D do 4: 根据当前参数和式5.3计算当前样本的输出yk^ 5: 根据式5.10计算输出层神经元的梯度项 6: 根据式5.15计算隐层神经元的梯度项 7: 根据式5.11 - 5.14更新连接权与阙值: 8: end for 9:until 达到停止条件 输出:连接权与阙值确定的多层前馈神经网络 |
BP算法的目标是最小化训练集D上的累计误差。
标准BP算法:每次仅针对一个训练样例更新连接权和阙值,更新规则是根据单个的Ek推导而得;如果类似的推导出基于累计误差最小化的更新规则,就得到了累计误差逆传播算法。
标准BP算法和累计BP算法之间的区别类似于随机梯度下降与标准梯度下降之间的区别。
证明,只须一个包含足够多神经元的隐层,多层前馈网络就能以任意精度逼近任意复杂度的连续函数。
两种策略环节BP网络的过拟合:“早停”、“正则化”。早停:将数据分成训练集和验证集,训练集用来计算梯度、更新连接值和阙值,验证集用来估计误差,若训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权和阙值。“正则化”:在误差目标函数中增加一个用于描述网络复杂度的部分,例如连接权与阙值的平方和,则误差目标函数改变为 其中λ属于(0,1)用于对经验误差与网络复杂度这两项进行折中。
其中λ属于(0,1)用于对经验误差与网络复杂度这两项进行折中。
5.4 全局最小与局部极小
若用E表示神经网络在训练集上的误差,则他显然是关于连接权ω和阙值θ的函数。因此,神经网络的训练过程可看做一个参数寻优过程,即在参数空间中,寻找一组最优参数使得E最小。
参数空间内梯度为0的点,只要其误差函数值小于邻点的误差函数值,就是局部极小点;可能存在多个局部极小值,但只有一个全局极小值。
基于梯度的搜索是使用最广泛的参数寻优方法,我们从某些初始解出发,迭代寻找最优参数值。每次迭代中,我们先计算误差函数在当前点的梯度,然后根据梯度来确定搜索方向。由于负梯度方向是函数值下降最快的方向,因此梯度下降法就是沿着负梯度方向搜索最优解。若误差函数在当前点参数值为0,则已达到局部极小,更新量将为0,这意味着参数的迭代将在此停止。
如果误差函数仅有一个局部极小,则也就是全局最小;如果有多个局部最小,则需“跳出”局部极小,从而进一步接近全局最小:1.从多个不同的初始点进行搜索,这样就可能陷入不同的局部极小,从中选择最有可能接近全局最小的结果;2.使用“模拟退火”技术,在每一步都以一定概率接近比当前解更差的结果,接受“次优解”的概率要随着时间的推移逐渐降低,从而保证算法稳定;3.使用梯度随机下降,在计算梯度时加入了随机因素,即使陷入局部极小点,他计算出的梯度可能不为0,这样就有机会跳出局部极小继续搜索。
5.5其他常见的神经网络
5.5.1 RBF网络
RBF(径向基函数)网络,是一种单隐层前馈神经网络,它使用径向基作为隐层神经元激活函数,而输出层则是对隐层神经元的线性组合。RBF网络可表示为![]()
径向基函数是某种沿径向对称的标量函数,通常定义为样本x到数据中心ci之间欧氏距离的单调函数。具有足够多隐层神经元的RBF网络能以任意精度逼近任意连续函数。
训练RBF网络:1.确定神经元中心ci,常用的方式包括随机采样、聚类等;2.利用BP算法等来确定ωi和βi。
5.5.2 ART网络
竞争型学习是神经网络中一种常用的无监督学习策略,在使用该策略时,网络的输出神经元相互竞争,每一时刻仅有一个竞争获的神经元被激活,其他神经元的状态被抑制。这种机制亦称“胜者通吃”原则。
ART(自适应谐振理论)网络是竞争型学习的重要代表,该网络由比较层、识别层、识别阙值和重置模块构成。其中,比较层负责接收输入样本,并将其传递给识别层神经元。识别层神经元对应一个模式类,神经元的数目可在训练过程中动态增长以增加新的模式类。
在接受到比较层的输入信号后,识别层神经元之间相互竞争以产生获胜上神经元。竞争的最简单方式为:计算输入向量与每个识别层神经元所对应的模式类的代表向量之间的距离,距离最小者胜。获胜的神经元向其他识别层神经元发送信号,抑制其激活。若输入向量与获胜神经元所对应的代表向量之间的相似度大于识别阙值,则当前输入样本被归为该代表向量所属类别,同时,网络连接权将会更新,使得以后再接受到的相似输入样本是该模式类会计算出更大的神经类;若相似度不大于识别阙值,则识别模块在识别层增设一个新的神经元。
识别阙值对ART网络的性能有重要影响,识别阙值较高,输入样本会被分成比较多、比较精细的模式类,而如果识别阙值比较低,则会产生比较少,比较粗略的模式类。
ART比较好地缓解了竞争型学习中的“可塑性-稳定性窘境”,可塑性是指神经网络要有学习新知识的能力,而稳定性是指神经网络在学习新知识是要保持对旧知识的记忆。ART网络的重要优点:可进行增量学习或在线学习。
5.5.3 SOM网络
SOM(自组织映射)网络,是一种竞争学习型的无监督神经网络,它能将高维输入数据映射到低维空间,同时保持输入数据在高维空间的拓扑结构,即将高维空间中相似的样本点映射到网络输出层的邻近神经元。
SOM网络中的输出层神经元以矩阵方式排列在二维空间中,每一个神经元拥有一个权向量,网络在接受输入向量之后,将会确定输出层获胜神经元,它决定了该输入向量在低维空间的位置。SOM训练额目标就是为每个神经元找到合适的权向量,以达到保持拓扑结构的目的。
SOM的训练过程:在接收到一个训练样本后,每个输出层神经元会计算该样本与自身携带向量之间的距离,距离最近的神经元成为竞争获胜者,称为最佳匹配单元。最佳匹配单元及其邻近神经元的权向量将被调整,以使得这些权向量与当前输入样本的距离缩小,这个过程不断迭代,直至收敛。
5.5.4级联相关网络
一般的神经网络模型通常假定网络结构是事先固定的,训练的目的是利用训练样本来确定合适的连接权、阙值等参数。而结构自适应网络则将网络结构也当做学习目标之一。级联相关网络是结构自适应网络的重要代表。
级联相关网络有两个主要成分:“级联”和“相关”,级联是指建立层次连接的层级结构。在开始训练时,网络只有输入层和输出层,处于最小拓扑结构;随着训练的进行,新的隐层神将元逐渐加入,从而创建起层级结构。相关是指通过最大化新神经元的输出与网络误差之间的相关性来训练相关的参数。
与一般的前馈神经网络相比,级联相关网络无需设置网络层数、隐层神经元数目,且训练速度快,但其在数据较小时易陷入过拟合。
5.5.5 Elman网络
与前馈神经网络不同,“递归神经网络”允许网络中出现环形结构,从而可让一些神经元的输出反馈会来作为输入信号。使得网络在t时刻不仅与t时刻的输入有关,还与t-1时刻的网络状态有关,从而能处理与时间有关的动态变化。
Elman网络是最常用的递归神经网络之一,他的结构与多层前馈网络很相似,但隐层神经元的输出被反馈回来,与下一刻输入神经元提供的信号一起,作为隐层神经元在下一时刻的输出。
5.5.6 Boltzmann机
神经网络中有一类模型就是为网络状态定义一个能量,能量最小化时网络达到理想状态,而网络训练就是在最小化这个能量函数。Boltzmann机就是一种“基于能量的模型”。其神经元分为两层:显层与隐层。显层用于表示数据的输入与输出,隐层则被理解为数据的内在表达。Boltzmann机中神经元是布尔型的,只能取0/1两种状态,1表示激活,0表示抑制。若网络中的神经元不依赖于输入值得顺序进行更新,则网络最终达到Boltzmann分布。
Boltzmann机的训练过程就是讲每个训练样本视为一个状态向量,使其出现的概率尽可能大。