马踏棋盘(C语言版)——贪心算法详解(栈的应用数据结构)
文章目录
-
- 题目
- 数据定义
- 程序各函数
- 主要思想
- 流程图
- 输出分析
- 源码
- 暴力和简单贪心
马踏棋盘是栈的一个十分经典的应用,最基本的完成思路其实就是深度优先搜索(dfs),是一种十分暴力的处理方式,费时费力还不一定可以得到一个好的结果。使用贪心算法,将每一步,每一步的下一步都进行贪心,便会节省大量的时间,而且成功率十分客观,现就马踏棋盘的一种贪心算法做以下总结
题目
设计一个国际象棋的马踏遍棋盘的演示程序。将马随机放在国际象棋 8x8 棋盘 Board[8][8]的某个方格中,马按走棋规则进行移动。要求每个方格只进入一次,走遍棋盘上全部 64 个方格。编制递归或非递归程序,求出马的行走路线,并按求出的行走路线输出。
(1)将行走路线以坐标的形式输出。
(2)在方阵中输出 1~64 个行走足迹;
数据定义
#include值得注意的是,结构体中,x_adr 其实是真实的纵坐标,y_adr 其实是真实的横坐标(大家画个数组表示的棋盘,其实就懂了)。这个首先要明确,不然在后面的定义和赋值等操作时,会有很多不便。
程序各函数
//初始化数据
void init();
//debug 打印栈的情况
void print_stack();
//入栈
void push_stack(int x_real,int y_real);
//出栈
void pop_stack();
//标记位置
void mark_chess(int x,int y);
//打印路径
void print_chess_board();
//打印每一步的位置
int t = 1;
void print_steps();
//马踏棋盘(贪心)算法
void run_horse_tanxin();
主要思想
我们算法最核心的部分,是在下一步到底应该如何选择这件事上,主要的贪心思路就是:
我们先判断下一步都有哪些位置可以走,然后我们再判断其可走位置的再下一步,有几个位置可以走,并统计这几个末端位置的在下一步有几个位置可以走。
也就是 分别计算当前位置下下一步的权,之后我们将下下一步的权都加起来,算成下一步的权,并存储到 next 数组里面。
之后,我们建立 real_next 数组,通过查找遍历,依次将 next 中最小元素的下标赋值给 real_next 数组,这样,我们就得到了一个下一步走的方向顺序的数组 real_next。
这时,我们就可以开始按照 real_next 的顺序来走下一步
以下是核心代码(注释已加):
//现在位置
x_now = Adr_Stack[top].x_adr;
y_now = Adr_Stack[top].y_adr;
//对方向进行排序
int next[ROW] = {
};
for(int i = 0;i < ROW;i++){
//下一步坐标
int x_next = x_now + dir[i][0];
int y_next = y_now + dir[i][1];
if((x_next > 0 && x_next <= COL) && (y_next > 0 && y_next <= ROW) && chess[y_next][x_next] == 0 ){
//对下一步的下一步判断是否可以走
for(int j = 0;j < ROW;j++){
int x_next_next = x_next + dir[j][0];
int y_next_next = y_next + dir[j][1];
//可以走,next 对应下标+1
if((x_next_next > 0 && x_next_next <= COL) && (y_next_next > 0 && y_next_next <= ROW) && chess[y_next_next][x_next_next] == 0){
next[i]++;
}
}
}
}
//依次返回 next 中最小元素的下标,返回后将元素赋值为最大
int real_next[8] = {
0};
int k = 0;
int t = ROW + 1;
for(int i = 0;i < ROW;i++){
t = ROW + 1;
for(int j = 0;j < 8;j++){
if(next[j] < t){
real_next[i] = j;
t = next[j];
k = j;
}
}
next[k] = ROW + 1;
}
//走下一步
int dir_now = 0;
for(dir_now = Adr_Stack[top].direction + 1;dir_now < ROW;dir_now++){
int x_real = x_now + dir[real_next[dir_now]][0];
int y_real = y_now + dir[real_next[dir_now]][1];
Adr_Stack[top].direction += 1;
if((x_real <= COL && x_real > 0) && (y_real <= ROW && y_real > 0) && chess[y_real][x_real] == 0){
//入栈
push_stack(x_real,y_real);
//标记棋盘
mark_chess(x_real,y_real);
break;
}
}
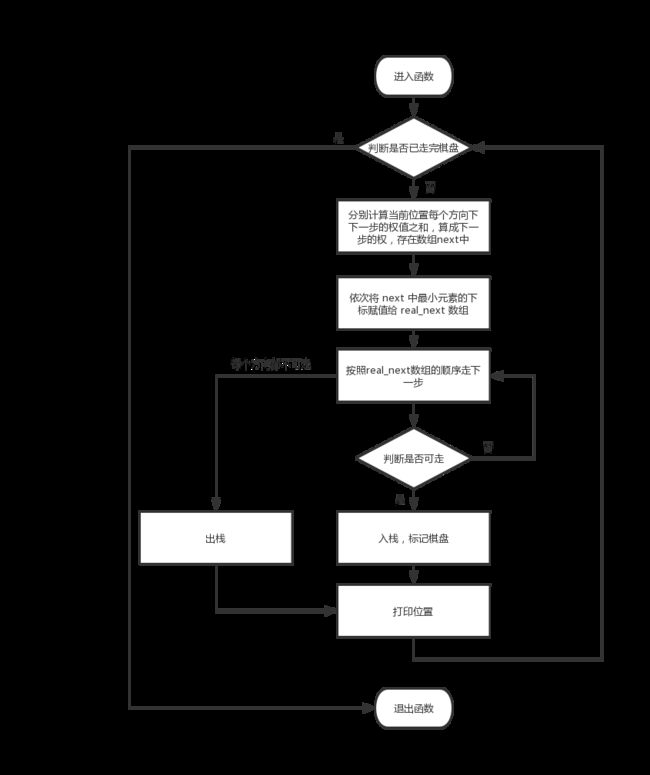
流程图
输出分析
下面环境是Linux Ubuntu 18.04
经过一系列实验输入,最终64个位置,无论是从哪个开始,都可以走完全部棋盘,且大部分情况下,没有出栈回溯的情况
以下是一号方向数组在起始位置是(1,1)所得出的答案:
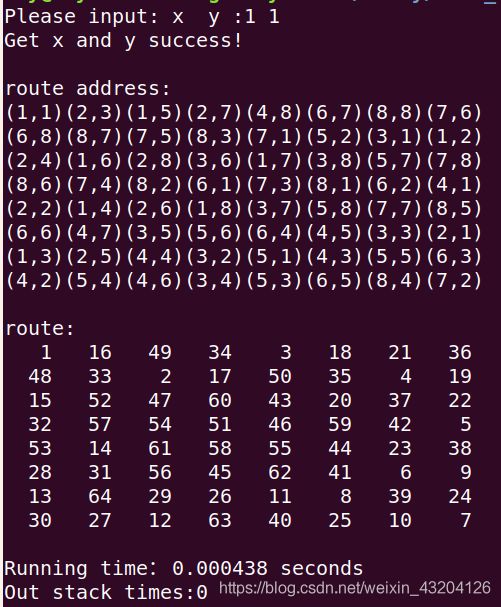
在一号方向数组中,只有在 8,6这个位置,有回溯发生:
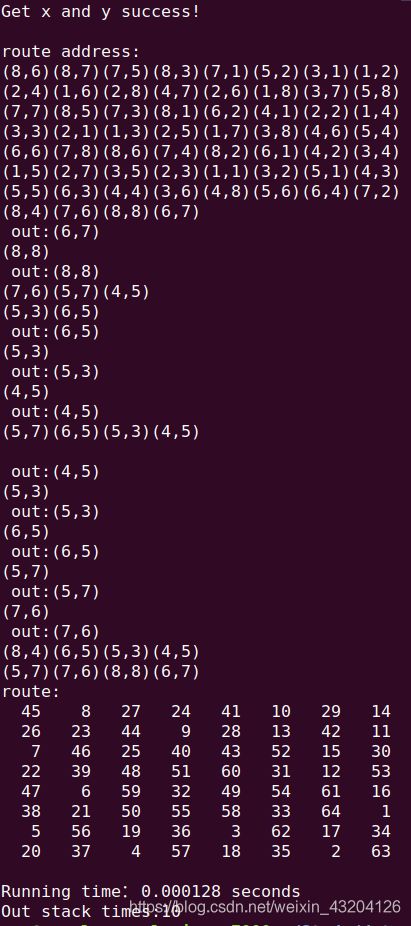
我们还应该注意的是,当方向数组的顺序定义得不同时,得到的走的方案也很大可能是不同的
下面,是二号方向数组数组的同样 (1 1)位置所得出的路径
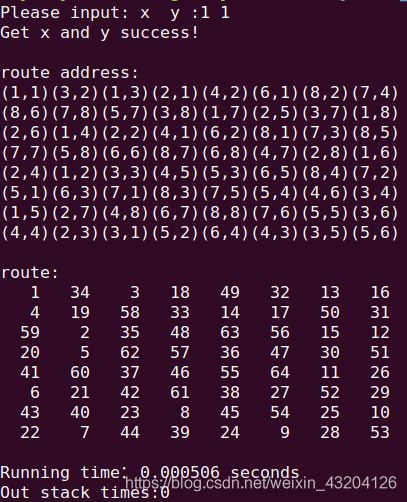
同时我们通过观察其用时发现,贪心的效率十分可观
源码
注释已加
#include暴力和简单贪心
总结至此,希望对大家可以有帮助,同时如果大家有兴趣的话,可以看一下朋友的这篇博客,里面讲解了暴力方法和简单贪心。
感谢阅读!