LeetCode第172场周赛
1323. 6 和 9 组成的最大数字
给你一个仅由数字 6 和 9 组成的正整数 num。
你最多只能翻转一位数字,将 6 变成 9,或者把 9 变成 6 。
请返回你可以得到的最大数字。
示例 1:
输入:num = 9669
输出:9969
解释:
改变第一位数字可以得到 6669 。
改变第二位数字可以得到 9969 。
改变第三位数字可以得到 9699 。
改变第四位数字可以得到 9666 。
其中最大的数字是 9969 。public class Solution {
public int maximum69Number (int num) {
String numStr = String.valueOf(num);
boolean flag = false; //未找到第一个6
StringBuilder builder = new StringBuilder();
for (int i = 0; i < numStr.length(); i++) {
char c = numStr.charAt(i);
if (!flag) {
if (c == '6') {
c = '9';
flag = true;
}
builder.append(c);
} else {
builder.append(c);
}
}
return Integer.parseInt(builder.toString());
}
}1324. 竖直打印单词
给你一个字符串 s。请你按照单词在 s 中的出现顺序将它们全部竖直返回。
单词应该以字符串列表的形式返回,必要时用空格补位,但输出尾部的空格需要删除(不允许尾随空格)。
每个单词只能放在一列上,每一列中也只能有一个单词。
示例 1:
输入:s = "HOW ARE YOU"
输出:["HAY","ORO","WEU"]
解释:每个单词都应该竖直打印。
"HAY"
"ORO"
"WEU"
示例 2:
输入:s = "TO BE OR NOT TO BE"
输出:["TBONTB","OEROOE"," T"]
解释:题目允许使用空格补位,但不允许输出末尾出现空格。
"TBONTB"
"OEROOE"
" T"这个题目的难度不大,需要注意的是如何去掉末尾的空格。这里我才用的方法是正则表达式。
public List printVertically(String s) {
String[] strs = s.split(" ");
List resList = new ArrayList<>();
int index = 0;
while(true) {
String res = "";
for (int i = 0; i < strs.length; i++) {
if (index < strs[i].length()) {
char c = strs[i].charAt(index);
res += c;
} else {
res += ' ';
}
}
index++;
if (!res.trim().isEmpty()) {
res = res.replaceAll("\\s+$",""); // 去掉末尾的空格
resList.add(res);
} else {
break;
}
}
return resList;
}
1325. 删除给定值的叶子节点
给你一棵以 root 为根的二叉树和一个整数 target ,请你删除所有值为 target 的 叶子节点 。
注意,一旦删除值为 target 的叶子节点,它的父节点就可能变成叶子节点;如果新叶子节点的值恰好也是 target ,那么这个节点也应该被删除。
也就是说,你需要重复此过程直到不能继续删除。
示例 1:
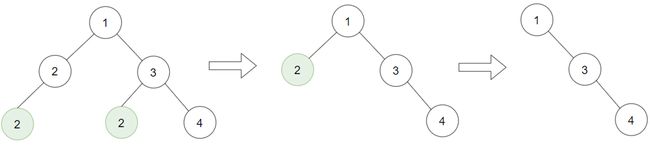
输入:root = [1,2,3,2,null,2,4], target = 2
输出:[1,null,3,null,4]对于二叉树遍历的问题首先要想到的就是递归,这道题用递归去实现非常简单,代码如下:
public TreeNode removeLeafNodes(TreeNode root, int target) {
if (root == null) {
return null;
}
root.left = removeLeafNodes(root.left, target);
root.right = removeLeafNodes(root.right, target);
if (root.left == null && root.right == null && root.val == target) {
return null;
}
return root;
}
1326. 浇灌花园的最少水龙头数目
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, ..., n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
![]()
示例 1:
输入:n = 5, ranges = [3,4,1,1,0,0]
输出:1
解释:
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
分析:
这道题是典型的动态规划问题。
对于位置为 i 的水龙头,它可以灌溉的区间为 [i - ranges[i], i + ranges[i]]。由于整个花园的区间为 [0, n],我们需要将灌溉的区间约束在 [0, n] 的范围内。我们将约束后的区间记为 [li, ri],即:
- li = max(i - ranges[i], 0)
- ri = min(i + ranges[i], n)
那么我们需要在 [l0, r0], [l1, r1], ..., [ln, rn] 中选出一些区间,使得它们可以覆盖 [0, n] 并且区间的个数最少。
dp[i] 表示把 0~i 的地都覆盖的水龙头的最少数目。在遍历 num 数组的过程中计算出这个水龙头浇灌的范围 left ~ right,那么 dp[right] = min(dp[left + 1], dp[left + 2], ......, dp[right - 1))。
public int minTaps(int n, int[] ranges) {
int[] dp = new int[n + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int i = 0; i <= n; i++) {
int left = Math.max(i - ranges[i], 0);
int right = Math.min(i + ranges[i], n);
if (dp[left] != Integer.MAX_VALUE) {
for (int j = left; j <= right; j++) {
dp[j] = Math.min(dp[j], dp[left] + 1);
}
}
}
return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];
}