python 实现RSA加密(利用OAEP填充方式)
实验目的
实现2048RSA加密并给出解密函数验证
实验原理
RSA加密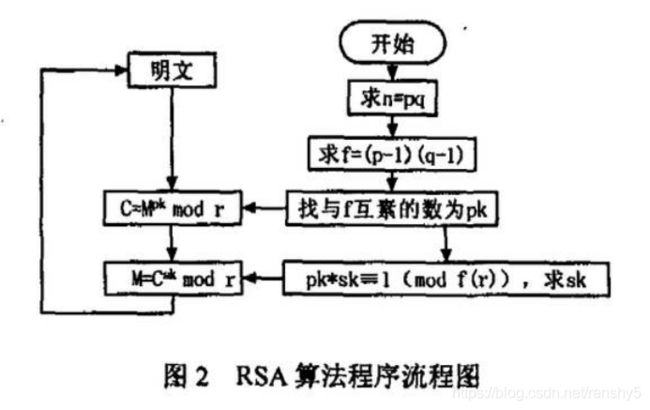
OAEP填充
实验步骤
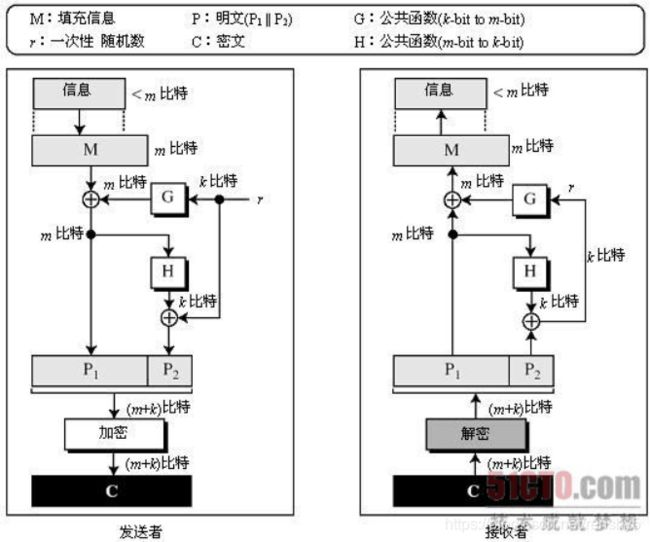
进行OAEP填充
a、把明文填充到1024bite,记为M。
b、选取一个随机数r(1024bite)。
c、把r进行G函数,此处的G函数为6次sha1,记为R。
d、把R和M进行异或得到P1。
e、把P1进行H函数,此处的H函数也为6次sha1,并和r进行异或处理得到P2。
f、把P1和P2进行合并得到OAEP填充完的字符串记为C。
进行RSA加密
a、选取两个安全素数p、q(此实验助教已给出),选取密钥a(此处的密钥是学号(17340012)的下一位素数,为17340019)。
b、计算n=pq,fn=(q-1)(p-1)。
c、计算公钥b为关于a模fn的逆。
d、私钥:(a,n),公钥(b,n)。
e、进行Y = X^b mod n。
进行RSA解密
进行X = Y^a mod n。
进行OAEP解密
a、把解密之后的C分成两部分deP1和deP2。
b、把deP1进行6次sha1操作,并把结果和deP2进行异或得到r。
c、把r进行6次sha1操作,并把结果和deP1进行异或处理得到明文M。
d、把M转化成为字符串。
实验代码
import hashlib
import random
import binascii
p = 168995677594036943498896698249502579045415356147450286903574977915675215654000852466242837180568368549600306461919095156035850147291191251838345423003548737288250427664794031697769270068290742307294644975782315875706815176748955712747679225674789516554407102487179525812178429394677953163553303283966837950227
q = 73250114511939221297189302708624091354575379476811068897570041621344734046574044427415715091676742616301137831925511472461697934230365993146217113253076136386575575868816429181422361239620593954716878229091392314316476106540409390466346705287246245765228049884691190461308813988563356306637349832642629018559
plaintext = "Sun Yat-sen University"
Pri_Key = 17340019
def gcd(a, b):
while a != 0:
a, b = b % a, a
return b
def findModReverse(a, m):
if gcd(a, m) != 1:
return None
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
q = u3 // v3
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
return u1 % m
def sha1_6times(r):
mark_r = r[2:]
x = b''
sha1 = hashlib.sha1()
for n in range(int(len(mark_r) / 2)):
b = int(mark_r[n * 2], 16) * 16 + int(mark_r[n * 2 + 1], 16)
x = x + chr(b).encode('latin1')
sha1.update(x)
mark_r = sha1.hexdigest()
P1 = mark_r
for i in range(5):
sha1 = hashlib.sha1()
sha1.update(mark_r.encode('utf-8'))
mark_r = sha1.hexdigest()
P1 = mark_r + P1
return P1
r = ""
for i in range(1024):
r += str(random.randint(0, 1))
print("the random number is(r):", r)
# to 0101010101
pad_paintext = binascii.hexlify(plaintext.encode('latin1'))
# OAEP
mark_r = str(hex(int(r, 2)))
P1 = sha1_6times(mark_r)
P1 = str(hex(int(P1, 16) ^ int(pad_paintext, 16)))
print("P1:\n", P1[2:])
mark_r = P1
P2 = sha1_6times(mark_r)
P2 = str(hex(int(P2, 16) ^ int(r, 2)))
print("P2:\n", P2[2:])
P1 = P1 + P2[2:]
print("Results after OAEP encryption:\n", P1[2:])
xx = int(P1, 16)
print("Decimal system of OAEP:\n", xx)
mul_pq = p * q
fn = (p - 1) * (q - 1)
Pub_Key = findModReverse(Pri_Key, fn)
Ey = int(pow(xx, Pub_Key, mul_pq))
print("Results after RSA encryption:\n", hex(Ey))
# decode
Ex = int(pow(Ey, Pri_Key, mul_pq))
deS = bin(Ex)
deP2 = hex(int(deS[len(deS) - 1024:], 2))
deP1 = hex(int(deS[:len(deS) - 1024], 2))
print("the deP2 is:\n", deP2)
print("the deP1 is:\n", deP1)
demark_r = deP1
demark_P1 = sha1_6times(demark_r)
demark_P2 = str(hex(int(demark_P1, 16) ^ int(deP2, 16)))
print("After decrypt the random number is(r)::\n" + demark_P2)
demark_r = demark_P2
demark_P1 = sha1_6times(demark_r)
Last_M = str(hex(int(deP1, 16) ^ int(demark_P1, 16)))
print("After decrypt plaintext is:"+binascii.a2b_hex(Last_M[2:]).decode("utf8"))实验结果
注意事项
1、p和q为大素数,在实验之前助教有直接给了我们。密钥是学号的下一位素数,这个可以使用Magma在线查找下一位素数。
输入指令:
NextPrime(number)
即可求出
2、本次实验因为是需要大数,所以直接使用python做出,其实python里面有一个库就可以直接使用RSA了!
3、我是菜鸡,就写给自己看看,如果有不足的地方,欢迎指正,但是不接受大佬的“批评”!谢谢!