OpenCV学习笔记(八)之边缘检测算子下篇(Canny算子原理及实现)
Canny 边缘检测算法 是 John F. Canny 于 1986年开发出来的一个多级边缘检测算法,此算法被很多人认为是边缘检测的最优算法,相对其他边缘检测算法来说其识别图像边缘的准确度要高很多。
最优边缘检测的三个主要评价标准是:
- 低错误率: 标识出尽可能多的实际边缘,同时尽可能的减少噪声产生的误报。
- 高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近。
- 最小响应: 图像中的边缘只能标识一次。
对Canny算子作深入剖析就会发现Canny算子对上述三个条件都能较好的满足。下面先描述下OpenCV中对Canny算子的实现函数:
//! applies Canny edge detector and produces the edge map.
CV_EXPORTS_W void Canny( InputArray image, OutputArray edges,
double threshold1, double threshold2,
int apertureSize=3, bool L2gradient=false );
其中:
4. image是输入图像,要求必须是8位单通道灰度图;
5. edges是输出图像,其是8位单通道二值化图像;
6. htreshold1是小阈值,当检测到的像素点的灰度值小于此阈值时将其标记为非边缘像素;
7. threshold2是大阈值,当检测到的像素点的灰度值大于此阈值时才标记为边缘像素;
注:当检测到的像素点的灰度值 g(x,y) > 小阈值 且 g(x,y) < 大阈值时,只有该像素点g(x,y)与边缘像素点连接(即g(x,y)为边缘像素点的邻域内的点)时才标记为边缘像素;
8. apertureSize为Sobel卷积核的内核大小,默认使用内核大小为3的卷积核;
Canny算子进行边缘检测步骤
1.转换灰度图
因为Canny算子只能对单通道灰度图像进行处理,因此在进行边缘检测之前需要将原图像进行灰度转换。openCV中已经封装好了一个函数用于转换各种格式的图像,如下:
//! converts image from one color space to another
CV_EXPORTS_W void cvtColor( InputArray src, OutputArray dst, int code, int dstCn=0 );
使用该函数可以将多通道彩色图像转换为单通道灰度图。
2.滤波降噪处理
理想中的图像信息是无噪声的,图像质量很好,但是现实中由于采集设备、环境干扰等多方面的原因导致采集到的图像信息都是含有大量噪声信息的,这些噪声最常见的就是椒盐噪声和高斯噪声;Canny算子是一种综合在抗噪声干扰和精确定位之间寻求最佳折中方案的边缘检测方法,一般使用高斯滤波来去除噪声,下面是常见的3X3的卷积核模板:
[ 1 / 16 2 / 16 1 / 16 2 / 16 4 / 16 2 / 16 1 / 16 2 / 16 1 / 16 ] \left[ \begin{matrix} 1/16 & 2/16 & 1/16 \\ 2/16 & 4/16 & 2/16 \\ 1/16 & 2/16 & 1/16 \end{matrix} \right] ⎣⎡1/162/161/162/164/162/161/162/161/16⎦⎤
高斯滤波可以将图像中的噪声部分过滤出来,避免后面进行边缘检测时将错误的噪声信息也误识别为边缘了。但是滤波核的维数不宜选的过大,否则可能会将边缘信息给平滑掉,使得边缘检测算子无法正确识别边缘信息。
3.用一阶偏导的有限差分计算梯度的幅值和方向
使用一阶有限差分计算梯度可以得到图像在x和y方向上偏导数的两个矩阵,Canny算子中使用的是 Sobel 算子作为梯度算子,当然还可以自己构造其它的如:Roberts算子、Prewitt算子等一阶边缘检测算子来作为梯度算子。下面以Sobel算子为例来计算梯度的幅值和方向:
X方向:
S x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] Sx= \left[ \begin{matrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{matrix} \right] Sx=⎣⎡−1−2−1000121⎦⎤
Y方向:
S y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] Sy= \left[ \begin{matrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{matrix} \right] Sy=⎣⎡−101−202−101⎦⎤
假设点 H ( i , j ) H{(i,j)} H(i,j)为我们要计算的图像:
H ( i , j ) = [ A 0 A 1 A 2 A 3 C A 5 A 6 A 7 A 8 ] H(i,j)= \left[ \begin{matrix} A0 & A1 & A2 \\ A3 & C & A5 \\ A6 & A7 & A8 \end{matrix} \right] H(i,j)=⎣⎡A0A3A6A1CA7A2A5A8⎦⎤
其中点 C ( i , j ) C_{(i,j)} C(i,j)为我们要计算的梯度,则:
X 方 向 梯 度 : G x = 2 × A 5 + A 2 + A 8 − ( 2 × A 3 + A 0 + A 6 ) X方向梯度: Gx = 2 \times A5+A2+A8 - (2 \times A3+A0+A6) X方向梯度:Gx=2×A5+A2+A8−(2×A3+A0+A6)
Y 方 向 梯 度 : G y = 2 × A 7 + A 6 + A 8 − ( 2 × A 1 + A 0 + A 2 ) Y方向梯度: Gy = 2 \times A7+A6+A8 - (2 \times A1+A0+A2) Y方向梯度:Gy=2×A7+A6+A8−(2×A1+A0+A2)
点 C 处 的 梯 度 幅 值 为 : G C ( i , j ) = G x 2 + G y 2 点C处的梯度幅值为: G_{C(i,j)} = \sqrt{Gx^2 + Gy^2} 点C处的梯度幅值为:GC(i,j)=Gx2+Gy2
点 C 处 的 梯 度 方 向 为 : θ = arctan ( G y / G x ) 点C处的梯度方向为: \theta = \arctan(Gy / Gx) 点C处的梯度方向为:θ=arctan(Gy/Gx)
4.非极大值抑制
什么是非极大值抑制?从字面上理解,就是对非极大值的数据进行抑制,也可以理解成对非极大值数据排除其是边缘的可能性。根据我的理解“极大值”是针对梯度来说的,8邻域内图像梯度幅值矩阵中的元素值越大,说明图像中该点的梯度值越大,再结合检测点的梯度方向,就可以定位出大概的边缘信息。
理解非极大值抑制需要知道下面两点:
- 要把当前位置的梯度值与梯度方向上两侧的梯度值进行比较;
- 梯度方向是垂直于边缘方向。
以下图为例:
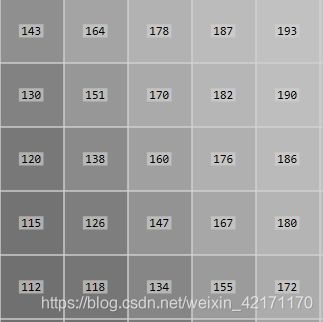
点C的 8 邻域内的每个点的X方向与Y方向梯度矩阵如下:
H ( i , j ) ( G x , G y ) = [ ( 155 , − 93 ) ( 120 , − 73 ) ( 81 , − 47 ) ( 150 , − 88 ) ( 148 , − 86 ) ( 108 , − 63 ) ( 126 , − 74 ) ( 157 , − 93 ) ( 130 , − 84 ) ] H(i,j)_{(Gx,Gy)}= \left[ \begin{matrix} (155,-93) & (120,-73) & (81,-47) \\ (150,-88) & (148,-86) & (108,-63) \\ (126,-74) & (157,-93) & (130,-84) \end{matrix} \right] H(i,j)(Gx,Gy)=⎣⎡(155,−93)(150,−88)(126,−74)(120,−73)(148,−86)(157,−93)(81,−47)(108,−63)(130,−84)⎦⎤
每个点的梯度方向的梯度角矩阵如下:
H ( i , j ) θ = [ − 31.0 − 31.1 − 30.1 − 30.4 − 30.2 − 30.3 − 30.4 − 30.6 − 32.9 ] H(i,j)_{\theta}= \left[ \begin{matrix} -31.0 & -31.1 & -30.1 \\ -30.4 & -30.2 & -30.3 \\ -30.4 & -30.6 & -32.9 \end{matrix} \right] H(i,j)θ=⎣⎡−31.0−30.4−30.4−31.1−30.2−30.6−30.1−30.3−32.9⎦⎤
OpenCV中的Canny算子将Gy/Gx的值求绝对值了,因此OpenCV中的梯度角矩阵为:
H ( i , j ) θ = [ 31.0 31.1 30.1 30.4 30.2 30.3 30.4 30.6 32.9 ] H(i,j)_{\theta}= \left[ \begin{matrix} 31.0 & 31.1 & 30.1 \\ 30.4 & 30.2 & 30.3 \\ 30.4 & 30.6 & 32.9 \end{matrix} \right] H(i,j)θ=⎣⎡31.030.430.431.130.230.630.130.332.9⎦⎤
每个点的梯度值矩阵如下:
H ( i , j ) G = [ 248 193 128 238 234 171 200 250 214 ] H(i,j)_{G}= \left[ \begin{matrix} 248 & 193 & 128 \\ 238 & 234 & 171 \\ 200 & 250 & 214 \end{matrix} \right] H(i,j)G=⎣⎡248238200193234250128171214⎦⎤
根据上面计算出来的梯度值、梯度方向可以大致判断出此 8 邻域内的值的边缘信息如下图:

使用的图像计算区域为:

可以看出,计算出来的梯度方向还是挺准确的,是沿着图像中灰度增大的部分。
因为梯度方向是同时包含多个梯度值的,因此需要将梯度方向两边的梯度值进行线性插值,插值系数β有如下要求:越靠近梯度方向的梯度值,其所占比例越大。完成非极大值抑制后,会得到一个二值图像,非边缘的点灰度值均为0,可能为边缘的点灰度值为255。这样的一个检测结果还是包含了很多由噪声及其他原因造成的假边缘,因此还需要进一步的处理,也即双阈值筛选。
5.滞后阈值
滞后阈值指的是使用双阈值来对二值化图像进行筛选,通过选取合适的大阈值与小阈值可以得出最为接近图像真实边缘的边缘图像。具体实现方法为:根据高阈值得到一个边缘图像,这样一个图像含有很少的假边缘,但是由于阈值较高,产生的图像边缘可能不闭合,为了解决这样一个问题就采用了另外一个低阈值。在高阈值图像中把边缘链接成轮廓,当到达轮廓的端点时,该算法会在断点的8邻域点中寻找满足低阈值的点,再根据此点收集新的边缘,直到整个图像边缘闭合。
以上为整个Canny边缘检测算法的原理分析,接下来进行VS2010下的算法实现和效果分析。
Canny算子源码分析
void cv::Canny( InputArray _src, OutputArray _dst,
double low_thresh, double high_thresh,
int aperture_size, bool L2gradient )
{
Mat src = _src.getMat();
CV_Assert( src.depth() == CV_8U );
_dst.create(src.size(), CV_8U);
Mat dst = _dst.getMat();
// low_thresh 表示低阈值, high_thresh表示高阈值
// aperture_size 表示卷积核算子大小,默认为3
// L2gradient计算梯度幅值的标识,默认为false,其中:
//若L2gradient = true,则计算梯度时使用如下公式G = Math.sqrt((Gx)^2 + (Gy)^2),计算出来的值更精准但是更耗时
//若L2gradient = false,则计算梯度时使用如下公式G = |Gx| + |Gy|
if (!L2gradient && (aperture_size & CV_CANNY_L2_GRADIENT) == CV_CANNY_L2_GRADIENT)
{
//backward compatibility
aperture_size &= ~CV_CANNY_L2_GRADIENT;
L2gradient = true;
}
if ((aperture_size & 1) == 0 || (aperture_size != -1 && (aperture_size < 3 || aperture_size > 7)))
CV_Error(CV_StsBadFlag, "");
if (low_thresh > high_thresh) //若低阈值 > 高阈值,则交换低阈值和高阈值
std::swap(low_thresh, high_thresh);
std::swap(low_thresh, high_thresh);
#ifdef HAVE_TEGRA_OPTIMIZATION
if (tegra::canny(src, dst, low_thresh, high_thresh, aperture_size, L2gradient))
return;
#endif
#ifdef USE_IPP_CANNY
if( aperture_size == 3 && !L2gradient &&
ippCanny(src, dst, (float)low_thresh, (float)high_thresh) )
return;
#endif
const int cn = src.channels();
Mat dx(src.rows, src.cols, CV_16SC(cn));
Mat dy(src.rows, src.cols, CV_16SC(cn));
// BORDER_REPLICATE 表示当卷积点在图像的边界时,原始图像边缘的像素会被复制,并用复制的像素扩展原始图的尺寸
// 计算x方向的sobel方向导数,计算结果存在dx中
Sobel(src, dx, CV_16S, 1, 0, aperture_size, 1, 0, cv::BORDER_REPLICATE);
Sobel(src, dy, CV_16S, 0, 1, aperture_size, 1, 0, cv::BORDER_REPLICATE);
if (L2gradient) //L2gradient为true时,对阈值进行平方操作,这样后面算梯度G时就不需要再开平方了
{
low_thresh = std::min(32767.0, low_thresh);
high_thresh = std::min(32767.0, high_thresh);
if (low_thresh > 0) low_thresh *= low_thresh;
if (high_thresh > 0) high_thresh *= high_thresh;
}
int low = cvFloor(low_thresh); //向下取整
int high = cvFloor(high_thresh);
// ptrdiff_t 是C/C++标准库中定义的一个数据类型,signed类型,通常用于存储两个指针的差(距离),可以是负数
// mapstep 用于存放
ptrdiff_t mapstep = src.cols + 2;
//这个分配空间是图像的大小(存放边缘信息)+ 3个跨度大小的容量组成一个ringbuffer(用于重复存放三排梯度值)
AutoBuffer<uchar> buffer((src.cols+2)*(src.rows+2) + cn * mapstep * 3 * sizeof(int));
int* mag_buf[3];
mag_buf[0] = (int*)(uchar*)buffer; //第一行ringbuffer
mag_buf[1] = mag_buf[0] + mapstep*cn;//第二行ringbuffer
mag_buf[2] = mag_buf[1] + mapstep*cn;//第三行ringbuffer
memset(mag_buf[0], 0, /* cn* */mapstep*sizeof(int));
uchar* map = (uchar*)(mag_buf[2] + mapstep*cn);//map用来存储图像是否是边缘的信息(值为0、1、2具体含义见下文注释)
memset(map, 1, mapstep); //给图像中最上面一行赋值为1
memset(map + mapstep*(src.rows + 1), 1, mapstep); //给图像中最下面一行赋值为1
int maxsize = std::max(1 << 10, src.cols * src.rows / 10);
std::vector<uchar*> stack(maxsize); // 定义指针类型向量,用于存地址
uchar **stack_top = &stack[0]; // 栈顶指针(指向指针的指针),指向stack[0], stack[0]也是一个指针
uchar **stack_bottom = &stack[0]; // 栈底指针 ,初始时 栈底指针 == 栈顶指针
/* sector numbers
(Top-Left Origin)
1 2 3
* * *
* * *
0*******0
* * *
* * *
3 2 1
*/
#define CANNY_PUSH(d) *(d) = uchar(2), *stack_top++ = (d) // CANNY_PUSH(d) 是入栈函数, 参数d表示地址指针,让该指针指向的内容为2(int型强制转换成uchar型),并入栈,栈顶指针+1,其中,2表示像素属于某条边缘可以看下方的注释
#define CANNY_POP(d) (d) = *--stack_top // CANNY_POP(d) 是出栈函数, 栈顶指针-1,然后将-1后的栈顶指针指向的值,赋给d
// calculate magnitude and angle of gradient, perform non-maxima suppression.
// fill the map with one of the following values:
// 0 - the pixel might belong to an edge
// 1 - the pixel can not belong to an edge
// 2 - the pixel does belong to an edge
for (int i = 0; i <= src.rows; i++)
{
//i=0时,存在mag_buf[1];i>0时存在mag_buf[2]中,后面新的梯度幅度值都放到mag_buf[2]
//循环结束前,最后一步会使ring buffer顺序循环一次,使原来mag_buf[1]中的内容放到mag_buf[0]
//mag_buf[2]放到mag_buf[1]中,原来mag_buf[0]中的内容就被覆盖掉
int* _norm = mag_buf[(i > 0) + 1] + 1; //跳过第一列,指向原始图像每一行的第一个点
if (i < src.rows)
{
short* _dx = dx.ptr<short>(i); // _dx指向dx矩阵的第i行
short* _dy = dy.ptr<short>(i);
if (!L2gradient)
{//当L2gradient为 false 时,粗略计算梯度值G = |Gx| + |Gy|
for (int j = 0; j < src.cols*cn; j++)
_norm[j] = std::abs(int(_dx[j])) + std::abs(int(_dy[j]));
}
else
{
//精确计算梯度值G = Math.sqrt((Gx)^2 + (Gy)^2),由于高低阈值都被平方了,所以此处_norm[j]无需开平方
for (int j = 0; j < src.cols*cn; j++)
_norm[j] = int(_dx[j])*_dx[j] + int(_dy[j])*_dy[j];
}
if (cn > 1) //如果不是单通道
{
for(int j = 0, jn = 0; j < src.cols; ++j, jn += cn)
{
int maxIdx = jn;
for(int k = 1; k < cn; ++k)
if(_norm[jn + k] > _norm[maxIdx]) maxIdx = jn + k;
_norm[j] = _norm[maxIdx];
_dx[j] = _dx[maxIdx];
_dy[j] = _dy[maxIdx];
}
}
_norm[-1] = _norm[src.cols] = 0; //第一列和最后一列不可能是边缘,梯度设为0
}
else
// 当i == src.rows(最后一行)时,存储在mag_buf[2]中,并且初始化其中的值为0
memset(_norm-1, 0, /* cn* */mapstep*sizeof(int));
// at the very beginning we do not have a complete ring
// buffer of 3 magnitude rows for non-maxima suppression
//满足非极大值限制,只能推出该点可能为边缘点
//这里要满足两个条件,如果是梯度在邻域中是最大值,且大于high阈值,确定是边缘点,然后以此为中心需找邻域中满足低阈值的点
if (i == 0)
continue;
uchar* _map = map + mapstep*i + 1; //暂时存处当前行的地址,+1表示排除扩充的第一列
_map[-1] = _map[src.cols] = 1; //第一列和最后一列赋值为1表示不可能是边缘
int* _mag = mag_buf[1] + 1; // take the central row
ptrdiff_t magstep1 = mag_buf[2] - mag_buf[1]; //负数 用于向下跳转一行
ptrdiff_t magstep2 = mag_buf[0] - mag_buf[1]; //负数 用于向上跳转一行
//x方向梯度值指针指向上一行,这里之所以是i-1是因为图像是从i=1开始计算的,也就是图像第一行对应着i=1,原因是:for (int i = 0; i <= src.rows; i++)
const short* _x = dx.ptr<short>(i-1);
const short* _y = dy.ptr<short>(i-1);
if ((stack_top - stack_bottom) + src.cols > maxsize) //当存不下时,给stack扩容
{
int sz = (int)(stack_top - stack_bottom);
maxsize = maxsize * 3/2;
stack.resize(maxsize);
stack_bottom = &stack[0];
stack_top = stack_bottom + sz;
}
int prev_flag = 0; //为1代表前一个像素点为边缘点,为0代表前一个点为非边缘点
for (int j = 0; j < src.cols; j++)
{
#define CANNY_SHIFT 15
const int TG22 = (int)(0.4142135623730950488016887242097*(1<<CANNY_SHIFT) + 0.5);
int m = _mag[j]; //_mag = mag_buf[1] + 1 读出上一行j列的梯度值
if (m > low) // 如果大于低阈值
{
int xs = _x[j]; // dx中 第i-1行 第j列
int ys = _y[j];
int x = std::abs(xs);
int y = std::abs(ys) << CANNY_SHIFT;
int tg22x = x * TG22;
if (y < tg22x) //当前行j列处的梯度值的角度小于22.5度时,比较当前行j列左右两个点的值(m点的8邻域内左右两点)
{
if (m > _mag[j-1] && m >= _mag[j+1]) goto __ocv_canny_push; //满足条件跳转再判断是边缘点2,还是不确定边缘点0
}
else
{
int tg67x = tg22x + (x << (CANNY_SHIFT+1));
//当前行j列处的梯度值的角度大于67.5度时,比较当前行j列前一行j列与后一行j列两个点的值(m点的8邻域内上下两点)
if (y > tg67x)
{
if (m > _mag[j+magstep2] && m >= _mag[j+magstep1]) goto __ocv_canny_push;
}
//当前行j列处的梯度值的角度处于【22.5,67.5】之间时,比较当前行j列前一行j列与后一行j列两个点的值(m点的8邻域内斜对角两点)
else
{
//按位异或,用于判断符号是否相同,不同就为-1,比较对角线上两个点的值,当s=-1时,比较(/)这种斜对角,当s=1时,比较(\)这种斜对角
int s = (xs ^ ys) < 0 ? -1 : 1;
if (m > _mag[j+magstep2-s] && m > _mag[j+magstep1+s]) goto __ocv_canny_push;
}
}
}
prev_flag = 0;
_map[j] = uchar(1);
continue;
__ocv_canny_push:
//前一个点不是边缘点,并且当前点的值大于high阈值,并且正对上一行那个点也不是边缘点,那么该点为边缘点
//说白了就是领域最大值才有资格先成为边缘点
if (!prev_flag && m > high && _map[j-mapstep] != 2)
{
CANNY_PUSH(_map + j);
prev_flag = 1;
}
else
_map[j] = 0;
}
//循环结束前,使ring buffer顺序循环一次,使原来mag_buf[1]中的内容放到mag_buf[0]
//mag_buf[2]放到mag_buf[1]中,原来mag_buf[0]中的内容就被覆盖掉
// scroll the ring buffer
_mag = mag_buf[0];
mag_buf[0] = mag_buf[1];
mag_buf[1] = mag_buf[2];
mag_buf[2] = _mag;
}
// 通过上面的for循环,确定了各个邻域内的极大值点为边缘点(标记为2)
// 现在,在这些边缘点的8邻域内(上下左右+4个对角),将可能的边缘点(标记为0)确定为边缘
// now track the edges (hysteresis thresholding)
while (stack_top > stack_bottom)
{
uchar* m;
if ((stack_top - stack_bottom) + 8 > maxsize) //扩容
{
int sz = (int)(stack_top - stack_bottom);
maxsize = maxsize * 3/2;
stack.resize(maxsize);
stack_bottom = &stack[0];
stack_top = stack_bottom + sz;
}
CANNY_POP(m); //pop出边缘地址
//下面几段将m周围8领域内的原来是0的点(可能是边缘点的点)改为边缘点
//m[-mapstep-1] m[-mapstep] m[-mapstep+1]
//m[-1] m[0] m[1]
//m[mapstep-1] m[mapstep] m[mapstep+1]
if (!m[-1]) CANNY_PUSH(m - 1);
if (!m[1]) CANNY_PUSH(m + 1);
if (!m[-mapstep-1]) CANNY_PUSH(m - mapstep - 1);
if (!m[-mapstep]) CANNY_PUSH(m - mapstep);
if (!m[-mapstep+1]) CANNY_PUSH(m - mapstep + 1);
if (!m[mapstep-1]) CANNY_PUSH(m + mapstep - 1);
if (!m[mapstep]) CANNY_PUSH(m + mapstep);
if (!m[mapstep+1]) CANNY_PUSH(m + mapstep + 1);
}
//画出边缘图像
// the final pass, form the final image
const uchar* pmap = map + mapstep + 1;
uchar* pdst = dst.ptr();
for (int i = 0; i < src.rows; i++, pmap += mapstep, pdst += dst.step)
{
for (int j = 0; j < src.cols; j++)
pdst[j] = (uchar)-(pmap[j] >> 1);
}
}
从源码可以看出,Canny算子不仅可以计算单通道的图像,也可以计算多通道的图像。但是,不管是单通道还是多通道都有个前提,就是输入的源图像必须是CV_8U类型的,也就是说输入图像必须是8位的,canny才能处理。不过一般我们在做Canny运算之前都会做灰度转换、滤波等操作,因此输入Canny函数中计算的源图像就是单通道灰度图。由于工作原因,这篇博客前前后后写了大概半个月才做完对OpenCV中源码的分析,不过收获还是相当大的,通过阅读源码,加深了我对OpenCV中Canny算子的原理及实现方法,这样的好处就是以后再使用canny算子时会更加得心应手。