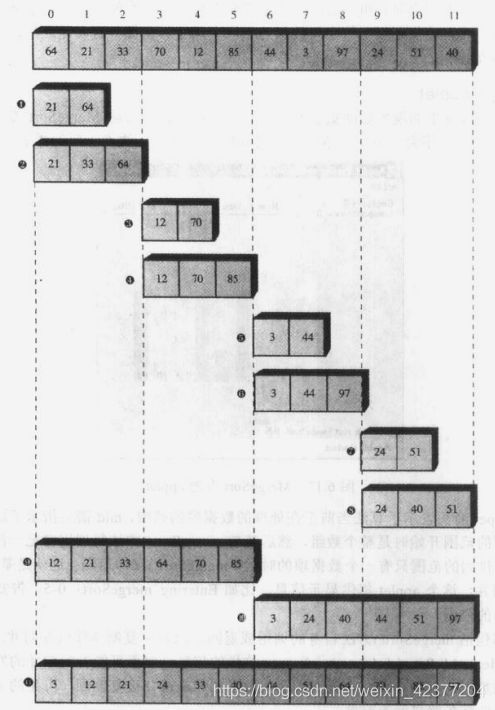
Java实现归并排序算法

     个人看法，归并，就是通过递归的方法将数组合并以实现排序的功能。
     首先我们拿最简单的一个数组作为例子【3，2，1】。
     我们通过递归将这个数组平分，然后再将平分之后的数组合并。我们处理合并的时候，会调用一个可以将两个有序数组合并为一个有序数组的方法。
     平分（递）：
     【3，2，1】->【【3，2】【1】】->【【【3】【2】】【1】】
     当数组不可再分之后，这时这个数组就是有序的了。例【3】、【2】和【1】
     合并（归）：
     【【【3】【2】】【1】】->【【2，3】【1】】->【1，2，3】
     当然，我们不必真的将一个数组平分后，装在两块内存空间内，我们只需给出平分数组的下标即可。
递归核心代码：

	private void sort(int lower, int upper) {
        if (lower == upper)
            return;
        else {
            int mid = (lower + upper) / 2;
            sort(lower, mid);
            sort(mid + 1, upper);
            merge(lower, upper);
        }
    }

     除了上面这个函数，用以实现合并的函数也比较重要，但也很容易实现。如下：

    /**
     * 将一个前后半部分局部有序的数组整理为整个数组有序
     * @param lower 数组第一个元素的下标
     * @param upper 数组最后一个元素的下标
     */
    private void merge(int lower, int upper) {
        System.out.println("lower = " + lower + ", upper = " + upper);
        int workTemp_size = upper - lower + 1;
        long[] temp = new long[workTemp_size];
    	// 将要处理的数据复制到数组 temp 中
    	for (int i = lower; i <= upper; i++)
        temp[i - lower] = theArr[i];

    	//  将 temp 中前后两部分局部有序的数组整理到 theArray 中
    	int front_lower = 0;
    	int front_upper = (workTemp_size - 1) / 2;
    	int rear_lower = front_upper + 1;
    	int rear_upper = workTemp_size - 1;
    	while (front_lower <= front_upper && rear_lower <= rear_upper) {
        if (temp[front_lower] < temp[rear_lower])
            theArr[lower++] = temp[front_lower++];
        else
            theArr[lower++] = temp[rear_lower++];
    	}

    	while (front_lower <= front_upper)
        	theArr[lower++] = temp[front_lower++];
    	while (rear_lower <= rear_upper)
        	theArr[lower++] = temp[rear_lower++];

    	System.out.println(Arrays.toString(theArr));
    	System.out.println();
	}

     该函数有两个参数，这两个参数都用于描述要进行合并的数组，lower 是数组第一个元素下标，upper 是数组最后一个元素的下标。因为调用该函数的上一步，已经将数组中【lower，mid】和【mid+1，upper】 两部分都处理为有序，mid = (lower + upper)/2。所以该函数只需要将这两部分局部有序的数据整理为整体有序即可。上面的做法是按原序复制原数组中下标在【lower，upper】内的数据到一个新的数组 temp 中。然后再通过在 temp 中对两部分局部有序的数据进行比较，将最终整体有序的数据输入到原数组的【lower，upper】位置内。
     这里有一点需要特别注意，对于中点的取值，在递归函数里和在合并函数里一点要一致。否则，将会导致运行结果不符合排序要求。
     下面将给出整体的归并排序算法的实现过程和运行结果，结合运行结果可以更加直观地理解该算法的思想和实现过程。

public class MergeSort {

    private long[] theArr;
	private int size;

	public MergeSort(long[] arr) {
        size = arr.length;
        theArr = new long[size];
        this.theArr = arr;
    }

    /**
     * 将一个前后半部分局部有序的数组整理为整个数组有序
     * @param lower 数组第一个元素的下标
     * @param upper 数组最后一个元素的下标
     */
    private void merge(int lower, int upper) {
        System.out.println("lower = " + lower + ", upper = " + upper);
        int workTemp_size = upper - lower + 1;
        long[] temp = new long[workTemp_size];

        // 将要处理的数据复制到数组 temp 中
        for (int i = lower; i <= upper; i++)
            temp[i - lower] = theArr[i];

        //  开始将 temp 中前后两部分局部有序的数组整理到 theArray 中
        int front_lower = 0;
        int front_upper = (workTemp_size - 1) / 2;
        int rear_lower = front_upper + 1;
        int rear_upper = workTemp_size - 1;
        while (front_lower <= front_upper && rear_lower <= rear_upper) {
            if (temp[front_lower] < temp[rear_lower])
                theArr[lower++] = temp[front_lower++];
            else
                theArr[lower++] = temp[rear_lower++];
        }
        while (front_lower <= front_upper)
            theArr[lower++] = temp[front_lower++];
        while (rear_lower <= rear_upper)
            theArr[lower++] = temp[rear_lower++];

        System.out.println(Arrays.toString(theArr));
        System.out.println();
    }

    private void sort(int lower, int upper) {
        if (lower == upper)
            return;
        else {
            int mid = (lower + upper) / 2;
            sort(lower, mid);
            sort(mid + 1, upper);
            merge(lower, upper);
        }
    }
    
    private void display() {
        System.out.println(Arrays.toString(theArr));
    }

    public static void main(String[] args) {
        long[] arr = new long[]{64, 21, 33, 70, 12, 85, 44, 3, 99, 0, 108, 36};
        MergeSort mergeSort = new MergeSort(arr);
        System.out.println("初始数组");
        mergeSort.display();
        System.out.println();
        mergeSort.sort(0, arr.length - 1);
    }
}

运行结果：

初始数组
[64, 21, 33, 70, 12, 85, 44, 3, 99, 0, 108, 36]

lower = 0, upper = 1
[21, 64, 33, 70, 12, 85, 44, 3, 99, 0, 108, 36]

lower = 0, upper = 2
[21, 33, 64, 70, 12, 85, 44, 3, 99, 0, 108, 36]

lower = 3, upper = 4
[21, 33, 64, 12, 70, 85, 44, 3, 99, 0, 108, 36]

lower = 3, upper = 5
[21, 33, 64, 12, 70, 85, 44, 3, 99, 0, 108, 36]

lower = 0, upper = 5
[12, 21, 33, 64, 70, 85, 44, 3, 99, 0, 108, 36]

lower = 6, upper = 7
[12, 21, 33, 64, 70, 85, 3, 44, 99, 0, 108, 36]

lower = 6, upper = 8
[12, 21, 33, 64, 70, 85, 3, 44, 99, 0, 108, 36]

lower = 9, upper = 10
[12, 21, 33, 64, 70, 85, 3, 44, 99, 0, 108, 36]

lower = 9, upper = 11
[12, 21, 33, 64, 70, 85, 3, 44, 99, 0, 36, 108]

lower = 6, upper = 11
[12, 21, 33, 64, 70, 85, 0, 3, 36, 44, 99, 108]

lower = 0, upper = 11
[0, 3, 12, 21, 33, 36, 44, 64, 70, 85, 99, 108]

接下来，配多一张来自《Java 数据结构和算法》的配图：