《Graph U-Nets》阅读笔记
1.g-U-Nets框架
作者将图像分割领域的unte模型进行迁移,通过重新定义图池化和图池化样,将unet框架迁移到图节点分类领域。
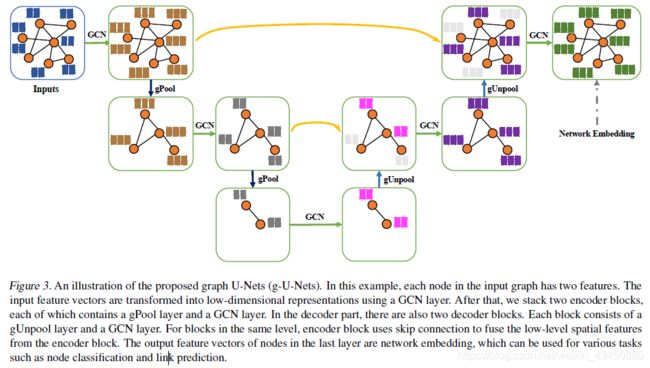
2.图池化层
1.设置可学习参数 p ∈ R F p\in R^F p∈RF, F F F表示节点的特征维度,通过向量 p p p将节点特征映射为一个标量,
y = X l p l / ∣ ∣ p l ∣ ∣ (1) y = X^lp^l/||p^l||\tag1 y=Xlpl/∣∣pl∣∣(1)
其中, X l X^l Xl为图的节点特征, y y y为映射得到的标量构成的向量。
2.选出最大的前k个值对应的节点特征:
i d x = r a n k ( y , k ) (2) idx=rank(y,k)\tag{2} idx=rank(y,k)(2)
y ~ = s i g m o i d ( y ( i d x ) ) (3) \tilde y=sigmoid(y(idx))\tag{3} y~=sigmoid(y(idx))(3)
X ~ l = X l ( i d x , : ) (4) \tilde X^l=X^l(idx,:)\tag{4} X~l=Xl(idx,:)(4)
其中, r a n k ( ∗ ) rank(*) rank(∗)表示对 y y y排序并返回最大的前 k k k个值所对应的节点索引, 式(3)表示将前 k k k个 y y y值取出,构成 y ~ \tilde y y~并进行非线性激活。
3. 利用 X ~ l \tilde X^l X~l与 y ~ \tilde y y~逐点相乘,达到选择性保留关键节点信息的目的:
X l + 1 = X ~ l ⨀ y ~ (5) X^{l+1}=\tilde X^l \bigodot \tilde y\tag5 Xl+1=X~l⨀y~(5)
4.在得到最大的前 k k k个值所对应的节点索引 i d x idx idx后,对应索引节点构成子图,从原始的图中得到相应的子图结构:
A l + 1 = A l ( i d x , i d x ) (6) A^{l+1}=A^l(idx,idx)\tag6 Al+1=Al(idx,idx)(6)
但是,在图池化时,由于只取出关键节点,把其他节点除去,可能会造成孤立节点的存在。所以在使用图卷积时,将邻接矩阵选择为:
A 2 = A l A l , A l + 1 = A 2 ( i d x , i d x ) (7) A^2=A^lA^l,A^{l+1}=A^2(idx,idx)\tag7 A2=AlAl,Al+1=A2(idx,idx)(7)
使用 A A A的次幂作为邻接矩阵,将增强节点之间的连接性, A 2 A^2 A2表示hop为2的连接关系,相当于增加了卷积时的感受野。
3.图上池化层
图上池化层中,作者在图中直接插值 0 0 0元,在相应池化层时,记录下选择节点的索引 i d x idx idx,构建 N × C N \times C N×C的全 0 0 0矩阵,并将对应索引的 k k k个节点的特征值替换全0矩阵中相应位置的 k k k个节点的值:
X l + 1 = d i s t r i b u t e ( 0 N × C , X l , i d x ) (8) X^{l+1}=distribute(0_{N \times C},X^l,idx)\tag8 Xl+1=distribute(0N×C,Xl,idx)(8)
其中, d i s t r i b u t e ( ∗ ) distribute(*) distribute(∗)表示将 X l X^l Xl按照 i d x idx idx的索引替换 0 N × C 0_{N \times C} 0N×C的相应位置。
4.改进图卷积
在图卷积公式中:
X l + 1 = σ ( D ^ − 1 / 2 A ^ D ^ − 1 / 2 X l W l ) (9) X_{l+1}=\sigma(\hat D^{-1/2}\hat A \hat D^{-1/2}X_lW_l)\tag9 Xl+1=σ(D^−1/2A^D^−1/2XlWl)(9)
A ^ = A + I \hat A=A+I A^=A+I,通过在邻接矩阵 A A A中加上单位阵 I I I保证中心节点对更新后节点的值有影响,作者希望中心节点在更新时,自身的值对更新后的值有更大的影响,所以:
A ^ = A + 2 I 0 (1) \hat A =A+2I\tag10 A^=A+2I0(1)
