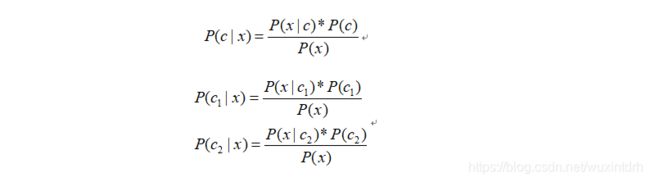朴素贝叶斯决策(Naive Bayes)
一、贝叶斯决策理论
1.1、贝叶斯公式推导
二、逻辑实现
2.1、问题引入
垃圾邮件分类:
- 样本:10000封邮件,每个邮件被标记为垃圾邮件或者非垃圾邮件
- 分类目标:给定第10001封邮件,确定它是垃圾邮件还是非垃圾邮件。 未标记
类别c:垃圾邮件c1,非垃圾邮件c2
2.2、已有公式 贝叶斯公式
2.3、问题分析
三、实例
3.1、网站留言板有如下6条留言
0 ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
1 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
0 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
1 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
0 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
1 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
1代表侮辱性言论,0代表正常言论
3.2、统一文本形式
每个文本有统一形式利于判断。通常将文本转换为词向量(VSM向量空间模型)。
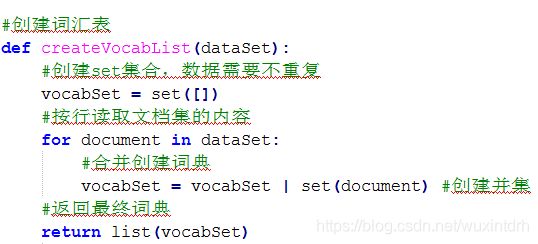
3.2.1、构建词汇表
根据已有数据,对单词进行去重。去重后含有不重复单词32个。
[my, dog, has, flea, problems, help, please, maybe, not, take, him, to, park, stupid, dalmation, is, so, cute, I, love, stop, posting, worthless, garbage, mr, licks, ate, steak, how, quit, buying, food]
3.2.2、文本表示
词集模型
[‘my’, ‘dog’, ‘has’, ‘flea’, ‘problems’, ‘help’, ‘please’]
可以用如下方式表示,对照词汇表,出现的单词标记为1,不出现记为0。
[1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
任意一篇文档可以用上述方式进行表示。
def setOfWords2Vec(vocabList, inputSet):
'''
基于贝努利模型: 只考虑词在文档中出现与否, 假设词是等权重的
生成词汇向量
:param vocabList: 词汇列表
:param inputSet: 某个文档
:return: 文档向量
'''
# 创建一个和词汇列表等长的向量
returnVec = [0] * len(vocabList)
# 将输入数据集映射到相应位置
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec
词袋模型
词集模型只标识了单词在一篇文档中是否出现,我们也可以用单词在文档中出现的次数表示,这种表示方法称作词袋模型。
def bagOfWords2VecMN(vocabList, inputSet):
'''
词袋模型:每个单词可以出现多次
:param vocabList: 词汇列表
:param inputSet: 文档
:return: 词汇向量
'''
returnVec = [0] * len(vocabList)
for word in inputSet:
if word in vocabList:
# 注意此处与词集模型的区别: 记录每个单词出现的次数, 而不是出现与否
returnVec[vocabList.index(word)] += 1
return returnVec
3.2.3、先验概率
3.2.4、类条件概率
3.2.4.1、正常言论中, 出现dog的概率
3.2.4.2、侮辱性言论中, 出现dog的概率
3.2.4、存在的问题
问题一:下溢出
问题二:概率为0
3.3、代码实现
3.3.1、创建样本
3.3.2、创建词汇表
3.3.3、根据词汇表,将句子转化为向量
3.3.4、贝叶斯实现
3.3.4.1、伪代码
计算每个类别中的文档数目
对每篇训练文档:
对每个类别: // c1 c2
如果词条出现在文档中→增加该词条的计数值
增加所有词条的计数值
对每个类别:
对每个词条:
将该词条的数目除以总词条数目得到类条件概率
返回每个类别的条件概率
代码实现
# 贝叶斯实现
def trainNB0(trainMatrix, trainCategory):
'''
:param trainMatrix: · 输入文档的词向量
:param trainCategory: 输入文档的分类
:return:
'''
numTrainDocs = len(trainMatrix) # 文档数量
numWords = len(trainMatrix[0]) # 词汇表的长度
# 侮辱性的概率, pAb代表的是分类为1的文件占所有文件的比例,也就是先验概率
pAbusive = sum(trainCategory)/float(numTrainDocs)
# 此处 为了解决可能出现概率为0, 修正公式, 拉普拉斯平滑
p0Num = ones(numWords); p1Num = ones(numWords)
p0Denom = 2.0;
p1Denom = 2.0
# 对每篇文档
for i in range(numTrainDocs):
# 对每个分类
if trainCategory[i] == 1:
p1Num += trainMatrix[i] ## 增加该词条的计数值
p1Denom += sum(trainMatrix[i]) ## 增加所有词条的计数值
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
## 计算 类条件概率
## 为了解决多个小数乘积, 数据越来越小, 取对数
# p0V代表0分类下,每个单词的出现概率,也就是类条件概率(由于用了log,所以是负数,并且由于+1,故没有无穷大项目)
# p1V代表1分类下,每个单词的出现概率
p1Vect = log(p1Num / p1Denom)
p0Vect = log(p0Num / p0Denom)
return p0Vect,p1Vect,pAbusive
3.3.4.2、根据先验概率, 类条件概率, 计算哪一类的概率比较大, 判定为那类
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
'''
:param vec2Classify: 测试文档向量
:param p0Vec: 在非侮辱性文档中, 词汇表的单词的概率
:param p1Vec:
:param pClass1: 侮辱性的先验概率
:return:
'''
# 在对数空间中进行
p1 = sum(vec2Classify * p1Vec) + log(pClass1)
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
测试
def testingNB():
# 加载数据
listOPosts,listClasses = loadDataSet()
# 创建词汇表
myVocabList = createVocabList(listOPosts)
trainMat=[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
# 测试文档
testEntry = ['love', 'my', 'dalmation']
# 对应的文档词汇向量
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
testEntry = ['stupid', 'garbage']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
## 测试
if __name__ == "__main__":
testingNB()