本文作者Key,博客园主页:https://home.cnblogs.com/u/key1994/
本内容为个人原创作品,转载请注明出处或联系:[email protected]
今天学习了决策树的分类原理,总体来说理解决策树要比理解SVM简单的多,原因有二:
(1) 决策树的分类思想与人类的思考模式更为相似——即分而治之。
(2) 决策树在实现时规则非常固定,模式非常单一,降低了其理解难度。
但是,决策树在选择最优划分属性时引入了熵(Entropy)和信息增益(Information Gain)的概念,理解起来比较抽象,因此本文将采用简单的例子来加深理解。
上图是本文使用的简易模型,将该模型数据整理到表格中:
| x |
y |
class |
x |
y |
class |
| 1 |
1 |
cir |
3 |
4 |
tan |
| 1 |
2 |
cir |
3 |
5 |
tan |
| 1 |
3 |
cir |
3 |
6 |
tan |
| 1 |
4 |
tan |
4 |
1 |
cir |
| 1 |
5 |
tan |
4 |
2 |
tri |
| 1 |
6 |
tan |
4 |
3 |
tri |
| 2 |
1 |
cir |
4 |
4 |
tri |
| 2 |
2 |
cir |
4 |
5 |
tri |
| 2 |
3 |
cir |
4 |
6 |
tri |
| 2 |
4 |
tan |
5 |
1 |
cir |
| 2 |
5 |
tan |
5 |
2 |
tri |
| 2 |
6 |
tan |
5 |
3 |
tri |
| 3 |
1 |
cir |
5 |
4 |
tri |
| 3 |
2 |
cir |
5 |
5 |
tri |
| 3 |
3 |
cir |
5 |
6 |
tri |
很明显,在建立决策树模型时,有两种思路:
(1) 先按照x坐标分类,然后按照y坐标分类;
(2) 先按照y坐标分类,然后按照x坐标分类。
至于选择哪一种方案更好,可以根据决策树的相关理论,分别求出信息增益。
但是,这里我有一个疑问,假如我们选择方案(1),即先按照x坐标来分类。很明显,所有样本的类别有三类,但是x的取值有5个(分别为1,2,3,4,5)。按照决策树理论,应该选择如下方式:
根据样本数据的分布规律可以看出,如果采用如下方式效率更高:
但是,这种分类方法不具有一般性,毕竟不是所有问题都能够通过肉眼观察出规律,我们要做的是让机器自己来决策。Anyway,在这里我们暂且将该问题搁置不管,因为本文讨论的内容是熵与信息增益的实质。
接下来,才是本文的核心内容。
比较上面提出的两种方案,我们很难认为分辨出其好坏。下面我们分别求出信息增益。
方案(1):
首先按照x坐标来分类。
分别计算各个节点的熵:(计算过程省略)
Entropy(parent)=1.58
Entropy(children1)=1
Entropy(children2)=0.65
IG=0.72
方案(2):
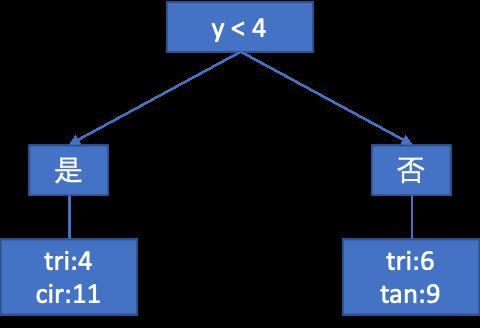
首先按照y坐标来分类。
分别计算各个节点的熵:(计算过程省略)
Entropy(parent)=1.58
Entropy(children1)=0.8367
Entropy(children2)=0.971
IG=0.8067
从信息增益的值来看,应该选择第二种方案来进行分类。但是如果选择第二种方案,最终的得到的分类器的分类精度将会低于第一种方案(该论述非常容易证明,读者可以自行计算)。也就是说,从分类器的精度来评判,第二种方案效果更差。那么为什么会出现这种现象呢?
这里我们要从原理上来分析。
什么是熵,从定义上来看,熵的值表征着样本集合中的纯度(purity)大小。如果所有样本只有一个类别,那么此时的纯度非常高,通过计算得到的熵值为0;而如果样本有多个类别,纯度会变低,熵值也会随之增大。最特殊的情况,就是在所有样本中,每种类别的数量均相等,此时熵值为1,纯度最低。
而信息增益的计算公式为父节点的熵值减各子节点的熵值的加权和,即按照当前属性来划分时由父节点到子节点的纯度变化值。信息增益的值一定不小于零,因为经过划分之后各子节点的纯度一定是越来越高的,即各子节点的熵值一定是在变小的,即使加权求和之后还是会小于父节点的熵值。此外,信息增益值越大,说明纯度提高越明显。我们当然希望纯度提高速度快一点,那样我们就能以最快的速度来完成分类器的训练。
这里要注意,根据信息增益的大小来确定划分属性时,我们主要考虑的是分类亲训练的速度,而非精度,这也解释了为什么在以上的示例中,方案二的精度会低于方案一。
看上去这是一个bug,那为什么信息增益理论如此受追捧呢?我们大胆的猜想一下,在实际问题中,一个模型的属性有可能有多个,假如说有10个,而每个属性可取值3个,这样的话我们的模型会非常复杂,计算量也会大增。而实际的问题的复杂程度有可能比我的假设有过之无不及。所以,我们必须要考虑计算速度的问题,即使需要以损失部分精度为代价。而这在机器学习问题中是非常常见的——即寻求计算量与精度的平衡!
此外,如果我们每个样本点都不想错误分类,那么如何来避免overfitting呢?
既然讲到决策树,那就顺便说一下我对决策树算法的一些理解。如有不准确的地方,希望各位读者批评指正。
首先,虽然决策树可以用于回归,但是其主要应用还是进行分类;
其次,使用决策树算法时,若想取得好的分类效果,一定是以大数据为前提的。只有数据量足够大,决策树才能够便利各种可能出现的情况。而大量的数据又会给训练带来挑战;
最后,决策树的参数选取也是一个复杂的过程。前面已经证明了基于信息增益来选择最优划分属性的方法可能无法取的较好的训练效果。若想提高决策树的分类精度,还有很多参数需要提前确定,比如criterion(entropy/gini)、spllitter(random/best)、max_depth(决策树的深度)、min_samples_split(最小分类样本数)等等,这些参数的选取过程比较复杂。