基于python实现遗传算法
一、研究背景
- 求解最优化问题的方法主要包括遗传算法、粒子群算法、蚁群算法等。与传统的搜索算法(牛顿法、斐波那契法、二分法等)相比,这三种算法具有高鲁棒性和求解高度复杂的非线性问题 的能力。本文主要针对遗传算法做出介绍和讲解。
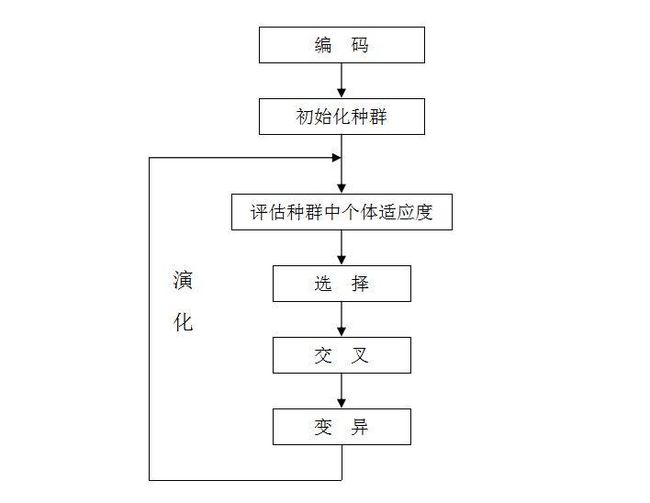
- 遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此,在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。(来源:百度百科)
- 简而言之,遗传算法便是基于达尔文的进化论,模拟自然选择,物竞天择、适者生存,通过N代的遗传、变异、交叉、复制,进化出问题的最优解。
- Geatpy是python中最常用到的遗传算法类库,包括了编码、适应度计算、选择、重组、变异、重插入、多目标优化等方面的一些方法,同时,该类库也内置了一些经典算法,可以直接使用,内置的算法包括:
单目标算法:
- 基于多种群竞争进化单目标编程模板(实值编码)
- 基于多种群独立进化单目标编程模板(实值编码)
- 改进的单目标编程模板(二进制/格雷编码)
- 改进的单目标编程模板(排列编码)
- 改进的单目标编程模板(实值编码)
- 单目标编程模板(排列编码)
- 单目标编程模板(实值编码)
- 单目标编程模板(二进制/格雷编码)
多目标算法:
- 基于适应性权重法(awGA)的多目标优化的进化算法模板
- 基于改进NSGA-Ⅱ算法求解多目标优化问题的进化算法模板
- 基于改进的快速非支配排序法求解多目标优化问题的进化算法模板
- 基于快速非支配排序法求解多目标优化问题的进化算法模板
- 基于随机权重法(rwGA)的多目标优化的进化算法模板
多种算法的输入输出变量相近,可以很方便的调用对比,也可以根据内置的方法编写自己的遗传算法。
二、内核函数介绍
图中黑色的表示 Geatpy 中内置的函数 (当然用户也可以自定义与之类似的函数);红色的表示是用户自定义的。其中, templet* 是进化算法模板, * 表示名字是多样的;aimfunc* 是优化目标函数; crt* 用于创建种群染色体矩阵 (简称“种群矩阵” ); bs2* 用于二进制/格雷码种群的解码; ranking, powing, scaling, indexing 均是用于计算种群适应度的函数; migrate 是种群迁移函数; selecting、 recombin、 mutate 分别是高级的选择、重组和变异函数,对应下方的都是低级的选择、重组和变异函数; reins 是重插入操作函数; *plot 是以 plot 名字结尾的用于可视化输出函数。 *stat 是以 stat 名字结尾的统计函数, *NDSet 是与多目标优化帕累托最优解集的处理有关的函数。
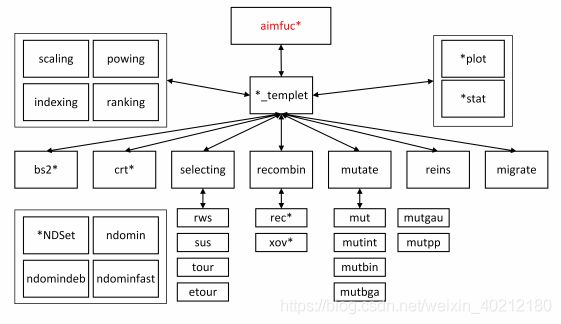
如下为Geatpy的内核函数简要说明,详细的使用方法见说明文档。
- 与初始化种群相关的函数
crtfld(生成区域描述器)
crtbp(创建简单离散种群、二进制编码种群)
crtip(创建整数型种群)
crtpp(创建排列编码种群)
crtrp(创建实数型种群)
meshrng(网格化变量范围)
2.进化迭代
当完成了种群的初始化后,就可以进行遗传进化迭代了。这部分是在进化算法模板里编写的。迭代过程中包括:
调用 ranking 或 scaling 等计算种群适应度。
调用 selecting 进行选择操作 (也可以直接调用低级选择函数)。
调用 recombin 进行重组操作 (也可以直接调用低级重组函数)。
调用 mutate 进行重组操作 (也可以直接调用低级变异函数)。
调用 reins 进行重插入生成新一代种群。
调用 migrate 进行种群迁移 (可以增加种群的多样性)
3.适应度计算
ranking(基于等级划分的适应度分配计算)
scaling(线性尺度变换适应度计算)
indexing(指数尺度变换适应度计算)
powing(幂尺度变换适应度计算)
4.选择
selecting 是高级选择函数,它调用下面的低级选择函数:
sus(随机抽样选择)
rws(轮盘赌选择)
tour(锦标赛选择)
etour(精英锦标赛选择)
5.重组
重组包括了交叉。 recombin 是高级的重组函数,它调用下面的低级重组函数:
recdis(离散重组)
recint(中间重组)
reclin(线性重组)
xovdp(两点交叉)
xovdprs(减少代理的两点交叉)
xovmp(多点交叉)
xovpm(部分匹配交叉)
xovsh(洗牌交叉)
xovshrs(减少代理的洗牌交叉)
xovsp(单点交叉)
xovsprs(减少代理的单点交叉)
- 突变
mutate 是高级的突变函数,它调用下面的低级突变函数:
mut(简单离散变异算子)
mutbga(实数值变异算子)
mutbin(二进制变异算子)
mutgau(高斯突变算子)
mutint(整数值变异算子)
mutpp(排列编码变异算子)
- 重插入
reins 是重插入函数,它将育种个体重插入到父代种群中,生成新一代种群。
- 种群迁移
当使用多种群设计时,可用 migrate 函数实现种群中的个体迁移。
- 染色体解码
对于二进制/格雷编码的种群,我们要对其进行解码才能得到其表现型。
bs2int(二进制/格雷码转整数)
bs2rv(二进制/格雷码转实数)
- 可视化
frontplot(多目标优化帕累托前沿绘图函数)
sgaplot(单目标进化动态绘图函数)
trcplot(单目标进化跟踪器绘图)
- 多目标相关
ndomin(简单非支配排序)
ndomindeb(Deb 非支配排序)
ndominfast(快速非支配排序)
redisNDSet(基于聚集距离的帕累托最优子集筛选)
upNDSet(更新帕累托最优集)
三、使用方法
- 主函数
import numpy as np
import geatpy as ga
import matplotlib.pyplot as plt
from moea_nsga2_templet import moea_nsga2_templet # 导入自定义的进化算法模板
# 数据
seller=np.array([
[1,2120,310,5000,0,1257160,452.7,0.4527],
[2,1320,307,8000,0,736700,426.1,0.4261],
[3,1320,291,8000,0,678810,411.7,0.4117],
[4,1220,285,3000,0,558530,396.4,0.3964],
[5,1220,280,2000,0,606630,365.5,0.3655]
])
buyer=np.array([
[1,132.6,270,7000,0,11547,0,0],
[2,90,286,7000,0,12847,0,0],
[3,99.5,271,9000,0,11912,320.1,0.3201],
[4,102,260,6000,0,13154,325.1,0.3251]
])
Pbi=buyer[:,[2]]*-1
Psj=seller[:,[2]]
P=np.vstack([Pbi,Psj])
n=np.size(P)
vlb=np.zeros(n)
vub=np.hstack([seller[:,3],buyer[:,3]])
ranges=np.vstack([[vlb],[vub]])
b=np.ones(n)
b=np.vstack([[b],[b]])
precisions=(np.ones(n)*3).tolist()
# 获取目标函数地址
AIM_M = __import__('aimfuc')
PUN_M = __import__('punishing')
"""========================遗传算法参数设置========================="""
FieldDR=ga.crtfld(ranges,b,precisions) # 种群区域描述器
problem='R' # 表明是整数问题还是实数问题,'I'表示是整数问题,'R'表示是实数问题
maxormin=-1 # 最小最大化标记
MAXGEN=100 # 最大遗传代数
MAXSIZE=200 # 帕累托最优集最大规模
NIND=100 # 种群规模
SUBPOP=2 # 子种群数量
GGAP=3 # 代沟:子代与父代的重复率为(1-GGAP)
selectStyle='sus' # 遗传算法的选择方式设为"rws"——轮盘赌选择
recombinStyle = 'xovdprs' # 遗传算法的重组方式,设为两点交叉
recopt=1 # 交叉概率
pm = 1 # 变异概率
distribute=True #是否增强帕累托前沿的分布性
drawing=0 # 0表示不绘图,1表示绘制最终结果图,2表示绘制进化过程的动画
#[ObjV, NDSet, NDSetObjV, times] = moea_nsga2_templet(AIM_M, 'aimfuc', None, None, FieldDR, problem, maxormin, MAXGEN, MAXSIZE, NIND, SUBPOP, GGAP, selectStyle, recombinStyle, recopt, pm, distribute, drawing)
#[ObjV, NDSet, NDSetObjV, times]= ga.moea_rwGA_templet(AIM_M, 'aimfuc', None, None, FieldDR, problem, maxormin, MAXGEN, MAXSIZE, NIND, SUBPOP, GGAP, selectStyle, recombinStyle, recopt, pm, distribute, drawing = 0)
#[ObjV, NDSet, NDSetObjV, times]=ga.moea_q_sorted_new_templet(AIM_M, 'aimfuc', None, None, FieldDR, problem, maxormin, MAXGEN, MAXSIZE, NIND, SUBPOP, GGAP, selectStyle, recombinStyle, recopt, pm, distribute, drawing)
[ObjV, NDSet, NDSetObjV, times]=ga.moea_q_sorted_templet(AIM_M, 'aimfuc', None, None, FieldDR, problem, maxormin, MAXGEN, MAXSIZE, NIND, SUBPOP, GGAP, selectStyle, recombinStyle, recopt, pm, distribute, drawing)
#[ObjV, NDSet, NDSetObjV, times]=moea_awGA_templet(AIM_M, 'aimfuc', None, None, FieldDR, problem, maxormin, MAXGEN, MAXSIZE, NIND, SUBPOP, GGAP, selectStyle, recombinStyle, recopt, pm, distribute, drawing)
- 目标函数
import numpy as np
# 定义目标函数
def aimfuc(variables, LegV):
# 数据
seller = np.array([
[1, 2120, 310, 5000, 0, 1257160, 452.7, 0.4527],
[2, 1320, 307, 8000, 0, 736700, 426.1, 0.4261],
[3, 1320, 291, 8000, 0, 678810, 411.7, 0.4117],
[4, 1220, 285, 3000, 0, 558530, 396.4, 0.3964],
[5, 1220, 280, 2000, 0, 606630, 365.5, 0.3655]
])
buyer = np.array([
[1, 132.6, 270, 7000, 0, 11547, 0, 0],
[2, 90, 286, 7000, 0, 12847, 0, 0],
[3, 99.5, 271, 9000, 0, 11912, 320.1, 0.3201],
[4, 102, 260, 6000, 0, 13154, 325.1, 0.3251]
])
Pbi = buyer[:, [2]] * -1
Psj = seller[:, [2]]
P = np.vstack([Psj, Pbi])
kbi = buyer[:, [7]] * -1
ksj = seller[:, [7]]
k = np.vstack([ksj, kbi])
Q = variables[:, :]
#Q=np.transpose(Q)
f1=np.matmul(Q,P)
f2=np.matmul(Q,k)
s=np.size(kbi,None)
t=np.size(ksj,None)
A=np.eye(s+t)#得到对角矩阵
Qxj = seller[:, [5]]
Qki = buyer[:, [4]]
Qli = buyer[:, [5]]
b = np.vstack([Qxj, Qli - Qki])
b = np.transpose(b)
A = np.transpose(A)
c=np.zeros(100)
c=np.vstack(c)
Eb=np.ones(s)*-1
Es=np.ones(t)
E = np.hstack((Es, Eb))
E=np.transpose([E])
#idx1= np.where(np.matmul(Q,A)- 罚函数
import numpy as np
def punishing(LegV, FitnV):
FitnV[np.where(LegV == 0)[0]] = np.min(FitnV) * 0.1 # 对非可行解严厉惩罚
return FitnV
- 基于快速非支配排序法求解多目标优化问题的进化算法
# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ga # 导入geatpy库
import time
def moea_q_sorted_templet(AIM_M, AIM_F, PUN_M, PUN_F, FieldDR, problem, maxormin, MAXGEN, MAXSIZE, NIND, SUBPOP, GGAP, selectStyle, recombinStyle, recopt, pm, distribute, drawing = 1):
"""
moea_q_sorted_templet.py - 基于快速非支配排序法求解多目标优化问题的进化算法模板
语法:
该函数除参数drawing外,不设置可缺省参数。当某个参数需要缺省时,在调用函数时传入None即可。
比如当没有罚函数时,则在调用编程模板时将第3、4个参数设置为None即可,如:
moea_q_sorted_templet(AIM_M, 'aimfuc', None, None, ..., maxormin,...)
输入参数:
AIM_M - 目标函数的地址,由AIM_M = __import__('目标函数所在文件名')语句得到
目标函数规范定义:[f,LegV] = aimfuc(Phen,LegV)
其中Phen是种群的表现型矩阵, LegV为种群的可行性列向量,f为种群的目标函数值矩阵
AIM_F : str - 目标函数名
PUN_M - 罚函数的地址,由PUN_M = __import__('罚函数所在文件名')语句得到
罚函数规范定义: newFitnV = punishing(LegV, FitnV)
其中LegV为种群的可行性列向量, FitnV为种群个体适应度列向量
一般在罚函数中对LegV为0的个体进行适应度惩罚,返回修改后的适应度列向量newFitnV
PUN_F : str - 罚函数名
FieldDR : array - 实际值种群区域描述器
[lb; (float) 指明每个变量使用的下界
ub] (float) 指明每个变量使用的上界
注:不需要考虑是否包含变量的边界值。在crtfld中已经将是否包含边界值进行了处理
本函数生成的矩阵的元素值在FieldDR的[下界, 上界)之间
problem : str - 表明是整数问题还是实数问题,'I'表示是整数问题,'R'表示是实数问题
maxormin int - 最小最大化标记,1表示目标函数最小化;-1表示目标函数最大化
MAXGEN : int - 最大遗传代数
MAXSIZE : int - 帕累托最优集最大规模,当设为np.inf(无穷)时,模板不对帕累托最优解集规模作限制
NIND : int - 种群规模,即种群中包含多少个个体
SUBPOP : int - 子种群数量,即对一个种群划分多少个子种群
GGAP : float - 代沟,表示子代与父代染色体及性状不相同的概率
selectStyle : str - 指代所采用的低级选择算子的名称,如'rws'(轮盘赌选择算子)
recombinStyle: str - 指代所采用的低级重组算子的名称,如'xovsp'(单点交叉)
recopt : float - 交叉概率
pm : float - 重组概率
distribute : bool - 是否增强帕累托前沿的分布性(可能会造成收敛慢或帕累托前沿数目减少)
drawing : int - (可选参数),0表示不绘图,1表示绘制最终结果图,2表示绘制进化过程的动画。
默认drawing为1
算法描述:
本模板维护一个全局帕累托最优集来实现帕累托前沿的搜索
利用快速非支配排序寻找每一代种群的非支配个体,并用它来不断更新全局帕累托最优集,
故并不需要保证种群所有个体都是非支配的
模板使用注意:
1.本模板调用的目标函数形如:[ObjV,LegV] = aimfuc(Phen,LegV),
其中Phen表示种群的表现型矩阵, LegV为种群的可行性列向量(详见Geatpy数据结构)
2.本模板调用的罚函数形如: newFitnV = punishing(LegV, FitnV),
其中FitnV为用其他算法求得的适应度
若不符合上述规范,则请修改算法模板或自定义新算法模板
3.关于'maxormin': geatpy的内核函数全是遵循“最小化目标”的约定的,即目标函数值越小越好。
当需要优化最大化的目标时,需要设置'maxormin'为-1。
本算法模板是正确使用'maxormin'的典型范例,其具体用法如下:
当调用的函数传入参数包含与“目标函数值矩阵”有关的参数(如ObjV,ObjVSel,NDSetObjV等)时,
查看该函数的参考资料(可用'help'命令查看,也可到官网上查看相应的教程),
里面若要求传入前对参数乘上'maxormin',则需要乘上。
里面若要求对返回参数乘上'maxormin'进行还原,
则调用函数返回得到的相应参数需要乘上'maxormin'进行还原,否则其正负号就会被改变。
"""
#==========================初始化配置===========================
# 获取目标函数和罚函数
aimfuc = getattr(AIM_M, AIM_F) # 获得目标函数
if PUN_F is not None:
punishing = getattr(PUN_M, PUN_F) # 获得罚函数
#=========================开始遗传算法进化=======================
if problem == 'R':
Chrom = ga.crtrp(NIND, FieldDR) # 生成实数值种群
elif problem == 'I':
Chrom = ga.crtip(NIND, FieldDR) # 生成整数值种群
LegV = np.ones((NIND, 1)) # 初始化种群的可行性列向量
[ObjV, LegV] = aimfuc(Chrom, LegV) # 计算种群目标函数值
NDSet = np.zeros((0, Chrom.shape[1])) # 定义帕累托最优解记录器
NDSetObjV = np.zeros((0, ObjV.shape[1])) # 定义帕累托最优解的目标函数值记录器
ax = None # 存储上一帧动画
start_time = time.time() # 开始计时
# 开始进化!!
for gen in range(MAXGEN):
# 求种群的非支配个体以及基于被支配数的适应度
[FitnV, frontIdx] = ga.ndominfast(maxormin * ObjV, LegV)
if PUN_F is not None:
FitnV = punishing(LegV, FitnV) # 调用罚函数作进一步的惩罚
# 更新帕累托最优集以及种群非支配个体的适应度
[FitnV, NDSet, NDSetObjV, repnum] = ga.upNDSet(Chrom, maxormin * ObjV, FitnV, NDSet, maxormin * NDSetObjV, frontIdx, LegV)
NDSetObjV *= maxormin # 还原在传入upNDSet函数前被最小化处理过的NDSetObjV
[NDSet, NDSetObjV] = ga.redisNDSet(NDSet, NDSetObjV, NDSetObjV.shape[1] * MAXSIZE) # 利用拥挤距离选择帕累托前沿的子集,在进化过程中最好比上限多筛选出几倍的点集
if distribute == True: # 若要增强种群的分布性(可能会导致帕累托前沿搜索效率降低)
# 计算每个目标下相邻个体的距离(不需要严格计算欧氏距离)
for i in range(ObjV.shape[1]):
idx = np.argsort(ObjV[:, i], 0)
dis = np.diff(ObjV[idx, i]) / (np.max(ObjV[idx, i]) - np.min(ObjV[idx, i]) + 1) # 差分计算距离的偏移量占比,即偏移量除以目标函数的极差。加1是为了避免极差为0
dis = np.hstack([dis, dis[-1]])
FitnV[idx, 0] *= np.exp(dis) # 根据相邻距离修改适应度,突出相邻距离大的个体,以增加种群的多样性
# 进行遗传操作!!
SelCh=ga.selecting(selectStyle, Chrom, FitnV, GGAP, SUBPOP) # 选择
SelCh=ga.recombin(recombinStyle, SelCh, recopt, SUBPOP) #交叉
if problem == 'R':
SelCh=ga.mutbga(SelCh,FieldDR, pm) # 变异
if repnum > Chrom.shape[0] * 0.01: # 当最优个体重复率高达1%时,进行一次高斯变异
SelCh=ga.mutgau(SelCh, FieldDR, pm) # 高斯变异
elif problem == 'I':
SelCh=ga.mutint(SelCh, FieldDR, pm)
LegVSel = np.ones((SelCh.shape[0], 1)) # 初始化育种种群的可行性列向量
[ObjVSel, LegVSel] = aimfuc(SelCh, LegVSel) # 求育种个体的目标函数值
# 求种群的非支配个体以及基于被支配数的适应度
[FitnVSel, frontIdx] = ga.ndominfast(maxormin * ObjVSel, LegVSel)
if PUN_F is not None:
FitnVSel = punishing(LegVSel, FitnVSel) # 调用罚函数作进一步的惩罚
[Chrom,ObjV,LegV] = ga.reins(Chrom,SelCh,SUBPOP,1,0.9,FitnV,FitnVSel,ObjV,ObjVSel,LegV,LegVSel) #重插入
[ObjV, LegV] = aimfuc(Chrom, LegV) # 计算种群目标函数值
if drawing == 2:
ax = ga.frontplot(NDSetObjV, False, ax, gen + 1) # 绘制动态图
end_time = time.time() # 结束计时
[NDSet, NDSetObjV] = ga.redisNDSet(NDSet, NDSetObjV, MAXSIZE) # 最后根据拥挤距离选择均匀分布的点
#=========================绘图及输出结果=========================
if drawing != 0:
ga.frontplot(NDSetObjV,True)
times = end_time - start_time
print('用时:%s 秒'%(times))
print('帕累托前沿点个数:%s 个'%(NDSet.shape[0]))
print('单位时间找到帕累托前沿点个数:%s 个'%(int(NDSet.shape[0] // times)))
# 返回帕累托最优集以及执行时间
return [ObjV, NDSet, NDSetObjV, end_time - start_time]
Geatpy给出的官方文档、demo都很详细,附下载链接