吴恩达机器学习作业Python版作业一.线性回归
吴恩达机器学习作业Python版作业一.线性回归
本练习代码非原创,仅为个人练习记录
参考代码地址 https://blog.csdn.net/Cowry5/article/details/80174130
0. 小练习
利用numpy返回一个5x5单位矩阵
import numpy as np
def warmupExercise():
E5 = np.eye(5) # eye(5)代表5阶单位矩阵
print('这是一个五阶单位矩阵:\n')
print(E5)
1. 单变量线性回归
1.1 题目要求
文件EX1DATA1.TXT包含了我们的线性回归问题的数据集。
第一列是城市的人口,第二列是那个城市的食品卡车的利润。
利用线性回归拟合数据
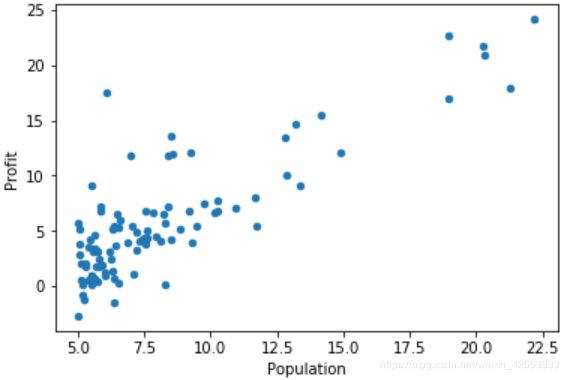
1.2 读取数据,绘制散点图
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
data1 = pd.read_csv('ex1/ex1data1.txt',names=['Population','Profit'])
data1.describe()
data1.plot(x='Population',y='Profit',kind='scatter')
plot.show()
1.3 代价函数
实现并计算代价函数 J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)= \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
其中假设函数 h θ ( x ) = θ T X h_\theta(x)=\theta^TX hθ(x)=θTX
#代价函数 J(θ)
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
# * 在matrix类型中是矩阵的叉乘,multiply是对应元素相乘
# * 在ndarray类型中,dot或 @ 是叉乘,* 是对应元素相乘
增加 x 0 x_0 x0
data1.insert(0, 'Ones', 1)
给X, y, theta赋值
cols = data1.shape[1] # 列数
X = data1.iloc[:,0:cols-1] # 取前几列
y = data1.iloc[:,[cols-1]] # 取最后一列,即目标向量
转化为np.matrix
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix([0,0])
查看X.shape, theta.shape, y.shape
X.shape, theta.shape, y.shape
#((97, 2), (1, 2), (97, 1))
计算代价函数
computeCost(X, y, theta)
#32.072733877455676
1.4 重点 — 批量梯度下降
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta) θj:=θj−α∂θj∂J(θ)
θ j : = θ j − α 1 m J ( θ ) ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\alpha\frac{1}{m}J(\theta)\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−αm1J(θ)i=1∑m(hθ(x(i))−y(i))xj(i)
以下代码建议用纸笔简单代入一遍方便理解
#通过梯度下降法来求使代价函数最小的参数theta
def gradientDescent(X, y, theta, alpha, epoch):
temp = np.matrix(np.zeros(theta.shape)) # 初始化一个θ临时矩阵
parameters = int(theta.ravel().shape[1]) # 参数θ的数量
cost = np.zeros(epoch) # 初始化一个ndarray,包含每次epoch的cost
m = X.shape[0] # 样本的数量
for i in range(epoch):
# 利用向量化一步求解
temp = theta - (alpha / m) * (X * theta.T - y).T * X
theta = temp
cost[i] = computeCost(X, y, theta)
# 以下是不用向量化求解梯度下降
# error = (X * theta.T) - y # (97, 1)
# for j in range(parameters):
# term = np.multiply(error, X[:,j]) # (97, 1)
# temp[0,j] = theta[0,j] - ((alpha / m) * np.sum(term)) # (1,1)
return theta, cost
开始求解,代入参数并计算
alpha = 0.01
epoch = 1000
final_theta, cost = gradientDescent(X, y, theta, alpha, epoch)
print(final_theta)
print(computeCost(X, y, final_theta))
print(cost.min())
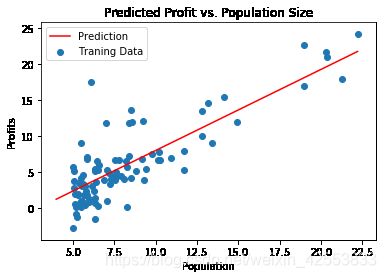
1.5 绘制拟合曲线及数据
x = np.linspace(4, data1.iloc[:,[1]].max(), 100)
f = final_theta[0, 0] + (final_theta[0, 1] * x)
fig, ax = plt.subplots(figsize=(6,4))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data1['Population'],data1['Profit'], label='Traning Data')
ax.legend(loc=2) # 2表示在左上角
ax.set_xlabel('Population')
ax.set_ylabel('Profits')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
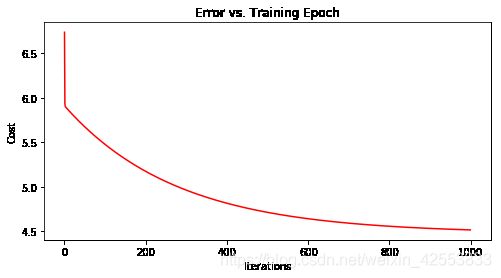
1.5 绘制迭代次数与代价的关系曲线
fig,ax = plt.subplots(figsize=(8,4))
ax.plot(np.arange(epoch), cost, 'r') # np.arange()返回等差数组
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
2 多变量线性回归
2.1 题目要求
文件EX1DATA2.TXT包含了我们的线性回归问题的数据集。
利用线性回归拟合数据,其中有2个变量(房子大小,卧室数量)和目标(房子价格)。
2.2 读取数据
data = pd.read_csv('ex1/ex1data2.txt',names=['size','bedrooms','price'])
data.head()
2.3 特征归一化
data = (data - data.mean()) / data.std()
data.head()
2.4 添加 x 0 x_0 x0,赋值
data.insert(0,'one',1)
data.head()
X2 = data.iloc[:,0:3]
y2 = data.iloc[:,[3]]
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix([0,0,0])
查看数据形状
X2.shape, theta2.shape, y2.shape
#((47, 3), (1, 3), (47, 1))
2.5 初始代价
computeCost(X2,y2,theta2)
#0.48936170212765967
2.6 批量梯度下降
final_theta2, cost2 = gradientDescent(X2, y2, theta2, alpha, epoch)
computeCost(X2, y2, final_theta2)
#0.13070336960771892
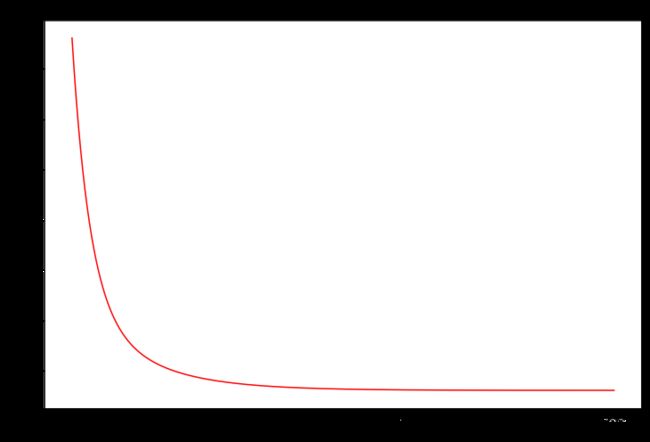
2.7 绘制迭代次数与代价的关系曲线
fig2, ax2 = plt.subplots(figsize=(12,8))
ax2.plot(np.arange(epoch), cost2, 'r')
ax2.set_xlabel('Iterations')
ax2.set_ylabel('Cost')
ax2.set_title('Error vs. Training Epoch')
plt.show()
3 正规方程求解数据1,2
正规方程
def normalEqn(X,y):
theta = np.linalg.inv(X.T@X)@X.T@y
return theta
求解数据1
thetazz = normalEqn(X,y)
computeCost(X,y,thetazz.T)
#4.476971375975179
求解数据2
thetass = normalEqn(X2,y2)
computeCost(X2,y2,thetass.T)
#0.130686480539042