力扣高频|算法面试题汇总(四):堆、栈与队列
力扣高频|算法面试题汇总(一):开始之前
力扣高频|算法面试题汇总(二):字符串
力扣高频|算法面试题汇总(三):数组
力扣高频|算法面试题汇总(四):堆、栈与队列
力扣高频|算法面试题汇总(五):链表
力扣高频|算法面试题汇总(六):哈希与映射
力扣高频|算法面试题汇总(七):树
力扣高频|算法面试题汇总(八):排序与检索
力扣高频|算法面试题汇总(九):动态规划
力扣高频|算法面试题汇总(十):图论
力扣高频|算法面试题汇总(十一):数学&位运算
力扣高频|算法面试题汇总(四):堆、栈与队列
力扣链接
目录:
- 1.最小栈
- 2.数组中的第K个最大元素
- 3.数据流的中位数
- 4.有序矩阵中第K小的元素
- 5.前 K 个高频元素
- 6.滑动窗口最大值
- 7.基本计算器 II
- 8.扁平化嵌套列表迭代器
- 9.逆波兰表达式求值
1.最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
示例:
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示:
pop、top 和 getMin 操作总是在 非空栈 上调用。
C++
class MinStack {
private:
vector<int> nums;
public:
/** initialize your data structure here. */
MinStack() {
}
void push(int x) {
nums.push_back(x);
}
void pop() {
nums.pop_back();
}
int top() {
return nums[nums.size() - 1];
}
int getMin() {
int min = nums[0];
for(auto num : nums){
if(num < min)
min = num;
}
return min;
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(x);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/
Python
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.nums = []
def push(self, x: int) -> None:
self.nums.append(x)
def pop(self) -> None:
self.nums.pop()
def top(self) -> int:
return self.nums[len(self.nums) - 1]
def getMin(self) -> int:
min = self.nums[0]
for num in self.nums:
if num < min:
min = num
return min
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()
2.数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
思路1:
排序后查找。
使用默认排序算法的复杂度:算法的时间复杂度为 O ( N l o g N ) O(Nlog N) O(NlogN),空间复杂度为 O ( 1 ) O(1) O(1)。
C++
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
sort(nums.begin(), nums.end());
return nums[nums.size() - k];
}
};
Python
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
nums = sorted(nums)
return nums[len(nums) - k]
思路2:
参考官方思路,使用大顶堆,保留k个最大的数。
向大小为 k 的堆中添加元素的时间复杂度为 O ( l o g k ) O(logk) O(logk),我们将重复该操作 N 次,故总时间复杂度为 {O}(N \log k)O(Nlogk)。
在 Python 的 heapq 库中有一个 nlargest 方法,具有同样的时间复杂度,能将代码简化到只有一行。
C++
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int,vector<int>,greater<int>> q;
for(auto it:nums){
q.push(it);
if(q.size()>k) q.pop();
}
return q.top();
}
};
Python
class Solution:
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
return heapq.nlargest(k, nums)[-1]
3.数据流的中位数
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例:
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
进阶:
如果数据流中所有整数都在 0 到 100 范围内,你将如何优化你的算法?
如果数据流中 99% 的整数都在 0 到 100 范围内,你将如何优化你的算法?
思路1:
暴力法,每次获取中位数时就进行排序获取,超时。
思路2:
使用最大堆和最小堆,参考剑指offer:数据流中的中位数
C++
class MedianFinder {
private:
// 最大堆
vector<int> maxheap;
// 最小堆
vector<int> minheap;
public:
/** initialize your data structure here. */
MedianFinder() {
}
void addNum(int num) {
int size = maxheap.size() + minheap.size();
// 如果当前数目是偶数个,默认把num放进最小堆
if((size & 1) == 0){
int temp = num;
//如果最大堆不为空,且输入的数字小于最大堆的最大值
if(!maxheap.empty() && num < maxheap[0]){
// 把最大的数字拿出来
temp = maxheap[0];
// 再把数字放进最大堆
maxheap[0] = num;
// 重新生成最大堆
make_heap(maxheap.begin(), maxheap.end());
}
// 把元素放进最小堆
minheap.push_back(temp);
// 重新生成最小堆
push_heap(minheap.begin(), minheap.end(), greater<int>());
}else{
// 如果当前数目是奇数个,默认把num放进最大堆
int temp = num;
// 如果最小堆不为空,且输入的数字大于最小堆的最小值
if(!minheap.empty() && num > minheap[0]){
temp = minheap[0]; // 把最小的数字拿出来
minheap[0] = num; // 把输入的数字放进最小堆
make_heap(minheap.begin(), minheap.end(), greater<int>());
}
// 把元素放进最大堆
maxheap.push_back(temp);
// 重新生成最大堆
push_heap(maxheap.begin(), maxheap.end());
}
}
double findMedian() {
int size = maxheap.size() + minheap.size();
double res;
if(size & 1){
res = minheap[0];
}else{
res = (maxheap[0] + minheap[0])*0.5;
}
return res;
}
};
很迷,在最后一个测试用例超时了,所以参考官方实现。
class MedianFinder {
priority_queue<int> maxheap; // 最大堆 降序
priority_queue<int, vector<int>, greater<int>> minheap; // 最小堆 升序
public:
// Adds a number into the data structure.
void addNum(int num)
{
maxheap.push(num); // 把数字添加到最大堆中
minheap.push(maxheap.top()); // 把最大堆的最大值放进最小堆中
maxheap.pop(); // 弹出最大堆最大值
// 如果最大堆的元素个数小于最小堆的个数
if (maxheap.size() < minheap.size()) {
// maintain size property
maxheap.push(minheap.top()); // 把最小堆的最小值放进最大堆
minheap.pop(); // 弹出最小堆最小值
}
}
// Returns the median of current data stream
double findMedian()
{
// 默认最大堆的元素个数大于最小堆元素个数
return maxheap.size() > minheap.size() ? (double) maxheap.top() : (maxheap.top() + minheap.top()) * 0.5;
}
};
Python
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
self.minheap = [] # 最小堆
self.maxheap = [] # 最大堆
def addNum(self, num: int) -> None:
# 默认把元素添加到最大堆
heapq.heappush(self.maxheap, (-num, num)) # python默认最小堆,模拟最大堆
# 把最大堆最大值元素给最小堆
heapq.heappush(self.minheap, self.maxheap[0][1])
# 弹出最大堆的最大值
heapq.heappop(self.maxheap)
# 如果最大堆的元素个数少于最小堆数量,把最小堆的最小值给最大堆
if len(self.maxheap) < len(self.minheap):
heapq.heappush(self.maxheap, (-self.minheap[0], self.minheap[0]))
heapq.heappop(self.minheap)
def findMedian(self) -> float:
size = len(self.minheap) + len(self.maxheap)
# 如果是奇数
if size & 1:
return self.maxheap[0][1]
else:
return (self.maxheap[0][1] + self.minheap[0])*0.5
4.有序矩阵中第K小的元素
给定一个 n x n 矩阵,其中每行和每列元素均按升序排序,找到矩阵中第k小的元素。
请注意,它是排序后的第 k 小元素,而不是第 k 个不同的元素。
示例:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
返回 13。
提示:
你可以假设 k 的值永远是有效的, 1 ≤ k ≤ n2 。
思路1:
使用堆排序,时间复杂度为 O ( n 2 l o g ( k ) ) O(n^2log(k)) O(n2log(k)),空间复杂度为 O ( k ) O(k) O(k)。用最大堆保存最小的k个数,堆顶就是第k小的数。由于矩阵大小是有顺序的,还可以有优化空间:如果该行元素大于堆顶,则可以直接中断该循环,因为不可能还存在比堆顶还小的元素,进入下一个循环。
C++
class Solution {
public:
int kthSmallest(vector<vector<int>>& matrix, int k) {
// 创建大顶堆,保存最小的k个元素
priority_queue<int> maxheap;
for(int col = 0; col < matrix[0].size(); ++col)
for(int row = 0; row < matrix.size(); ++row){
if(maxheap.size() < k ){
// 放进元素
maxheap.push(matrix[row][col]);
}else if(maxheap.top() > matrix[row][col]){
// 如果矩阵元素小于最大堆的最大值
// 弹出最大值
maxheap.pop();
maxheap.push(matrix[row][col]);
}else{
// 矩阵每行是从小到大,则右边的元素不可能还小于最大堆最大值
break;
}
}
return maxheap.top();
}
};
Python
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
# 最大堆
maxheap = [] # 最大堆
for row in range(len(matrix)):
for col in range(len(matrix[0])):
if len(maxheap) < k:
heapq.heappush(maxheap, (-matrix[row][col], matrix[row][col])) # python默认最小堆,模拟最大堆
elif maxheap[0][1] > matrix[row][col]:
# 弹出最大堆的最大值
heapq.heappop(maxheap)
# 添加元素
heapq.heappush(maxheap, (-matrix[row][col], matrix[row][col]))
else:
break
return maxheap[0][1]
思路2:
二分法。参考思路如下:
首先第k大数一定落在[l, r]中,其中l = matrix[0][0], r = matrix[row - 1][col - 1].
我们二分值域[l, r]区间,mid = (l + r) >> 1, 对于mid,检查矩阵中有多少元素小于等于mid,记个数为cnt,那么有:
- 1、如果
cnt < k, 那么[l, mid]中包含矩阵元素个数一定小于k,那么第k小元素一定不在[l, mid]中,必定在[mid +1, r]中,所以更新l = mid + 1. - 2、否则
cnt >= k,那么[l, mid]中包含矩阵元素个数就大于等于k,即第k小元素一定在[l,mid]区间中,更新r = mid;
算法时间复杂度为 O ( n ∗ l o g ( m ) ) O(n * log(m)) O(n∗log(m)), 其中n = max(row, col),代表矩阵行数和列数的最大值, m代表二分区间的长度,即矩阵最大值和最小值的差。
C++
class Solution {
public:
int kthSmallest(vector<vector<int>>& matrix, int k) {
int rows = matrix.size();
int cols = matrix[0].size();
// 使用二分法
int low = matrix[0][0];
int high = matrix[rows - 1][cols - 1];
while(low < high){
int mid = low + (high - low)/2;
int count = findCount(matrix, mid);
// 如果比mid小的数字小于k, 说明第k小的数字大于当前mid
if(count < k)
low = mid + 1;
else
high = mid;
}
return low;
}
int findCount(vector<vector<int>>& matrix, int mid){
// 利用矩阵特性从左小角开始查找
int count = 0;
int rows = matrix.size();
int cols = matrix[0].size();
int row = rows-1;
int col = 0;
while( row >= 0 && col <= cols - 1){
if(matrix[row][col] > mid){
// 先减行数
--row;
}else{
// 跳过这一列
count += row+1;
// 移动
++col;
}
}
return count;
}
};
Python
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
# 二分法
low = matrix[0][0]
rows = len(matrix)
cols = len(matrix[0])
high = matrix[rows - 1][cols - 1]
while low < high:
mid = low + (high - low)/2
count = self.findCount(matrix , mid)
if count < k:
low = mid + 1
else:
high = mid
return int(low)
def findCount(self, matrix , mid):
rows = len(matrix)
cols = len(matrix[0])
col = 0
row = rows - 1
count = 0
while row >= 0 and col <= cols - 1:
if matrix[row][col] > mid:
row -= 1
else:
count += row + 1
col += 1
return count
5.前 K 个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
你可以按任意顺序返回答案。
思路:
首先使用哈希表记录每个数字出现的频率,解这使用最小堆进行存储数字出现的频率,用来保存前k个高频元素出现的频率。
C++
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
// 用哈希表存储每个id出现的次数
unordered_map<int, int> idCount;
for(auto num : nums){
if(idCount.find(num) == idCount.end())
idCount[num] = 1;
else
++idCount[num];
}
// 使用最小堆来保存出现频率最高的k个元素
vector<int> minheap;
for(auto x : idCount){
minheap.push_back(x.second);
// 当已建堆的容器范围内有新的元素插入末尾后,应当调用push_heap将该元素插入堆中。
push_heap(minheap.begin(), minheap.end(), greater<int>());
if(minheap.size() > k){
// 将堆顶(所给范围的最前面)元素移动到所给范围的最后,并且将新的最小值置于所给范围的最前面
pop_heap(minheap.begin(), minheap.end(), greater<int>());
// 弹出最小堆最小的那个元素
minheap.pop_back();
}
}
vector<int> ans;
for(auto x : idCount){
// 在最小堆中招对应的id,以及保证结果不存在这个数字,以免重复记录
if(find(minheap.begin(), minheap.end(), x.second) != minheap.end() && find(ans.begin(), ans.end(), x.first) == ans.end()){
ans.push_back(x.first);
}
}
return ans;
}
};
Python:
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
idHash = dict()
for num in nums:
if not num in idHash:
idHash[num] = 1
else:
idHash[num] += 1
# 建立最小堆
minheap = []
for key in idHash:
heapq.heappush(minheap, (idHash[key], key))
if len(minheap) > k:
# 弹出
heapq.heappop(minheap)
# 变最小堆
# heapq.heapify(minheap)
ans = []
for value, key in minheap:
ans.append(key)
return ans
6.滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
这题剑指offer做过,具体思路见剑指offer|解析和答案(C++/Python) (五)上:滑动窗口最大值
C++
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> maxvalue;
// 新建队列进行保存最大值的索引
deque<int> index;
for(int i = 0; i < k; ++i){
// 确保索引的值是保留的最大值
while(!index.empty() && nums[i]>= nums[index.back()])
index.pop_back();
// 添加索引
index.push_back(i);
}
for(int i = k; i < nums.size(); ++i){
// 添加最大值
maxvalue.push_back(nums[index.front()]);
// 确保索引的值是保留的最大值
while(!index.empty() && nums[i]>= nums[index.back()])
index.pop_back();
// 如果最大值溢出滑动框
if(!index.empty() && index.front() <= (i - k))
index.pop_front();
index.push_back(i);
}
// 加入最后一个值
maxvalue.push_back(nums[index.front()]);
return maxvalue;
}
};
Python
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
maxValue = list()
if len(nums) > 0 and k > 0:
index = []
for i in range(k):
while len(index) > 0 and nums[i] >= nums[index[-1]]:
index.pop()
index.append(i)
for i in range(k, len(nums)):
maxValue.append(nums[index[0]])
while len(index) > 0 and nums[i] >= nums[index[-1]]:
index.pop()
if len(index) > 0 and index[0] <= (i-k):
index.pop(0)
index.append(i)
maxValue.append(nums[index[0]])
return maxValue
7.基本计算器 II
实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式仅包含非负整数,+, - ,,/ 四种运算符和空格 。 整数除法仅保留整数部分。
示例 1:
输入: "3+22"
输出: 7
示例 2:
输入: " 3/2 "
输出: 1
示例 3:
输入: " 3+5 / 2 "
输出: 5
说明:
你可以假设所给定的表达式都是有效的。
请不要使用内置的库函数 eval。
思路:
参考使用栈的方式来保存计算结果。利用栈的方式解决运算优先级的问题 当为加减时放入栈中 当为乘除时讲栈顶元素与最近获得一个数进行运算,同时把栈顶元素弹出,放进计算之后的元素。最后把栈的所有元素加起来即可。
C++
class Solution {
public:
int calculate(string s) {
long result = 0;
long num = 0;
// 初始上一个运算符为加法 上个数字为0
char op = '+';
char c;
// 用栈来保存结果
vector<int> stack;
for(int i = 0; i < s.length(); ++i){
c = s[i];
if(c >='0'){
// 计算数字
num = num * 10 + c- '0';
}
// 当遇到符号时,或者是到了字符串末尾
if(c < '0' && c != ' '|| i == s.length() -1){
// 此时op是上一次遇到的符号
if(op == '+') stack.push_back(num);
if(op == '-') stack.push_back(-num);
if(op == '*' || op =='/'){
int temp = (op == '*')? stack.back() * num : stack.back()/num;
// 弹出上一个值
stack.pop_back();
// 重新放进计算的结果
stack.push_back(temp);
}
// 获取当前op符号
op = s[i];
num = 0;
}
}
while(!stack.empty()){
result += stack.back();
stack.pop_back();
}
return result;
}
};
Python
class Solution:
def calculate(self, s: str) -> int:
stack = []
num = 0
res = 0
op = '+'
ops = ['+', '-', '*', '/']
for i in range(len(s)):
# s[i] != ' ' 很重要
if not s[i] in ops and s[i] != ' ':
num = num*10 + int(s[i])
if s[i] in ops and s[i] != ' ' or i == len(s) - 1:
if op == '+':
stack.append(num)
if op == '-':
stack.append(-num)
if op == '*' :
temp = stack[-1]*num
stack.pop()
stack.append(int(temp))
if op == '/':
temp = stack[-1]/num
stack.pop()
stack.append(int(temp))
num = 0
op = s[i]
for num in stack:
res += num
return res
8.扁平化嵌套列表迭代器
扁平化嵌套列表迭代器
给你一个嵌套的整型列表。请你设计一个迭代器,使其能够遍历这个整型列表中的所有整数。
列表中的每一项或者为一个整数,或者是另一个列表。其中列表的元素也可能是整数或是其他列表。
示例 1:
输入: [[1,1],2,[1,1]]
输出: [1,1,2,1,1]
解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,1,2,1,1]。
示例 2:
输入: [1,[4,[6]]]
输出: [1,4,6]
解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,4,6]。
这题没怎么看明白,先放一下。
C++
class NestedIterator {
private:
stack<NestedInteger> s;
public:
NestedIterator(vector<NestedInteger> &nestedList) {
// 添加元素
for(int i = nestedList.size() - 1; i >= 0; --i)
s.push(nestedList[i]);
}
int next() {
NestedInteger temp = s.top(); // 获取栈顶元素
s.pop(); // 弹出栈顶
return temp.getInteger();
}
bool hasNext() {
while(!s.empty()){
NestedInteger temp = s.top();
if(temp.isInteger())
return true;
s.pop();
for(int i = temp.getList().size() - 1; i >= 0; --i)
s.push(temp.getList()[i]);
}
return false;
}
};
还有其他思路:C++ 综合各路大佬的答案
Python:
来自:栈+迭代,5行代码简单易理解
class NestedIterator:
def __init__(self, nestedList: [NestedInteger]):
# 对于nestedList中的内容,我们需要从左往右遍历,
# 但堆栈pop是从右端开始,所以我们压栈的时候需要将nestedList反转再压栈
self.stack = nestedList[::-1]
def next(self) -> int:
# hasNext 函数中已经保证栈顶是integer,所以直接返回pop结果
return self.stack.pop(-1).getInteger()
def hasNext(self) -> bool:
# 对栈顶进行‘剥皮’,如果栈顶是List,把List反转再依次压栈,
# 然后再看栈顶,依次循环直到栈顶为Integer。
# 同时可以处理空的List,类似[[[]],[]]这种test case
while len(self.stack) > 0 and self.stack[-1].isInteger() is False:
self.stack += self.stack.pop().getList()[::-1]
return len(self.stack) > 0
9.逆波兰表达式求值
根据逆波兰表示法,求表达式的值。
有效的运算符包括 +, -, , / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入: [“2”, “1”, “+”, “3”, ""]
输出: 9
解释: ((2 + 1) * 3) = 9
示例 2:
输入: [“4”, “13”, “5”, “/”, “+”]
输出: 6
解释: (4 + (13 / 5)) = 6
思路:
这个在《大话数据结构上》看到过。使用栈数据结构。规则:从左到右遍历表达式的每个数字和符号,遇到是数字就进栈,遇到是符号,就将处于栈顶的两个数字弹出,进行运算,运算结果进钱, 直到最终获得结果。
举例后缀表达式:931 - 3*+102 / +,以下图片来自《大话数据结构上》:

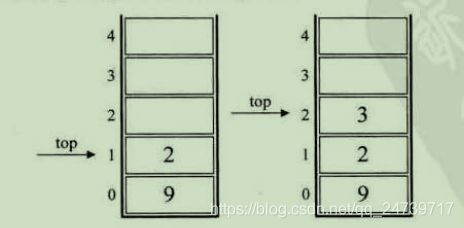
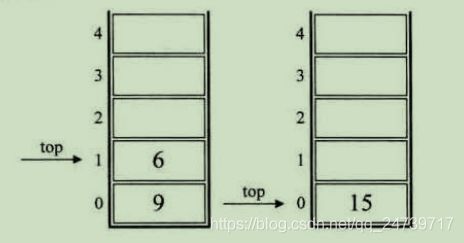
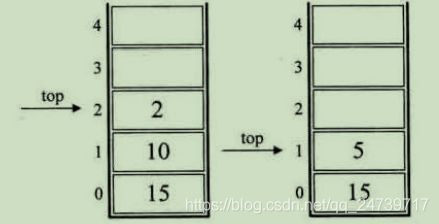

C++
class Solution {
public:
int evalRPN(vector<string>& tokens) {
// 用栈来存储数字
vector<int> nums;
for(int i = 0; i < tokens.size(); ++i){
if(tokens[i] != "+" && tokens[i] != "-" && tokens[i] != "*" && tokens[i] != "/"){
nums.push_back(stoi(tokens[i]));
}else if(tokens[i] == "+"){
int add1 = nums.back();
nums.pop_back();
int add2 = nums.back();
nums.pop_back();
add2 = add2 + add1;
nums.push_back(add2);
}else if(tokens[i] == "-"){
int sub1 = nums.back();
nums.pop_back();
int sub2 = nums.back();
nums.pop_back();
sub2 = sub2 - sub1;
nums.push_back(sub2);
}else if(tokens[i] == "*"){
int mul1 = nums.back();
nums.pop_back();
int mul2 = nums.back();
nums.pop_back();
mul2 = mul2 * mul1;
nums.push_back(mul2);
}else if(tokens[i] == "/"){
int div1 = nums.back();
nums.pop_back();
int div2 = nums.back();
nums.pop_back();
div2 = div2 / div1;
nums.push_back(div2);
}
}
return nums[0];
}
};
还有范例,很优美:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
if(tokens.size()==0) return 0;
stack<int> s;
int temp=0;
for(int i=0;i<tokens.size();i++){
if(tokens[i][0]<='9'&&tokens[i][0]>='0'||(tokens[i].size()>1&&tokens[i][0]=='-')){
s.push(atoi(tokens[i].c_str()));
}else{
int a=s.top();
s.pop();
int b=s.top();
s.pop();
if(tokens[i][0]=='+') temp=a+b;
if(tokens[i][0]=='-') temp=b-a;
if(tokens[i][0]=='*') temp=a*b;
if(tokens[i][0]=='/') temp=b/a;
s.push(temp);
}
}
return s.top();
}
};
Python:
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
nums = []
ops = ["+", "-", "*", "/"]
for i in range(len(tokens)):
if not tokens[i] in ops:
nums.append(int(tokens[i]))
elif tokens[i] == "+":
add1, add2 = nums[-2], nums[-1]
nums.pop()
nums.pop()
add1 = add1 + add2
nums.append(int(add1))
elif tokens[i] == "-":
sub1, sub2 = nums[-2], nums[-1]
nums.pop()
nums.pop()
sub1 = sub1 - sub2
nums.append(int(sub1))
elif tokens[i] == "*":
mul1, mul2 = nums[-2], nums[-1]
nums.pop()
nums.pop()
mul1 = mul1 * mul2
nums.append(int(mul1))
elif tokens[i] == "/":
div1, div2 = nums[-2], nums[-1]
nums.pop()
nums.pop()
div1 = div1 / div2
nums.append(int(div1))
return nums[0]