算法学习之模拟退火算法路径规划(python代码实现)
模拟退火算法路径规划(python代码实现)
- 一、引言
- 二、算法介绍以及伪代码
-
- 1、算法通俗介绍
- 2、路径规划算法伪代码
- 三、算法流程及代码实现
-
- 1、地图创建
- 2、初始化路径
-
- 小结
- 3、计算适应度值
- 4、5、产生新路径并计算适应度值
- 6、判断是否接受新路径
- 7、输出结果
- 四、代码总工程
- 五、结束语
一、引言
机器人控制过程中,路径规划是其中重要的一环。因此本文采用模拟退火算法对机器人移动时的路径进行优化,最终选取出一条最优路径。采用栅格图法为机器人移动的地图进行建模,并根据模拟退火算法机理,在python上仿真实现了最优路径的选取。
本方法与遗传算法有类似之处,对比上一篇博客可以加深理解:算法学习之遗传算法路径规划(python代码实现)
二、算法介绍以及伪代码
1、算法通俗介绍
在说模拟退火算法之前,要先引入穷举法、蒙特卡洛法、爬山法,下面开始一个一个介绍。
首先给定一个函数,要求求出函数在定义域中的最大值。 f ( x ) = 11 ∗ s i n ( x ) + 7 ∗ c o s ( 5 ∗ x ) f(x) = 11*sin(x) + 7*cos(5*x) f(x)=11∗sin(x)+7∗cos(5∗x) x = [ − 3 , 3 ] x=[-3,3] x=[−3,3]
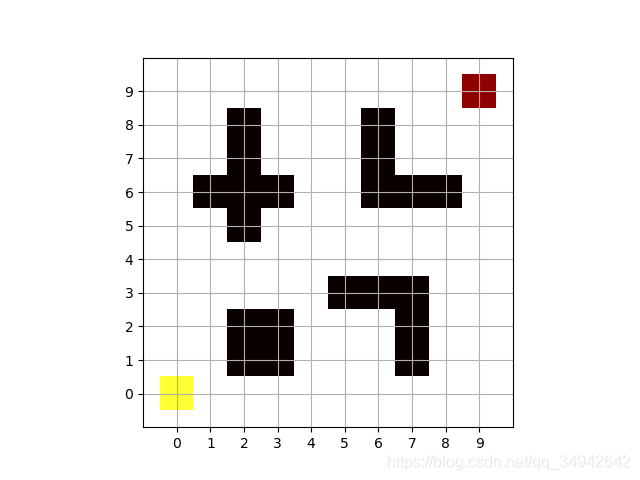
这是一个一元函数,公式求解的话也很简单。那么现在用以上列出的算法来求解 算法伪代码如下: 采用栅格图法构建地图。首先用列表创建一个10*10的矩阵,矩阵元素中值分别表示不同的涵义,数值不同含义不同,具体解释在下面代码中有注释。然后利用matplotlib包中的pylab库,把矩阵用热力图的形式画出来。具体操作如下代码所示: 上示代码运行后为原始地图,左下角黄色为起点,右上角为终点,黑色为障碍区域。 模拟退火算法路径规划中初始化一条随机路径,这里的操作与上篇博客中遗传算法初始化种群类似,不过遗传算法初始化的是种群,而模拟退火算法只需要一条路径(就是种群中的个体)就可以。 模拟退火算法初始化路径的方法和遗传算法初始化种群的方法总体思想一致,但一些小的细节做了修改,在遗传算法中初始化路径时,若一条路径连续化不成功就放弃这条路径,因为它有种群的概念,所以无论如何都会有连续化成功的路径。而模拟退火算法初始化的路径只需要一条,若是放弃了连续不成功的路径,那么就没有初始路径了,因此在本文的代码中加入了一个while循环判断,防止初始化路径不成功。 路径规划中适应度函数就是求解路径长度的函数,适应度值就是路径长度。代码中给定相邻的栅格图为1个单位长度,则对角的长度为1.4(根号2)。具体解释参照遗传算法博客,与遗传算法不同的一点是,模拟退火算法计算出来的适应度值就是一个数值,而遗传算法计算出来的是,路径长度数值组成的列表,也就是列表中的每一个元素就是路径长度。 产生的新路径是在前一个路径的信息基础上产生的,因此模拟退火算法也算是启发式搜索算法,新的路径从上一个路径的信息中获得。在本文中,采用的是遗传算法中变异的操作来获得新的路径。 注意两点:这条新路径是在原路径基础上得到的;这条路径的长度和原路径的长度可能相等、可能大于、可能小于。因此新的路径长度要与原路径长度比较,来判断是否接受这条新的路径。 与伪代码中的方法一致:如果新路径的长度小于原路径的长度,则用新路径更新原路径的信息;若新路径的长度大于原路径的长度,则计算接受此条新路径的概率,称为接受概率。在随机产生一个0-1的随机数,若接受概率大于随机数,则用新路径更新原路径的信息,否则放弃新的路径,依旧使用原路径进行搜索。 其中两个for循环,外层循环是温度变化次数,每次迭代会将温度以下降系数步长下降;内层循环是每个温度下迭代的次数。总共迭代次数是两个数值的乘积。 以上主函数运行完毕之后,就会得到模拟退火算法搜索的最优路径。代码运行结果如下: 又到了最终展现代码的时刻,总工程如下: 整体来说,模拟退火算法是比较简单的,因为先了解了遗传算法,在了解这个算法的时候是事半功倍。但是也因为模拟退火算法简单,因此改进的点就少了许多,创新点少,改进算法发论文也会很难。最多的是从接受概率入手创新。
1、穷举法:它的做法是在解空间中,按照一定的规则,枚举出所有的解,然后再一一比对,最终获得最优解。
以本函数为例,比如选定一个初始解为-3,那么按照一定的规则,在这里按照函数的解每次递增0.1的规则,把所有解空间的解枚举出来,列完之后求出每个解的函数值,找出使函数值最大的解,就是这个函数的最优解。这种方法的缺点一目了然,比如每次将解递增3,那么,,,,,没了呀
2、蒙特卡洛法:它的做法是在解空间中,随机选取若干个解,这个若干个,是人为指定的,比如我指定随机生成100个解,然后把这100个解的函数值算出来,找出最大的,也能解决问题。但如果解空间是无边界的,并且函数如果是二元函数呢,,,
也因此出现了盲目搜索和启发式搜索的类别,以上两种方法都是盲目搜索方法,而下面介绍启发式搜索方法。
3、爬山法:爬山法就是一种启发式搜索,因为它每一次产生的新解,都会从前一个解中获取一定的信息,来判断这个新解是否更接近最优解。下面是f(x)在[-3,3]之间的函数图像,可以看到,函数的最大值解大约在1.3附近。而图像中还有一个红色的点,这个是爬山法随机产生的初始解。下面利用爬山法求这个函数的解:
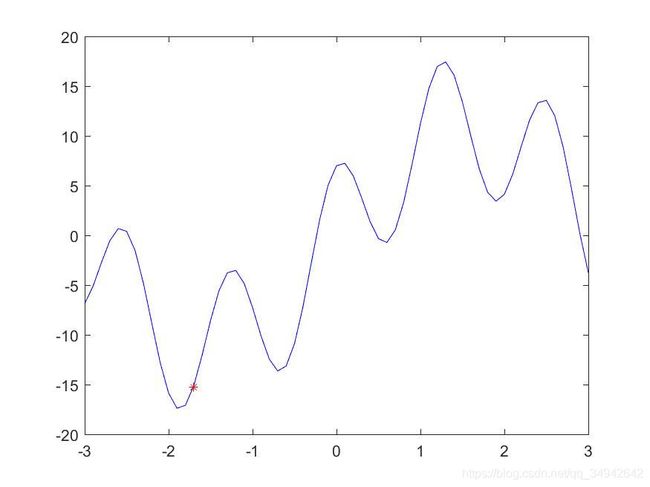
step1:首先随机产生一个初始解,假设是图中红色的点
step2:在初始解的邻域范围内搜索下一个解,这个搜索方向可以向左邻域搜索,也可以向右边搜索。搜索以一定的步长来求下一个解,步长越小,搜索的时间也会越长,但是步长越大,有可能跳过最优解。因此还是取较小一点的步长。
step3:比较向左走和向右走两个方向的函数值,因为要求函数值最大,在图中可以看出,往右走使函数值增大,因此选择向右爬。
step4:不断重复2.3步骤,知道找到一个极大值,或者达到指定的寻找次数,结束搜索
以上步骤请注意在step4中终止条件是找到极大值,而不是最大值,这个是什么原因呢,原因请看下图:
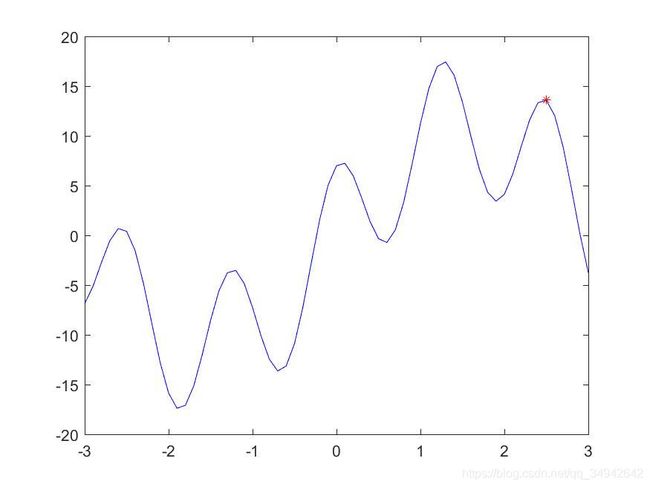
图中可以看到红色的点在一个极大值点处,那么无论往左走还是往右走,都是使函数值下降的方向,因此,爬山法会认为,当前值就是最大值,那么就会结束搜索。再多说一下,爬山算法也属于贪心算法一类的,因为它只能看得到眼前的最优,看不到全局的最优,错把局部当全局,不对局部最优解放手,就造成了得不到全局最优解的结果。
所以,通过分析爬山法,可以看出爬山法极容易找到极值点,而不是最值点,这个与初始解的位置有很大的关系。因此为了改善爬山法的缺陷,就需要采用模拟退火方法。
4、模拟退火算法:
模拟退火算法原理是依据金属物质退火过程和优化问题之间的相似性。物质在加热的时候,粒子间的布朗运动增强,到达一定强度后在进行退火,粒子热运动减弱,并逐渐趋于有序,最后达到稳定。
这段话我的理解是:物体在在加热过程中,粒子之间的运动非常活跃,映射到爬山过程中,就是此时爬山人的能力非常强,能从一个山头跳到另一个山头上,此时可以完美解决爬山算法中陷入局部最优的问题,此时要注意,现在仍然在运行爬山算法的理论,仍然在判断最高的山头,也就是整体的跳跃还是趋于往最高处走的。但太活跃也不好,有可能随便一跳就把最优的山头跳过去了,这怎么办?没关系,这是退火算法,精髓在退火过程中。当物体加热到一定温度之后,开始退火,也就是降温,随着温度下降,粒子间运动减弱,也就是爬山人的的体力慢慢下降,此时跳跃能力减弱,有可能只能从山头跳到半山腰了。这个时候,由于体力下降了,但是在之前整体趋势还是往最高的山头走,那么在某个时刻,一定会找到最高的山头,并且在最高的山头上,跳不出去了(要知道,体力越下降,越跳不动)。直到物质温度降低到粒子间运动可以忽略不记的时候,此时爬山人可能累的只能步行了,此时整个算法就和爬山算法一样了,只能在最高的山头上找局部最优解(但作为最高的山头,局部最优解就是全局最优)。这就是模拟退火算法从退火过程中找到的理论基础。
上面的解释有个需要思考的地方,物质的粒子间运动能力,是由于温度变化引起的,那么爬山人的体力问题是靠什么引起的?时间?仔细想想这个问题就能发现模拟退火算法提出者的睿智之处。
下面部分讲解参考B站:数学建模清风第二次直播:模拟退火算法
模拟退火算法中的能力是靠随着时间变化得出的概率从而引起变化的,这句话可以分为两句。第一,靠概率引起变化;第二,概率随时间变化。模拟退火算法试想一下,若爬山人当前处于一个位置,往左走海拔变高,往右走海拔变低,但是通过计算得知,他下一步需要往右走若干米(往右走海拔变低),那么他要往右走么?如果你的答案是拒绝往右走,那么你使用的算法就是爬山算法了,你会大概率陷入局部最优。所以,正确答案是,以一定的概率接受这个结果,那么概率如何算?假设第一种情况:下一步的海拔与当前点的海拔相差无几;第二个情况:下一步的海拔与当前点的海拔相差巨大。你是不是更倾向于接受情况一。把海拔高度还原成函数值,即当前点的函数值(海拔值)f(A),以及下一步的函数值f(B),他俩的差值越小,你接受下一点的概率就越大。即 P 反 比 于 ∣ f ( A ) − f ( B ) ∣ P 反比于 |f(A)-f(B)| P反比于∣f(A)−f(B)∣但是,前面说了,这个爬山人的体力除了概率这一影响之外,还会有时间的影响的,所以此处直接 将 ∣ f ( A ) − f ( B ) ∣ ∗ C t 将|f(A)-f(B)|*Ct 将∣f(A)−f(B)∣∗CtCt就是时间常数。但是这不够,既然是模拟退火算法,那么少不了温度这个概念呀,于是,指鹿为马,直接给Ct改名为温度系数(此时注意P依然与|f(A)-f(B)|成反比)。那么问题又来了,时间是增长的,温度是下降的,于是只好放弃指鹿为马了,还是乖乖重新引入温度参数T吧。但是为了保证P与|f(A)-f(B)|成反比,那么只能把公式改为 P 反 比 于 ∣ f ( A ) − f ( B ) ∣ / T P反比于|f(A)-f(B)|/T P反比于∣f(A)−f(B)∣/TT是慢慢下降的,下降的步长一般取T*0.95。
还需要注意最后一个问题,既然称P为概率,那么怎么也得把P限制在0-1之间吧,但现在的P是0-正无穷,此时引入指数函数 P = e − ∣ f ( A ) − f ( B ) ∣ / T P = \ e^ {-|f(A)-f(B)|/T} \ P= e−∣f(A)−f(B)∣/T 那么现在P的范围在0-1之间了。
现在再重述一下公式,若两个函数值的差值不变,随着温度的下降,跳跃能力会变弱(看到这是不是想起来之前物质在退火过程中粒子间的运动了?),也就是概率P会减小,同样就是接受往下一步走的概率越小。若温度不变,两个函数值的差值越大,跳跃能力会变弱,也就是概率P会减小,同样就是接受往下一步走的概率越小。
下面给出模拟退火算法通用伪代码:
(1) 随机生成一个解A, 计算解A 对应的目标函数值f(A)
(2) 在A 附近随机生成一个解B,计算解B 对应的目标函数值f(B)
(3) 如果f(B)>f(A), 则将解B 赋值给解A,然后重复上面步骤(爬山法的思想);如果f(B)≤f(A), 那么我们计算接受B 的概率 P = e − ∣ f ( A ) − f ( B ) ∣ / T P = \ e^ {-|f(A)-f(B)|/T} \ P= e−∣f(A)−f(B)∣/T T为温度,然后我们生成一个[0,1]之间的随机数r,如果r2、路径规划算法伪代码
step1:建立地图
step2:随机生成一条可行路径,记作Old_path
step3:计算Old_path的适应度值,即从起点到终点的距离
step4:由Old_path路径生成一条新的路径,记作New_path
step5:计算New_path的适应度值
step6:判断两个路径的适应度值:
(a).如果New_path的适应度值小于Old_path的适应度值,则用New_path的路径信息更新Old_path的信息
(b).若New_path的适应度值大于Old_path的适应度值,则计算接受此条新路径的概率,称为接受概率。再随机产生一个0-1的随机数,若接受概率大于随机数,就用New_path的路径信息更新Old_path的信息,否则放弃New_path这条路径,还用Old_path路径进行搜索
step7:判断是否达到终止条件,若未达到,则循环3-6步骤,若达到,则停止程序,输出New_path的路径信息,并在地图上画出路径。三、算法流程及代码实现
1、地图创建
#step1 路径规划地图创建
class Map():
def __init__(self):
#10 是可行 白色
# 0 是障碍 黑色
# 8 是起点 颜色浅
# 2 是终点 颜色深
self.data = [[ 8,10,10,10,10,10,10,10,10,10],
[10,10, 0, 0,10,10,10, 0,10,10],
[10,10, 0, 0,10,10,10, 0,10,10],
[10,10,10,10,10, 0, 0, 0,10,10],
[10,10,10,10,10,10,10,10,10,10],
[10,10, 0,10,10,10,10,10,10,10],
[10, 0, 0, 0,10,10, 0, 0, 0,10],
[10,10, 0,10,10,10, 0,10,10,10],
[10,10, 0,10,10,10, 0,10,10,10],
[10,10,10,10,10,10,10,10,10, 2]]
plt.imshow(self.data, cmap=plt.cm.hot, interpolation='nearest', vmin=0, vmax=10)
# plt.colorbar()
xlim(-1, 10) # 设置x轴范围
ylim(-1, 10) # 设置y轴范围
my_x_ticks = np.arange(0, 10, 1)#刻度列表
my_y_ticks = np.arange(0, 10, 1)
plt.xticks(my_x_ticks)#画刻度
plt.yticks(my_y_ticks)
plt.grid(True)
plt.show()#显示
map = Map()#实例化 并显示地图
2、初始化路径
具体的操作方法为:
1、找到一条间断的路径,即从栅格图的每一行中随机取出一个不是障碍物的元素。这种操作在每一行中都取了一个元素,并且这些元素都是自由栅格,因此做完第一步之后得到的是一条间段路径。
2、将间断的路径连续化,在这步中,需要先从路径的第一个栅格节点判断与之相邻的下一个栅格节点是否为连续。
(1).若连续,迭代节点,判断下一个与之相邻的栅格节点。
(2).若不连续,那么采用中点插值法计算这两个栅格节点的中点。
a).若中点是自由栅格,就插入到当前路径中.
b).若中点不是自由栅格,那么进一步判断中点栅格周围8个邻域的栅格状态.
找到邻域中不是障碍的栅格,再插入到路径中。
若8个邻域都是障碍,那么说明这条路经没法进行连续化处理,也就是这条路行不通,此时删除这条路径,从1步骤再生成一条间隔路径,知道连续化完成。
代码如下:#step2 随机选取一个初始可行解
class FeasibleSolution():
def __init__(self):
self.p_start = 0 # 起始点序号0 10进制编码
self.p_end = 99 # 终点序号99 10进制编码
# self.xs = (self.p_start) // (self.col) # 行
# self.ys = (self.p_start) % (self.col) # 列
# self.xe = (self.p_end) // (self.col) # 终点所在的行
# self.ye = (self.p_end) % (self.col)
self.map = Map() # Map的实例化 主函数中可以不再初始化地图
# for i in range(10): #显示出来
# for j in range(10):
# print(self.map.data[i][j],end=' ')
# print('')
self.can = [] # 这个列表存放整个地图中不是障碍物的点的坐标 按行搜索
self.popu = []#缓存一下
self.end_popu = []#最终的
def feasiblesolution_init(self):
'''
:return:无返回值,随机选出一条初始可行解
'''
temp = []
while (temp == []):
self.end_popu = []
for xk in range(0,10): #遍历0-10行
self.can = [] #清空can列表 用来缓存当前行的可行点
for yk in range(0,10): #遍历所有的列
num = (yk) + (xk) * 10 #编码当前的坐标
if self.map.data[xk][yk] == 10: #可行点
self.can.append(num) #添加进can列表
# print(self.can,'自由点')
length = len(self.can) #此行的长度 随机生成指针取出坐标
# print(length)
a = (self.can[rd.randint(0, length - 1)])
self.end_popu.append(a) #在当前行的可行点中随机选一个给end_popu
self.end_popu[0] = self.p_start # 每一行的第一个元素设置为起点序号
self.end_popu[-1] = self.p_end #最后一个元素设为终点编号
# print('间段路径',self.end_popu)
temp = self.Generate_Continuous_Path(self.end_popu)#将返回的一条路经 添加进end中
# print('当前的路径',temp)
self.end_popu = fiter.fiter(temp) #滤除重复节点路径
# print(self.end_popu, end='\n')
# print('测试1',self.popu,end='\n')
return self.end_popu
# @staticmethod
def Generate_Continuous_Path(self,old_popu):#生成连续的路径个体
'''
:param old_popu: 未进行连续化的一条路径
:return: 无返回 # 已经连续化的一条路径
'''
num_insert = 0
self.new_popu = old_popu #传进来的参数就是一行的数组 一条路径
self.flag = 0
self.lengh = len(self.new_popu) #先将第一条路经的长度取出来
i = 0
# print("lengh =",self.lengh )
while i!= self.lengh-1: #i 不等于 当前行的长度减去1 从0计数 这里有问题 待修改
x_now = (self.new_popu[i]) // (10) # 行 解码 算出此条路经的第i个元素的直角坐标
y_now = (self.new_popu[i]) % (10) # 列
x_next = (self.new_popu[i+1]) // (10) #计算此条路经中下一个点的坐标
y_next = (self.new_popu[i+1]) % (10)
#最大迭代次数
max_iteration = 0
#判断下一个点与当前点的坐标是否连续 等于1 为连续
while max(abs(x_next - x_now), abs(y_next - y_now)) != 1:
x_insert = ((x_next + x_now) // 2) #行
y_insert = ((y_next + y_now) // 2) #ceil向上取整数 #列
# print("x_insert = ",x_insert,"\ty_insert = ",y_insert)
flag1 = 0
if self.map.data[x_insert][y_insert] == 10: #插入的这个坐标为10 可走
num_insert = (y_insert) + (x_insert) * 10 #计算出插入坐标的编码
self.new_popu.insert(i+1,num_insert)
# print(self.new_popu)
# print('插入编号',num_insert)
else:#插入的栅格为障碍 判断插入的栅格上下左右是否为障碍,以及是否在路径中,若不是障碍且不在路径中,就插入
#判断下方
if (x_insert + 1 < 10)and flag1 == 0: #保证坐标是在地图上的
if ((self.map.data[x_insert+1][y_insert] == 10)#下方不是障碍物
and (((y_insert) + (x_insert+1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert) + (x_insert+1) * 10 #计算下方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 #设置标志位 避免下面重复插入
# print('下方插入',num_insert)
#判断右下方
if (x_insert + 1 < 10)and (y_insert+1<10)and flag1 == 0: #保证坐标是在地图上的
if ((self.map.data[x_insert+1][y_insert+1] == 10)#下方不是障碍物
and (((y_insert+1) + (x_insert+1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert+1) + (x_insert+1) * 10 #计算下方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 #设置标志位 避免下面重复插入
# print('右下方插入',num_insert)
#判断右方
if (y_insert + 1 < 10)and flag1 == 0: # 保证坐标是在地图上的 并且前面没有插入
if ((self.map.data[x_insert][y_insert+1] == 10)#右方不是障碍物
and (((y_insert+1) + (x_insert) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert+1) + (x_insert) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('右方插入',num_insert)
#判断右上方
if (y_insert + 1 < 10)and (x_insert - 1 >= 0)and flag1 == 0: # 保证坐标是在地图上的 并且前面没有插入
if ((self.map.data[x_insert-1][y_insert+1] == 10)#右方不是障碍物
and (((y_insert+1) + (x_insert-1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert+1) + (x_insert-1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('右上方插入',num_insert)
#判断上方
if (x_insert - 1 >= 0) and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert-1][y_insert] == 10)#右方不是障碍物
and (((y_insert) + (x_insert-1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert) + (x_insert-1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('上方插入',num_insert)
#判断左上方
if (x_insert - 1 >=0) and(y_insert - 1 >= 0)and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert-1][y_insert-1] == 10)#右方不是障碍物
and (((y_insert-1) + (x_insert-1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert-1) + (x_insert-1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('左上方插入',num_insert)
#判断左方
if (y_insert - 1 >=0)and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert][y_insert-1] == 10)#右方不是障碍物
and (((y_insert-1) + (x_insert) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert-1) + (x_insert) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('左方插入',num_insert)
#判断左下方
if (y_insert - 1 >= 0)and(x_insert+1<10)and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert+1][y_insert-1] == 10)#右方不是障碍物
and (((y_insert-1) + (x_insert+1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert-1) + (x_insert+1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('左下方插入',num_insert)
if flag1 == 0: #如果前面没有插入新点 说明这条路径不对 删除
pass
# self.new_popu = []
# print(x_insert,y_insert,'没有可行点')
x_next = num_insert//10
y_next = num_insert%10
# x_next = x_insert
# y_next = y_insert
max_iteration += 1#迭代次数+1
if max_iteration > 20:
self.new_popu = [] #超出迭代次数 说明此条路经可能无法进行连续 删除路径
break
if self.new_popu == []:
# print('运行到这里2')
break
self.lengh = len(self.new_popu)
# print(self.new_popu, '连续,长度为:',self.lengh)
i = i+1
# print(self.new_popu,'连续')
return self.new_popu#返回的是一条路径
小结
但是在这里引发我一个思考,在遗传算法中初始化种群时,把连续不成功的路径丢弃是否合理?这种放弃会造成初始化种群规模与实际我需要的种群规模不一致。会影响后续的遗传操作。后续在遗传算法中加入这个while循环,以保证种群规模与实际需要一致,测试一下结果与之前相比是否会更加好。3、计算适应度值
代码如下:#step2 计算适应度函数
def calvalue(popu,col):
'''
:param popu: 传入单条路径信息
:param col: 这个参数是地图的列数 ,因为要解码用到
:return: 返回的是一个路径长度值
'''
value = 0 #存放计算出来的路径长度值
single_popu = popu
single_lengh = len(single_popu)#将当前行的长度拿出来
# print(single_lengh)
for j in range(single_lengh-1):#从第一个元素计算到倒数第一个元素
x_now = (single_popu[j]) // (col) # 行 解码 算出此条路经的第i个元素的直角坐标
y_now = (single_popu[j]) % (col) # 列
x_next = (single_popu[j + 1]) // (col) # 计算此条路经中下一个点的坐标
y_next = (single_popu[j + 1]) % (col)
if abs(x_now - x_next) + abs(y_now - y_next) == 1:#路径上下左右连续 不是对角的 则路径长度为1
value = value+1
elif max(abs(x_now - x_next),abs(y_now - y_next))>=2:#惩罚函数 若跳跃或者穿过障碍
value = value + 100
else:
value = value+1.4 #对角长度为根号2 即1.4
return value
4、5、产生新路径并计算适应度值
具体操作是:在前一条路径中随机找到除了起点和终点以外的另外两个栅格节点,然后将这两个栅格节点中间的路径全部删除,这样子就得到了一条间隔路径,再利用间隔路径连续化操作,使间隔路径连续,随之得到一条新的路径。产生新路径的代码如下:#step3 生成新的路径 采用遗传算法中变异的方法
def get_newsolution(oldsolution):
temp = [] # 定义一个缓存路径的空列表
while (temp == []):
single_popu = oldsolution
col = len(single_popu) # 长度 即列数 也就是这条路径有多少节点
first = rd.randint(1, col - 2) # 随机选取两个指针
second = rd.randint(1, col - 2)
if first != second: # 判断两个指针是否相同 不相同的话把两个指针中间的部分删除 在进行连续化
# 判断一下指针大小 便于切片
if (first < second):
single_popu = single_popu[0:first] + single_popu[second + 1:]
else:
single_popu = single_popu[0:second] + single_popu[first + 1:]
temp = feasiblesolution.Generate_Continuous_Path(single_popu) # 连续化
new_popu = (temp)
return new_popu
6、判断是否接受新路径
这里就是用到了模拟退火算法的精髓,接受概率,也就是前文提到的 P = e − ∣ f ( A ) − f ( B ) ∣ / T P = \ e^ {-|f(A)-f(B)|/T} \ P= e−∣f(A)−f(B)∣/T 直接将新路径长度与原始路径长度的差值代入公式,然后把当前的温度值也代入公式,就可以计算出当前接受新路径的概率,此时随机生成一个0-1的概率R,若P>R,则接受新路径,否则拒绝新路径,依旧使用原始路径。需要注意,在同一个温度下需进行多次搜寻。
判断的代码在主函数中,主函数如下所示:if __name__ == '__main__':
#参数初始化
T0 = 100 # 初始温度
T = T0 # 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 100 # 最大迭代次数
Lk = 100 # 每个温度下的迭代次数
alfa = 0.95 # 温度衰减系数
starttime = time.time()
print('开始时间:',starttime)
feasiblesolution = FeasibleSolution()
#step1随机产生一条路径信息
oldsolution = feasiblesolution.feasiblesolution_init()
print('初始路径',oldsolution)
old_value = calvalue(oldsolution, 10)
print('初始路径距离',old_value)
for i in range(maxgen): #外循环 迭代次数
for j in range(Lk): #内循环 每个温度下迭代的次数
#step2计算当前路径的适应度值
old_value = calvalue(oldsolution,10)
# print('当前适应度值',value)
#step3根据初始路径,生成新的路径
newsolution = get_newsolution(oldsolution)
# print('新的路径',newsolution)
new_value = calvalue(newsolution,10)
# print('新路径适应度值',new_value)
if new_value<=old_value: #新可行解的适应度值小于旧的 替换掉旧的
oldsolution = newsolution #更新路径
else:
p = np.exp(-(new_value-old_value)/T) #计算概率
if rd.random()<p:
oldsolution = newsolution #更新路径
T = T*alfa #温度下降
print('最终路径', oldsolution)
old_value = calvalue(oldsolution, 10)
print('最终路径距离',old_value)
stoptime = time.time() # 结束时间
print('结束时间:', stoptime)
print('共用时', stoptime - starttime, '秒')
for i in oldsolution:
if i == 0 or i ==99:
pass
else:
x = (i) // 10 # 行 解码 算出此条路经的第i个元素的直角坐标
y = (i) % 10 # 列
feasiblesolution.map.data[x][y] = 5 # 将路径用3表示
plt.imshow(feasiblesolution.map.data, cmap=plt.cm.hot, interpolation='nearest', vmin=0, vmax=10)
# plt.colorbar()
xlim(-1, 10) # 设置x轴范围
ylim(-1, 10) # 设置y轴范围
my_x_ticks = np.arange(0, 10, 1)
my_y_ticks = np.arange(0, 10, 1)
plt.xticks(my_x_ticks)
plt.yticks(my_y_ticks)
plt.grid(True)
plt.show()
7、输出结果
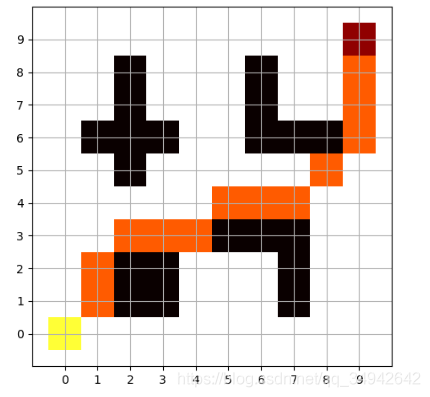

四、代码总工程
# -*- coding: UTF-8 -*-
'''*******************************
@ 开发人员:Mr.Zs
@ 开发时间:2020/5/24-14:27
@ 开发环境:PyCharm
@ 项目名称:算法类总工程->模拟退火算法路径规划V1.0.py
******************************'''
import numpy as np
import random as rd
import time
from pylab import *
import math
#这个对象专门滤除路径中的回头路
class Fiter:
def __init__(self):
self.b = 1 # 标志位
def function(self, a): # 定义一个函数
for i in a: # 遍历列表中的内容
a = a[a.index(i) + 1:] # 把当前内容索引的后面的内容剪切下来 因为前面的已经比对过了
if i in a: # 如果当前内容与后面有重复
return i, 1 # 返回当前重复的内容 以及标志位1
else: # 没有重复就不用管 继续for循环
pass
return 0, 0 # 全部遍历完 没有重复的就返回0 这里返回两个0 是因为返回的数量要保持一致
def fiter(self, a):
if a == []: #判断传进来的列表是否为空,空的话会报错 也没有必要进行下一步
return a
while (self.b == 1): # 标志位一直是 1 则说明有重复的内容
(i, self.b) = self.function(a) # 此时接受函数接收 返回值 i是重复的内容 b是标志位
c = [j for j, x in enumerate(a) if x == i] # 将重复内容的索引全部添加进c列表中
a = a[0:c[0]] + a[c[-1]:] # a列表切片在重组
return a
fiter = Fiter()#实例化对象
#step1
#生成的地图为指定大小的随机障碍地图
# class Map():
# '''
# :param:地图类
# :param:使用时需要传入行列两个参数 再实例化
# '''
#
# def __init__(self,row,col):
# '''
# :param:row::行
# :param:col::列
# '''
# self.data = []
# self.row = row
# self.col = col
# def map_init(self):
# '''
# :param:创建栅格地图row行*col列 的矩阵
# '''
# self.data = [[10 for i in range(self.col)] for j in range(self.row)]
# # for i in range(self.row):
# # for j in range(self.col):
# # print(self.data[i][j],end=' ')
# # print('')
# def map_Obstacle(self,num):
# '''
# :param:num:地图障碍物数量
# :return:返回包含障碍物的地图数据
# '''
# self.num = num
# for i in range(self.num):#生成小于等于num个障碍
# self.data[random.randint(0,self.row-1)][random.randint(0,self.col-1)] = 0
# if self.data[0][0] == 1: #判断顶点位置是否是障碍 若是 修改成可通行
# self.data[0][0] = 0
#
# if self.data[self.row-1][0] == 1:
# self.data[self.row-1][0] = 0
#
# if self.data[0][self.col-1] == 1:
# self.data[0][self.col - 1] = 0
#
# if self.data[self.row-1][self.col - 1] == 1:
# self.data[self.row - 1][self.col - 1] = 0
# for i in range(self.row): #显示出来
# for j in range(self.col):
# print(self.data[i][j],end=' ')
# print('')
# return self.data
#step1 路径规划地图创建
class Map():
def __init__(self):
#10 是可行 白色
# 0 是障碍 黑色
# 8 是起点 颜色浅
# 2 是终点 颜色深
self.data = [[ 8,10,10,10,10,10,10,10,10,10],
[10,10, 0, 0,10,10,10, 0,10,10],
[10,10, 0, 0,10,10,10, 0,10,10],
[10,10,10,10,10, 0, 0, 0,10,10],
[10,10,10,10,10,10,10,10,10,10],
[10,10, 0,10,10,10,10,10,10,10],
[10, 0, 0, 0,10,10, 0, 0, 0,10],
[10,10, 0,10,10,10, 0,10,10,10],
[10,10, 0,10,10,10, 0,10,10,10],
[10,10,10,10,10,10,10,10,10, 2]]
# for i in range(10): #显示出来
# for j in range(10):
# print(self.data[i][j],end=' ')
# print('')
#step2 随机选取一个初始可行解
class FeasibleSolution():
def __init__(self):
self.p_start = 0 # 起始点序号0 10进制编码
self.p_end = 99 # 终点序号99 10进制编码
# self.xs = (self.p_start) // (self.col) # 行
# self.ys = (self.p_start) % (self.col) # 列
# self.xe = (self.p_end) // (self.col) # 终点所在的行
# self.ye = (self.p_end) % (self.col)
self.map = Map() # Map的实例化 主函数中可以不再初始化地图
# for i in range(10): #显示出来
# for j in range(10):
# print(self.map.data[i][j],end=' ')
# print('')
self.can = [] # 这个列表存放整个地图中不是障碍物的点的坐标 按行搜索
self.popu = []#缓存一下
self.end_popu = []#最终的
def feasiblesolution_init(self):
'''
:return:无返回值,随机选出一条初始可行解
'''
temp = []
while (temp == []):
self.end_popu = []
for xk in range(0,10): #遍历0-10行
self.can = [] #清空can列表 用来缓存当前行的可行点
for yk in range(0,10): #遍历所有的列
num = (yk) + (xk) * 10 #编码当前的坐标
if self.map.data[xk][yk] == 10: #可行点
self.can.append(num) #添加进can列表
# print(self.can,'自由点')
length = len(self.can) #此行的长度 随机生成指针取出坐标
# print(length)
a = (self.can[rd.randint(0, length - 1)])
self.end_popu.append(a) #在当前行的可行点中随机选一个给end_popu
self.end_popu[0] = self.p_start # 每一行的第一个元素设置为起点序号
self.end_popu[-1] = self.p_end #最后一个元素设为终点编号
# print('间段路径',self.end_popu)
temp = self.Generate_Continuous_Path(self.end_popu)#将返回的一条路经 添加进end中
# print('当前的路径',temp)
self.end_popu = fiter.fiter(temp) #滤除重复节点路径
# print(self.end_popu, end='\n')
# print('测试1',self.popu,end='\n')
return self.end_popu
# @staticmethod
def Generate_Continuous_Path(self,old_popu):#生成连续的路径个体
'''
:param old_popu: 未进行连续化的一条路径
:return: 无返回 # 已经连续化的一条路径
'''
num_insert = 0
self.new_popu = old_popu #传进来的参数就是一行的数组 一条路径
self.flag = 0
self.lengh = len(self.new_popu) #先将第一条路经的长度取出来
i = 0
# print("lengh =",self.lengh )
while i!= self.lengh-1: #i 不等于 当前行的长度减去1 从0计数 这里有问题 待修改
x_now = (self.new_popu[i]) // (10) # 行 解码 算出此条路经的第i个元素的直角坐标
y_now = (self.new_popu[i]) % (10) # 列
x_next = (self.new_popu[i+1]) // (10) #计算此条路经中下一个点的坐标
y_next = (self.new_popu[i+1]) % (10)
#最大迭代次数
max_iteration = 0
#判断下一个点与当前点的坐标是否连续 等于1 为连续
while max(abs(x_next - x_now), abs(y_next - y_now)) != 1:
x_insert = ((x_next + x_now) // 2) #行
y_insert = ((y_next + y_now) // 2) #ceil向上取整数 #列
# print("x_insert = ",x_insert,"\ty_insert = ",y_insert)
flag1 = 0
if self.map.data[x_insert][y_insert] == 10: #插入的这个坐标为10 可走
num_insert = (y_insert) + (x_insert) * 10 #计算出插入坐标的编码
self.new_popu.insert(i+1,num_insert)
# print(self.new_popu)
# print('插入编号',num_insert)
else:#插入的栅格为障碍 判断插入的栅格上下左右是否为障碍,以及是否在路径中,若不是障碍且不在路径中,就插入
#判断下方
if (x_insert + 1 < 10)and flag1 == 0: #保证坐标是在地图上的
if ((self.map.data[x_insert+1][y_insert] == 10)#下方不是障碍物
and (((y_insert) + (x_insert+1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert) + (x_insert+1) * 10 #计算下方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 #设置标志位 避免下面重复插入
# print('下方插入',num_insert)
#判断右下方
if (x_insert + 1 < 10)and (y_insert+1<10)and flag1 == 0: #保证坐标是在地图上的
if ((self.map.data[x_insert+1][y_insert+1] == 10)#下方不是障碍物
and (((y_insert+1) + (x_insert+1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert+1) + (x_insert+1) * 10 #计算下方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 #设置标志位 避免下面重复插入
# print('右下方插入',num_insert)
#判断右方
if (y_insert + 1 < 10)and flag1 == 0: # 保证坐标是在地图上的 并且前面没有插入
if ((self.map.data[x_insert][y_insert+1] == 10)#右方不是障碍物
and (((y_insert+1) + (x_insert) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert+1) + (x_insert) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('右方插入',num_insert)
#判断右上方
if (y_insert + 1 < 10)and (x_insert - 1 >= 0)and flag1 == 0: # 保证坐标是在地图上的 并且前面没有插入
if ((self.map.data[x_insert-1][y_insert+1] == 10)#右方不是障碍物
and (((y_insert+1) + (x_insert-1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert+1) + (x_insert-1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('右上方插入',num_insert)
#判断上方
if (x_insert - 1 >= 0) and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert-1][y_insert] == 10)#右方不是障碍物
and (((y_insert) + (x_insert-1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert) + (x_insert-1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('上方插入',num_insert)
#判断左上方
if (x_insert - 1 >=0) and(y_insert - 1 >= 0)and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert-1][y_insert-1] == 10)#右方不是障碍物
and (((y_insert-1) + (x_insert-1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert-1) + (x_insert-1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('左上方插入',num_insert)
#判断左方
if (y_insert - 1 >=0)and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert][y_insert-1] == 10)#右方不是障碍物
and (((y_insert-1) + (x_insert) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert-1) + (x_insert) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('左方插入',num_insert)
#判断左下方
if (y_insert - 1 >= 0)and(x_insert+1<10)and flag1 == 0: # 保证坐标是在地图上的
if ((self.map.data[x_insert+1][y_insert-1] == 10)#右方不是障碍物
and (((y_insert-1) + (x_insert+1) * 10) not in self.new_popu)):#编号不在已知路径中
num_insert = (y_insert-1) + (x_insert+1) * 10 #计算右方的编号
self.new_popu.insert(i + 1, num_insert) #插入编号
flag1 = 1 # 设置标志位 避免下面重复插入
# print('左下方插入',num_insert)
if flag1 == 0: #如果前面没有插入新点 说明这条路径不对 删除
pass
# self.new_popu = []
# print(x_insert,y_insert,'没有可行点')
x_next = num_insert//10
y_next = num_insert%10
# x_next = x_insert
# y_next = y_insert
max_iteration += 1#迭代次数+1
if max_iteration > 20:
self.new_popu = [] #超出迭代次数 说明此条路经可能无法进行连续 删除路径
break
if self.new_popu == []:
# print('运行到这里2')
break
self.lengh = len(self.new_popu)
# print(self.new_popu, '连续,长度为:',self.lengh)
i = i+1
# print(self.new_popu,'连续')
return self.new_popu#返回的是一条路径
#step2 计算适应度函数
def calvalue(popu,col):
'''
:param popu: 传入单条路径信息
:param col: 这个参数是地图的列数 ,因为要解码用到
:return: 返回的是一个路径长度值
'''
value = 0 #存放计算出来的路径长度值
single_popu = popu
single_lengh = len(single_popu)#将当前行的长度拿出来
# print(single_lengh)
for j in range(single_lengh-1):#从第一个元素计算到倒数第一个元素
x_now = (single_popu[j]) // (col) # 行 解码 算出此条路经的第i个元素的直角坐标
y_now = (single_popu[j]) % (col) # 列
x_next = (single_popu[j + 1]) // (col) # 计算此条路经中下一个点的坐标
y_next = (single_popu[j + 1]) % (col)
if abs(x_now - x_next) + abs(y_now - y_next) == 1:#路径上下左右连续 不是对角的 则路径长度为1
value = value+1
elif max(abs(x_now - x_next),abs(y_now - y_next))>=2:#惩罚函数 若跳跃或者穿过障碍
value = value + 100
else:
value = value+1.4 #对角长度为根号2 即1.4
return value
#step3 生成新的路径 采用遗传算法中变异的方法
def get_newsolution(oldsolution):
temp = [] # 定义一个缓存路径的空列表
while (temp == []):
single_popu = oldsolution
col = len(single_popu) # 长度 即列数 也就是这条路径有多少节点
first = rd.randint(1, col - 2) # 随机选取两个指针
second = rd.randint(1, col - 2)
if first != second: # 判断两个指针是否相同 不相同的话把两个指针中间的部分删除 在进行连续化
# 判断一下指针大小 便于切片
if (first < second):
single_popu = single_popu[0:first] + single_popu[second + 1:]
else:
single_popu = single_popu[0:second] + single_popu[first + 1:]
temp = feasiblesolution.Generate_Continuous_Path(single_popu) # 连续化
new_popu = (temp)
return new_popu
if __name__ == '__main__':
#参数初始化
T0 = 10 # 初始温度
T = T0 # 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 100 # 最大迭代次数
Lk = 100 # 每个温度下的迭代次数
alfa = 0.95 # 温度衰减系数
starttime = time.time()
print('开始时间:',starttime)
feasiblesolution = FeasibleSolution()
#step1随机产生一条路径信息
oldsolution = feasiblesolution.feasiblesolution_init()
print('初始路径',oldsolution)
old_value = calvalue(oldsolution, 10)
print('初始路径距离',old_value)
for i in range(maxgen): #外循环 迭代次数
for j in range(Lk): #内循环 每个温度下迭代的次数
#step2计算当前路径的适应度值
old_value = calvalue(oldsolution,10)
# print('当前适应度值',value)
#step3根据初始路径,生成新的路径
newsolution = get_newsolution(oldsolution)
# print('新的路径',newsolution)
new_value = calvalue(newsolution,10)
# print('新路径适应度值',new_value)
if new_value<=old_value: #新可行解的适应度值小于旧的 替换掉旧的
oldsolution = newsolution #更新路径
else:
p = np.exp(-(new_value-old_value)/T) #计算概率
if rd.random()<p:
oldsolution = newsolution #更新路径
T = T*alfa #温度下降
print('最终路径', oldsolution)
old_value = calvalue(oldsolution, 10)
print('最终路径距离',old_value)
stoptime = time.time() # 结束时间
print('结束时间:', stoptime)
print('共用时', stoptime - starttime, '秒')
for i in oldsolution:
if i == 0 or i ==99:
pass
else:
x = (i) // 10 # 行 解码 算出此条路经的第i个元素的直角坐标
y = (i) % 10 # 列
feasiblesolution.map.data[x][y] = 5 # 将路径用3表示
plt.imshow(feasiblesolution.map.data, cmap=plt.cm.hot, interpolation='nearest', vmin=0, vmax=10)
# plt.colorbar()
xlim(-1, 10) # 设置x轴范围
ylim(-1, 10) # 设置y轴范围
my_x_ticks = np.arange(0, 10, 1)
my_y_ticks = np.arange(0, 10, 1)
plt.xticks(my_x_ticks)
plt.yticks(my_y_ticks)
plt.grid(True)
plt.show()
五、结束语