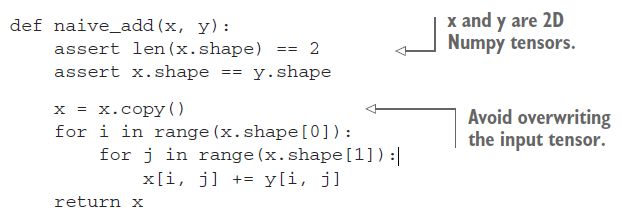深度学习

转载：https://www.jianshu.com/p/ba51e470b736

理解深度学习需要熟悉许多简单的数学概念:张量、张量运算、微分、梯度下降等等。
我们在这一章的目标将是建立你对这些概念的直觉，而不是过于技术性。特别地，我们将避开数学符号，对于那些没有任何数学背景的人来说，数学符号可能会令人不快，而且严格地说，数学符号对于很好地解释事情并非必需的。
为了增加张量和梯度下降的上下文，我们将从一个神经网络的实际例子开始这一章。然后我们会复习介绍过的每一个新概念。请记住，这些概念对于您理解接下来几章中的实际示例是非常重要的!阅读完这一章后，你将对神经网络的工作原理有一个直观的了解，你将能够进入实际应用——从第3章开始。

---

2.1 神经网络一瞥

让我们来看一个神经网络的具体例子，它使用Python库Keras来学习如何对手写数字进行分类。除非您已经有过Keras或类似库的经验，否则您不会立即理解第一个示例的全部内容。您可能还没有安装Keras;这很好。在下一章中，我们将回顾示例中的每个元素并详细解释它们。所以，如果有些步骤看起来很随意或者看起来很神奇，不要担心!我们总得有个开始。
我们试图解决的问题是对灰度图像进行分类的手写数字(28×28个像素)到他们的10个分类(0到9)。我们将使用MNIST数据集,一个机器学习社区中的经典,它的存在时间几乎与该领域本身一样长，并且已经得到了深入的研究。这是一套6万张训练图像，加上1万张测试图像——你要做的就是验证你的算法。你可以把“解决”MNIST看作深度学习的“Hello World”—您要做的就是验证您的算法是否按照预期工作。当你成为一个机器学习的实践者，你会看到MNIST一遍又一遍地出现在科学论文、博客帖子等等上。您可以在图2.1中看到一些MNIST示例。

• 分类和标签上的注意点
  在机器学习中，分类问题中的一个类别称为类。数据点称为样本。与特定样本关联的类称为标签。

 

您现在不需要在您的机器上复制这个示例。如果您愿意，您首先需要设置Keras，它将在3.3节中介绍。
MNIST数据集以Keras的形式预先加载，形式是4个Numpy数组。
train_images和train_label构成了训练集，即模型将从中学习的数据。然后将在测试集，即test_images和test_label上测试模型。

Listing 2.1 Loading the MNIST dataset in Keras

from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

图像被编码为Numpy数组，标签是一个数字数组，范围从0到9。图像和标签有一对一的对应关系。
让我们看看培训数据:

>>> train_images.shape
(60000, 28, 28)
>>> len(train_labels)
60000
>>> train_labels
array([5, 0, 4, ..., 5, 6, 8], dtype=uint8)

下面是测试数据:

>>> test_images.shape
(10000, 28, 28)
>>> len(test_labels)
10000
>>> test_labels
array([7, 2, 1, ..., 4, 5, 6], dtype=uint8)

工作流程如下:首先，我们将向神经网络提供训练数据、train_images和train_label。然后，该网络将学会关联图像和标签。最后，我们将要求网络为test_images生成预测，并验证这些预测是否与test_label中的标签匹配。
让我们构建网络—同样地，记住您还没有被期望了解关于这个示例的所有内容。

Listing 2.2 The network architecture

from keras import models
from keras import layers
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))

神经网络的核心构件是层，这是一个数据处理模块，你可以把它看作是数据的过滤器。一些数据输入，然后以更有用的形式输出。具体来说，层从提供给它们的数据中提取表示——希望这些表示对手边的问题更有意义。大多数深度学习都是将简单的层链接在一起，从而实现一种渐进式数据精馏的形式。深度学习模型就像一个数据处理的筛子，由一系列不断改进的数据过滤器层组成。
在这里，我们的网络由两个密集层（Dense layers）组成，它们紧密连接(也称为完全连接)神经层。第二个(也是最后一个)层是10路softmax层，这意味着它将返回一个包含10个概率分数的数组(总和为1)，每个分数都将是当前数字图像属于我们的10个分类之一的概率。
为了使网络为训练做好准备，我们需要再选择三样东西，作为编译步骤的一部分:

• 损失函数： 网络如何能够测量它在训练数据上的表现，如何能够引导自己走向正确的方向
• 优化器：网络根据所接收的数据及其损失函数进行自我更新的机制
• 在训练和测试期间监控的指标：这里，我们只关心准确性(正确分类的图像的一部分)。

损失函数和优化器的确切用途将在接下来的两章中明确。

Listing 2.3 The compilation step

network.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])

在训练之前，我们将对数据进行预处理，方法是将其重新塑造成网络期望的形状，并对其进行缩放，使所有值都位于[0,1]区间。例如，以前，我们的训练图像存储在uint8类型的形状数组(60000,28,28)中，值在[0,255]区间。我们将其转换为一个浮点32的形状数组(60000,28 * 28)，值介于0和1之间。

Listing 2.4 Preparing the image data

train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

我们还需要对标签进行分类编码，这一步将在第三章中解释。

Listing 2.5 Preparing the labels

from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)

我们现在已经准备好训练这个网络，在Keras中是通过调用网络的匹配（fit）方法来完成的——我们将模型与它的训练数据相匹配（fit）:

>>> network.fit(train_images, train_labels, epochs=5, batch_size=128)
Epoch 1/5
60000/60000 [==============================] - 9s - loss: 0.2524 - acc: 0.9273
Epoch 2/5
51328/60000 [========================>.....] - ETA: 1s - loss: 0.1035 - acc: 0.9692

在训练过程中显示两个量:网络在训练数据上的损失，以及网络在训练数据上的准确性。
我们在训练数据上的准确率很快达到了0.989(98.9%)。现在让我们检查模型在测试集上的表现是否良好:

>>> test_loss, test_acc = network.evaluate(test_images, test_labels)
>>> print('test_acc:', test_acc)
test_acc: 0.9785

测试集的准确率是97.8%，比训练集的准确率要低很多。训练精度和测试精度之间的差距是过度拟合的一个例子:机器学习模型在新数据上的表现往往比在训练数据上的表现差。过度拟合是第三章的中心话题。
这就是我们的第一个示例—您刚刚看到了如何构建和训练一个神经网络，以便在少于20行Python代码中对手写数字进行分类。在下一章中，我将详细介绍我们刚刚预览过的每一个移动的片段，并阐明幕后发生的事情。你会学到张量，网络中的数据存储对象;张量运算（这些层是由张量运算构成的)和梯度下降(这允许你的网络学习它的训练样例)。

2.2 神经网络的数据表示

在前面的示例中，我们从存储在多维数据数组(也称为张量)中的数据开始。一般来说，目前所有的机器学习系统都使用张量作为基本的数据结构。张量是该领域的基本，以至于谷歌的TensorFlow就是以它们命名的。什么是张量?
在其核心，张量是数据的容器——几乎总是数值数据。它是数字的容器。你可能已经熟悉矩阵了，它们是二维张量:张量是矩阵在任意维数下的推广(注意，在张量的上下文中，维度通常称为轴)。

2.2.1 标量（0维张量）

只有一个数字的张量叫做标量(或者标量张量，或者0维张量，或者0D张量)。在Numpy中，浮点32或浮点64的数字是标量张量(或标量数组)。可以通过ndim属性显示一个Numpy张量的轴数;标量张量有0个轴(ndim == 0)，一个张量的轴数也叫它的秩。这里有一个Numpy标量:

>>> import numpy as np
>>> x = np.array(12)
>>> x
array(12)
>>> x.ndim
0

2.2.2 向量（1维张量）

一个数字数组称为向量，或1D张量。一维张量据说只有一个轴。下面是一个Numpy向量:

>>> x = np.array([12, 3, 6, 14])
>>> x
array([12, 3, 6, 14])
>>> x.ndim
1

这个向量有五个分量，所以叫做5维向量。不要混淆5D向量和5D张量!一个5D矢量只有一个轴，沿着它的轴有五个维度，而一个5D张量有五个轴(每个轴上可能有任意多个维度)。维数可以表示沿某一特定轴的分量数(如5D向量)或张量(如a)中的轴数，这有时会让人困惑。在后一种情况下，从技术上来说，讨论一个秩为5的张量(张量的秩是轴的数目)更正确，但是不管怎样，5D张量的模糊符号都很常见。

2.2.3 矩阵

向量组成的数组是一个矩阵，或者说是二维张量。矩阵有两个轴(通常指行和列)。你可以直观地把矩阵解释成一个矩形的数字网格。
这是一个数字矩阵:

>>> x = np.array([[5, 78, 2, 34, 0],
                  [6, 79, 3, 35, 1],
                  [7, 80, 4, 36, 2]])
>>> x.ndim
2

来自第一个轴的条目称为行，来自第二个轴的条目称为列。在前面的例子中，[5,78,2,34,0]是x的第一行，[5,6,7]是第一列。

2.2.4 3D张量与高维张量

如果你把这些矩阵打包成一个新的数组，你会得到一个三维张量，你可以直观地把它解释为一个数字的立方。下面是一个Numpy 3D张量:

>>> x = np.array([[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]]])
>>> x.ndim
3

通过将三维张量填充到一个数组中，就可以创建一个4D张量，以此类推。在深度学习中，你通常会操作0到4D的张量，尽管当你处理视频数据，你可能会上升到5D。

2.2.5 关键属性

张量通过三个关键属性来定义

• 轴数(秩)——例如，一个三维张量有三个轴，一个矩阵有两个轴。这在Python库(如Numpy)中也称为张量的ndim。
• 形状——这是一个整数的元组，它描述了张量沿着每个轴有多少维。例如，前面的矩阵示例有shape(3,5)，三维张量的例子有形状(3,3,5)，向量的形状只有一个元素，例如(5，)，而标量的形状是空的，()。
• 数据类型(通常在Python库中称为dtype)——这是张量中包含的数据类型;例如，张量的类型可以是float32, uint8, float64等等。在很少的情况下，你可能会看到一个char张量。注意，字符串张量不存在于Numpy中(或在大多数其他库中)，因为张量存在于预先分配的、连续的内存段中:而字符串是可变长度的，因此不能使用这个实现。
  为了使这更具体，让我们回顾一下在MNIST示例中处理的数据。首先，我们加载MNIST数据集

from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

接下来，我们显示张量train_images的轴数，ndim属性:

>>> print(train_images.ndim)
3

这是它的形状:

>>> print(train_images.shape)
(60000, 28, 28)

这是它的数据类型，dtype属性

>>> print(train_images.dtype)
uint8

这里是一个8-bit整数的三维张量。更准确地说，它是一个数组,拥有60000个28×28的整数值构成的矩阵。每个这样的矩阵是一个灰度图像，系数在0到255之间。
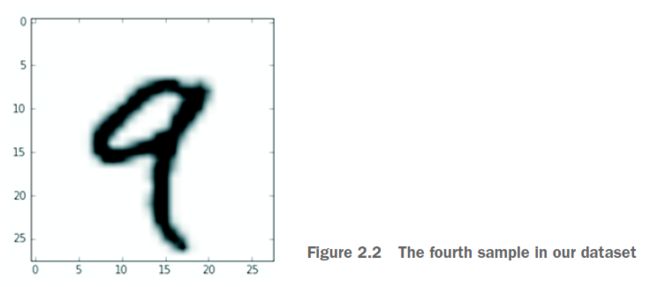
让我们使用Matplotlib库(标准科学Python套件的一部分)在这个3D张量中显示第四位数;参见图2.2。

Listing 2.6 Displaying the fourth digit

digit = train_images[4]
import matplotlib.pyplot as plt
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()

2.2.6 操作Numpy中的张量

在前面的示例中，我们使用语法train_images[i]在第一个轴旁边选择了一个特定的数字。在张量中选择特定的元素称为张量切片。
让我们看看在Numpy数组上可以执行的张量-切片操作(备注下：这里是Numpy的切片不是python的切片)。
下面的示例选择数字#10到#100(不包括#100)，并将它们放入一个形状为(90、28、28)的数组:

>>> my_slice = train_images[10:100]
>>> print(my_slice.shape)
(90, 28, 28)

它等价于这个更详细的符号，它指定沿着每个张量轴的切片的起始索引和终止索引。注意":"等于选择整个轴:

 

 

一般来说，你可以选择沿着每个张量轴的任意两个指标。例如,为了在右下角选择14×14像素的图像,你这样做:

my_slice = train_images[:, 14:, 14:]

也可以用负数指标。很像Python列表中的负数索引，它们表示相对于当前轴末端的位置。为了裁剪出在中心位置的14 × 14像素的图片，你可以这样子做：

my_slice = train_images[:, 7:-7, 7:-7]

2.2.7 数据分组的概念

一般来说，在深度学习中遇到的所有数据张量中，第一个轴(轴0，因为索引从0开始)是样本轴(有时称为样本维度)。在MNIST示例中，示例是数字图像。
此外，深度学习模型不会一次处理整个数据集;相反，他们把数据分成小组。具体来说，这是我们的一组MNIST数字，组大小128:

batch = train_images[:128]

这是下一批:

batch = train_images[128:256]

这是第n组：

batch = train_images[128 * n:128 * (n + 1)]

当考虑这样的分组张量时，第一个轴(轴0)称为分组轴（batch tensor）或分组维。在使用Keras和其他深度学习库时，您会经常遇到这个术语。

2.2.8 数据张量的实际例子

让我们用一些类似于您稍后将遇到的示例使数据张量更加具体。您将要操作的数据几乎总是属于以下类别之一:

• 向量数据: 2D张量的形状(样本、特征)
• 时间序列数据或序列数据：3D张量的形状(样本、timesteps,、特征)
• 图片：4D张量的形状（样本，高度，宽度，通道）或（样本，通道，高度，宽度）
• 视频：5D张量的形状(样品，帧（Frame），高度，宽度，通道)或（样本，帧（Frame），通道，高度，宽度）

2.2.9 向量数据

这是最常见的情况。在这样的数据集中，每个数据点都可以被编码为一个向量，因此一批数据将被编码为一个二维张量(即向量数组)，其中第一轴是样本轴，第二轴是特征轴。
让我们来看两个例子:

• 人的保险精算数据集，其中我们考虑每个人的年龄，邮政编码和收入。每个人都可以被描述为3个值的向量，因此一个10万人的完整数据集可以以二维形状张量的形式存储(100000,3)。
• 文本文档的数据集，其中我们用每个单词出现的次数(从20,000个常用单词的字典中)来表示每个文档。每个文档都可以被编码为20,000个值的向量(字典中每个单词有一个计数)，因此，一个包含500个文档的完整数据集可以以一个形状张量(500,20000)存储。

2.2.10 时间序列数据或序列数据

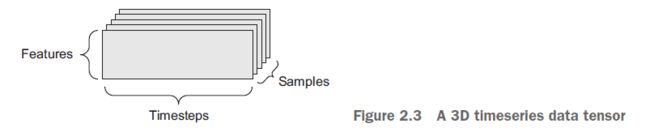
无论何时在数据中时间很重要(或者序列顺序的概念)，将它存储在一个带有明确时间轴的3D张量中都是有意义的。每个样本都可以编码为向量序列(一个2D张量)，因此一批数据将被编码为一个3D张量(见图2.3)。

 

 

按照惯例，时间轴总是第二个轴(索引1的轴)。让我们来看几个例子:

• 股票价格的数据集。每一分钟，我们存储当前的股票价格，在过去一分钟的最高的价格与最低的价格。因此，每一分钟都被编码为一个3D向量，一天的交易被编码为一个二维形状张量(390,3)(一个交易日有390分钟)，250天的数据可以存储在一个三维形状张量中(250，390, 3)。在这里，每个样本相当于一天的数据量。
• 一个tweet（推特）的数据集。其中我们将每个tweet编码为128个唯一字符的字母表中的280个字符序列。在这个设置中，每个字符都可以被编码为大小为128的二进制向量(除了对应字符的索引处的一个1项之外的全零向量)。然后将每条推文编码为二维形状张量(280,128)，将100万条推文的数据集存储为一个形状张量(1000000，280,128)。

2.2.11 图片数据

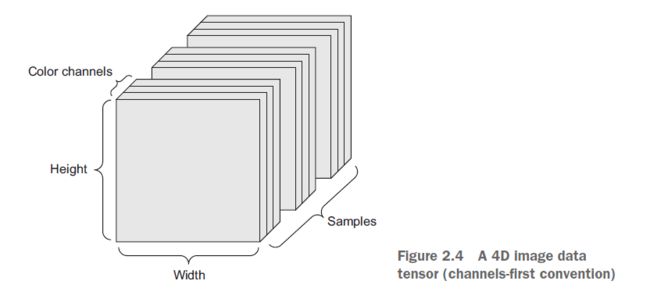
图像通常有三个维度:高度、宽度和颜色深度。虽然灰度图像(如我们的MNIST数字)只有一个颜色通道，因此可以存储在二维张量中，但按照惯例，图像张量总是3D的，灰度图像只有一个单向颜色通道。一批128灰度级图像大小为256×256，可以存储在一个形状张量(128、256、256、1),和一批128彩色图像可以存储在一个张量的形状(128、256、256、3)

 

 

对于图像张量的形状有两种约定:通道最后（channel-last）约定(由TensorFlow使用)和通道优先约定(由Theano使用)。来自Google的TensorFlow machine-learning framework将颜色深度轴放置在末尾:(sample, height, width, color_depth)。同时，Theano将颜色深度轴放置在分组处理轴的右侧:(sample, color_depth, height, width)。在Theano约定下，前面的示变为(128、1、256、256)和(128、3、256、256)。Keras框架提供了对这两种格式的支持。

2.2.12 视频数据

视频数据是现实世界中为数不多的需要5D张量的数据之一。一个视频可以理解为一系列的帧，每个帧都是一个彩色图像。因为每个帧可以存储在一个3D张量中(height, width, color_depth),，所以一串帧可以存储在一个4D张量中(frames, height, width, color_depth),，因此一批不同的视频可以存储在一个5D形状的张量中(samples, frames, height, width, color_depth).。
例如,一个60秒,144×256 YouTube视频采样4帧/每秒获得240帧。一组四段这样的视频片段将以张量的形式存储(4,240,144,256,3)，总共106,168,320个值!如果张量的dtype是float32，那么每个值都将存储在32位中，因此张量将表示405mb。您在现实生活中遇到的视频要轻得多，因为它们不存储在float32中，而且它们通常被一个大因素(如MPEG格式)压缩。

2.3 神经网络的齿轮：张量操作

就像任何计算机程序最终都可以简化为对二进制输入(和，或，NOR，等等)的一组二进制操作一样，深度神经网络学习到的所有转换都可以简化为应用于数字数据张量的少量张量操作。例如，可以加上张量，乘以张量，等等。
在我们的初始示例中，我们通过将密集层叠加在一起来构建网络。Keras层实例如下:

keras.layers.Dense(512, activation='relu')

这一层可以被解释为一个函数，它以一个二维张量作为输入，并返回另一个二维张量——一个输入张量的新表示。具体来说，函数如下(其中W为二维张量，b为向量，这两个都是层的属性):

output = relu(dot(W, input) + b)

让我们解释它。我们有三个张量运算:输入张量和一个叫W的张量之间的点积;在得到的二维张量和向量b之间加(+);最后是relu操作。relu(x)是max(x, 0)
注意： 尽管本节完全处理线性代数表达式，但在这里您不会找到任何数学符号。我发现，没有数学背景的程序员可以更容易地掌握数学概念，如果它们被表达为简短的Python代码片段，而不是数学方程。所以我们将自始至终使用Numpy代码。

2.3.1 元素级的操作

relu操作和加法操作是基于元素的操作:这些操作分别应用于所考虑的张量中的每个条目。这意味着这些操作非常适合大规模并行实现(矢量化实现，这个术语来自于1970-1990年期间的向量处理器超级计算机架构)。如果你想编写一个元素操作的简单Python实现，你可以使用for循环，就像这个元素操作的简单实现一样:

 

 

同样的执行加法操作：

 

根据相同的原理，可以按元素进行乘法、减法等等。
在实践中，当处理Numpy数组时，这些操作也可以使用优化后的内置Numpy函数，这些函数本身将繁重的工作委托给基本线性函数库的实现（(BLAS，如果您安装了）。BLAS是低层次的、高度并行的、高效的张量处理例程，通常在Fortran或C语言中实现。

因此，在Numpy中，您可以执行以下元素操作，并且它将非常快:

 

2.3.2 Broadcasting

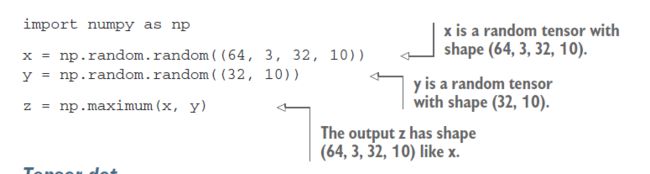
我们早期简单的naive_add实现只支持添加具有相同形状的2D张量。但是在前面介绍的致密层中，我们添加了一个二维张量和一个向量。当两个张量的形状不同时，加法会发生什么?
在可能的情况下，如果没有歧义，就会广播较小的张量来匹配较大张量的形状。广播包括两个步骤:

1. 将轴(称为广播轴)添加到较小的张量中，以匹配较大张量的ndim。

2. 较小的张量在这些新轴旁边重复，以匹配较大张量的完整形状。
   让我们来看一个具体的例子。考虑形状为(32,10)的X和形状为(10,)的y的情况。首先，我们向y增加一个空的第一轴，它的形状变成(1,10)。然后，我们沿着这个新轴重复y 32次，这样我们就得到了一个形状为(32,10)的张量Y，其中Y[i，:] == y for i in range(0, 32).。在这一点上，我们可以继续加X和Y，因为它们的形状是一样的。
   在实现方面，没有创建新的2D张量，因为那样会非常低效。重复操作完全是虚拟的:它发生在算法级别而不是内存级别。但是考虑向量在一个新的轴旁重复10次是一个有用的心理模型。下面是一个简单的实现:

    

   

    

   对于广播，如果一个有形状(a, b，…n, n + 1，…m)的张量，另一个有形状(n, n + 1，…m)，那么广播就会自动发生在a到n - 1的坐标轴上。
   下面的例子通过广播对两个不同形状的张量应用元素最大运算:

    

   

2.2.3 张量点运算

点运算，也被称为张量积(不要和元素积混淆)是最常见，最有用的张量运算。与元素操作相反，它将输入张量中的项组合在一起。
元素级的乘积是使用Numpy、Keras、Theano和和TensorFlow中的*操作符完成的。在Numpy和Keras使用标准dot运算符，而在TensorFlow中使用不同的语法.dot:

import numpy as np
z = np.dot(x, y)

在数学符号中，你通过一个点（.）完成点运算

z = x . y

数学上，点运算做什么?我们从两个向量x和y的点积开始，计算方法如下:

# x and y are Numpy vectors.
def naive_vector_dot(x, y):
    assert len(x.shape) == 1
    assert len(y.shape) == 1
    assert x.shape[0] == y.shape[0]
    z = 0.
    for i in range(x.shape[0]):
        z += x[i] * y[i]
    return z

你会注意到两个向量之间的点积是一个标量，只有元素个数相同的向量才能与点积相容。
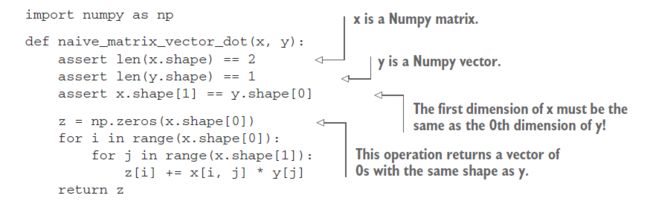
你也可以取矩阵x和向量y之间的点积，它返回一个向量，其中系数是y和x行之间的点积。

 

 

您还可以重用我们前面编写的代码，这突出显示了矩阵-向量积和向量积之间的关系

def naive_matrix_vector_dot(x, y):
    z = np.zeros(x.shape[0])
    for i in range(x.shape[0]):
        z[i] = naive_vector_dot(x[i, :], y)
    return z

注意，一旦两个张量中的一个ndim大于1，点就不再是对称的，也就是说点(x, y)不等于点(y, x)
当然，点积可以推广到带有任意数量轴的张量。
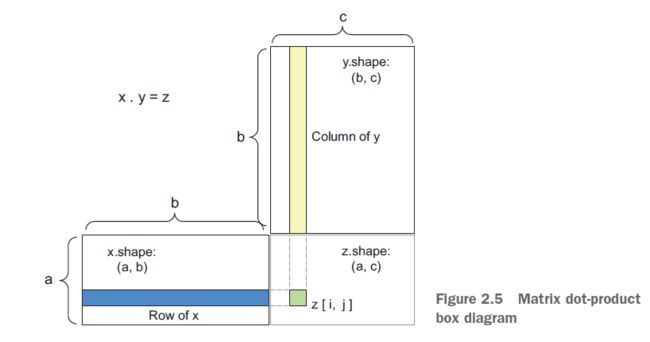
最常见的应用可能是两个矩阵之间的点积。你可以取两个矩阵x和y的点积(dot(x, y))当且仅当x.shape[1] == y.shape[0].。结果是一个形状为(x.shape[0]，y.shape[1])的矩阵。其中系数是x行和y列之间的向量乘积，下面是简单的实现方法:

 

 

为了理解点乘的形状兼容性，可以通过对齐输入和输出张量来帮助可视化，如图2.5所示。

 

x、y和z被描绘成矩形(系数的文本框)。由于y的行、x和列的大小必须相同，因此x的宽度必须与y的高度匹配。
更一般的情况下，你可以在高维张量之间取点积，遵循与之前二维情况相同的形状兼容性规则:

(a, b, c, d) . (d,) -> (a, b, c)
(a, b, c, d) . (d, e) -> (a, b, c, e)

2.3.4张量重构
第三种重要的张量运算是张量重构（reshaping）。虽然在我们的第一个神经网络示例中没有在密集层中使用它，但我们在将数字数据输入网络之前对其进行预处理时使用了它:

train_images = train_images.reshape((60000, 28 * 28))

重构一个张量意味着重新排列它的行和列以匹配目标形状。
自然地，重构张量的系数总数与初始张量相同。通过简单的例子最好地理解重塑：

>>> x = np.array([[0., 1.],
                 [2., 3.],
                 [4., 5.]])
>>> print(x.shape)
    (3, 2)
>>> x = x.reshape((6, 1))
>>> x
array([[ 0.],
[ 1.],
[ 2.],
[ 3.],
[ 4.],
[ 5.]])
>>> x = x.reshape((2, 3))
>>> x
array([[ 0., 1., 2.],
[ 3., 4., 5.]])

通常会遇到的一个特殊的重构案例是置换。变换矩阵意味着交换它的行和列，使x[i，:]变成x[:， i]:

# Creates an all-zeros matrix of shape (300, 20)
>>> x = np.zeros((300, 20)) 
>>> x = np.transpose(x)
>>> print(x.shape)
(20, 300)

2.3.5张量运算的几何表示

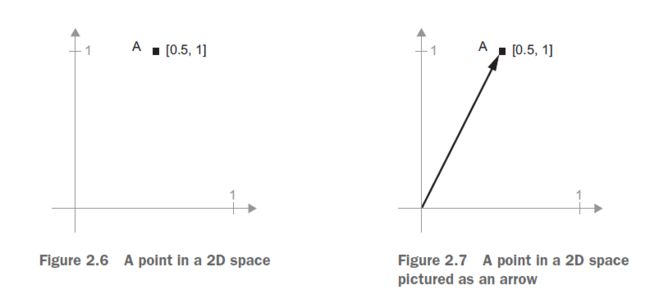
由于张量运算处理的张量的内容可以解释为某些几何空间中点的坐标，所以所有张量运算都有一个几何解释。例如，让我们考虑加法。我们从下面的向量开始:

A = [0.5, 1]

它是二维空间中的点(参见图2.6)。通常将向量画成一个箭头，将原点与点连接起来，如图2.7所示。

 

 

让我们考虑一个新的点，B =[1,25]，我们将把它加到前面的点上。这是通过将矢量箭头以几何方式连接在一起来实现的，生成的位置是表示前两个矢量之和的向量(见图2.8)。

 

一般来说，基本的几何运算，如仿射变换、旋转、缩放等，可以表示为张量运算。例如，2D向量旋转夹角θ可以通过一个2×2的矩阵点积R = [u, v]来实现。其中u和v都是该平面的向量：u = [cos(theta)， sin(theta)]和 v = [-sin(theta) cos(theta)]。（备注:就是旋转矩阵的概念）。

2.3.6深度学习的几何解释

你刚刚知道神经网络完全由张量运算链组成并且所有这些张量运算都是输入数据的几何变换。由此可见，您可以将神经网络解释为高维空间中非常复杂的几何变换，通过一系列简单的步骤实现。
在3D中，下面的图像可能会被证明是有用的。想象两张彩色纸:一张红的，一张蓝的。把一个放在另一个上面。现在把它们揉成一个小球。那个皱巴巴的纸球是你的输入数据，每一张纸都是一个分类问题中的一类数据。神经网络(或任何其他机器学习模型)想要做的是计算出纸球的一个变换，使它不皱，从而使这两个类再次干净地分离。通过深度学习，这将被实现为一系列简单的转换。

 

 

解皱纸球是机器学习的主题:为复杂的、高度折叠的数据流形找到整齐的表示形式。在这一点上,你应该有一个很好的直觉为什么深度学习擅长:需要增量的方法将一个复杂的几何变换分解为基本的长链,这几乎是人类可以按照这些策略解皱一个纸球。深层网络中的每一层都应用了一种转换，这种转换可以将数据稍微分离出来——而一层一层的堆叠，使易于处理成为一个极其复杂的解缠过程。

2.4 神经网络的引擎:基于梯度的优化

正如您在前一节中看到的，第一个网络示例中的每个神经层都将其输入数据转换为如下所示:

output = relu(dot(W, input) + b)

在这个表达式中，W和b是张量，它们是层的属性。它们被称为层的权值或可训练的参数(分别是内核和偏置属性)。
这些权重包含网络从暴露的训练数据中获得的信息。

2.5 回顾我们的第一个例子

最初，这些权重矩阵用小的随机值(称为随机初始化步骤)填充。当然，没有理由期望relu(dot(W，input)+ b)，当W和b是随机的，会产生任何有用的表示。结果的表示是无意义的，但它们是一个起点。接下来就是根据反馈信号逐步调整权重。这种渐进的调整，也叫训练，基本上就是机器学习的全部内容。
这发生在所谓的训练循环中，它的工作原理如下。在循环中重复这些步骤，只要有必要:

• 1. 绘制一批训练样本x和相应的目标y
• 1. 在x上运行网络(称为forward pass))以获得预测y_pred。
• 1. 计算批处理上的网络损失，这是y_pred和y之间不匹配的度量。
• 1. 更新网络的所有权重，以稍微减少这批的损失。

你最终会得到一个训练数据损耗非常低的网络:预测y_pred与预期目标y之间的不匹配度很低.网络已经“学会”将输入映射到正确的目标。从远处看，它可能看起来像魔法，但当你把它简化为基本步骤时，它就变得简单了。
第1步听起来很简单——只需输入/输出代码。第2步和第3步仅仅是少数张量运算的应用，所以您可以完全从上一节中学到的知识来实现这些步骤。最困难的部分是步骤4:更新网络的权重。给定网络中的单个权重系数，如何计算该系数是应该增加还是减少，增加了多少?
一个简单的解决方案是冻结网络中的所有权值，只考虑一个标量系数，并尝试对这个系数取不同的值。假设系数的初始值是0.3。对一批数据进行转发后，批数据上的网络损耗为0.5。如果将系数值更改为0.35并重新运行前传，损失将增加到0.6。但是如果你降低系数0.25，损失降到0.4。在这种情况下，似乎更新系数为-0.05将有助于减少损失。这必须对网络中的所有系数进行重复。
但是这样的方法会非常低效，因为你需要为每一个单独的系数计算两个forward passes(这是高代价的)(其中有很多，通常是几千，有时甚至是几百万)。一种更好的方法是利用网络中使用的所有操作都是可微的这一事实，并根据网络系数计算损失的梯度。然后你可以把系数从梯度方向移到相反的方向，从而减少损失。
如果你已经知道什么是可微的，什么是梯度，你可以跳到2.4.3节。否则，下面两个部分将帮助您理解这些概念。

2.4.1 导数是什么

考虑一个连续的平滑函数f(x) = y，将一个实数x映射到一个新的实数y，因为这个函数是连续的，x的一个小变化只能导致y的一个小变化，这就是连续性背后的直觉。假设将x增加一个小因子epsilon_x:这将导致epsilon_y变成y:

f(x + epsilon_x) = y + epsilon_y

另外，由于函数是光滑的(曲线没有任何急转弯)，当epsilon_x足够小，在某一点p附近，可以近似f为斜率a的线性函数，使epsilon_y变成 a * epsilon_x:

f(x + epsilon_x) = y + a * epsilon_x

显然，这个线性近似只有当x接近p时才有效。
斜率a称为f在p点的导数，如果a为负，则表示x在p附近的微小变化会导致f(x)的减小(如图2.10所示);如果a是正的，x的微小变化会导致f(x)的增加。此外，a的绝对值(导数的大小)告诉你增加或减少的速度。

 

 

对于每个可微函数f(x)(可微意味着“可导”:例如，光滑连续的函数可导)，存在一个导数函数f'(x)，它将x的值映射到这些函数中f的局部线性逼近的斜率。例如，cos(x)的导数是-sin(x)， f(x)的导数是f'(x) = a，以此类推。
如果你想通过因子epsilon_x减少f(x)，以更新x的值,并且你知道f的导数,然后完成你的工作:导数完全描述了当改变x时，f(x)的发展变化x。如果你想减少f(x)的值,你只需要移动x到方向导数的一个相反方向。

2.4.2张量运算的导数:梯度

梯度是张量运算的导数。它是对多维输入函数的导数概念的推广，也就是说，对以张量为输入的函数的推广。
考虑一个输入向量x，一个矩阵W，一个目标y和一个损失函数loss。您可以使用W计算目标候选人y_pred，并计算目标候选人y_pred与目标y之间的损失或不匹配:

y_pred = dot(W, x)
loss_value = loss(y_pred, y)

如果数据输入x和y被冻结，那么可以将其解释为W到loss值的函数映射值:

loss_value = f(W)

假设W的当前值是W0。那么f在点W0处的导数就是一个张量梯度(f)(W0)，与W形状相同，其中每个系数梯度(f)(W0)[i, j]表示修改W0[i, j]时所观察到的loss_value变化的方向和大小。那个张量梯度(f)(W0)是函数f(W) =loss_value在W0中的梯度。
你之前看到过，函数f(x)对单个系数的导数可以解释为f曲线的斜率，同样，梯度(f)(W0)可以解释为描述f(W)在W0附近的曲率的张量。
出于这个原因,几乎以相同的方式,对于一个函数f(x)，你可以通过在导数的反方向上移动x来减小f(x)的值，对于一个张量的函数f(W)你可以通过在梯度方向上移动W来减小f(W)：例如，W1 = W0 - step * gradient(f)(W0)(其中step是一个很小的比例因子)。这意味着逆着曲率走，直觉上这应该会让曲线更低。注意，需要缩放因子步骤，因为梯度(f)(W0)仅在接近W0时近似于曲率，所以不要离W0太远

2.4.3随机梯度下降法

给定一个可微函数,它在理论上是有可能找到它的最小分析:众所周知,一个函数的最小点的导数为0,所有你要做的就是找到所有导数趋于0的点，并检查哪些点函数值最低。
应用到神经网络中，这意味着分析地寻找权重值的组合，从而得到最小可能的损失函数。这可以通过求解W的方程gradient(f)(W) = 0来实现，这是一个N个变量的多项式方程，其中N是网络中的系数的数量。虽然求解N = 2或N = 3的方程是可能的，但对于真正的神经网络来说，这样做是很棘手的，因为参数的数量永远不少于几千个，而且常常是几千万个。
相反，您可以使用本节开始部分中概述的四步算法:根据随机数据组的当前损失值一点一点地修改参数。因为你在处理一个可微函数，你可以计算它的梯度，这给了你一个有效的方法来实现步骤4。如果你从梯度相反的方向更新权重，每次损失都会小一些:

1. 获取一批训练样本x和相应目标y。
2. 在x上运行网络以获得预测y_pred。
3. 计算批处理上的网络损失，这是y_pred和y之间不匹配的度量。
4. 计算关于网络参数的损失梯度(反向传递backward pass).)。
5. 将参数移动到与梯度相反的方向，例如W -= step * gradient，这样可以减少批处理的损失。
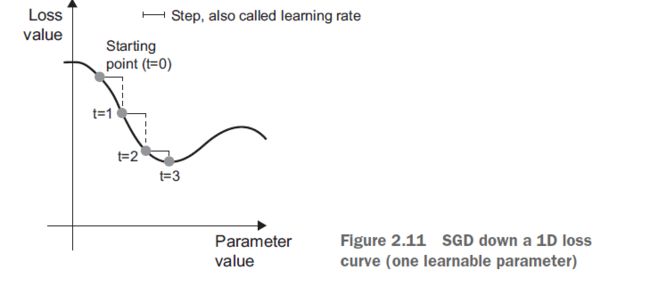
   很容易!我刚才描述的是所谓的小批量随机梯度下降(小批量SGD)。随机这个术语指的是每批数据都是随机抽取的(stochastic是random的科学同义词)。图2.11展示了1D中发生的情况，当网络只有一个参数，而您只有一个训练样本时。

   

   
   正如您所看到的，直观上来说，为step因子选择一个合理的值是很重要的。如果它太小，下降曲线将需要多次迭代，它可能被卡在一个局部极小值。如果step太大，您的更新可能最终会将您带到曲线上完全随机的位置。
   注意，小批量（mini-batch）SGD算法的一个变体是在每次迭代中绘制单个样本和目标，而不是绘制一批数据。这将是真正的SGD(相对于小批量SGD)。另一种极端情况是，可以在所有可用数据上运行每个步骤，称为批处理SGD。每次更新都会更精确，但代价要高得多。这两个极端之间的有效折衷是使用合理尺寸的小批量。
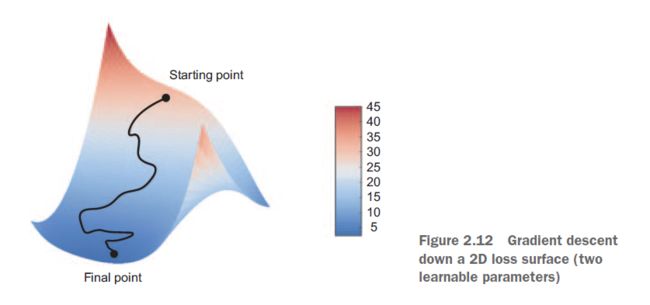
   虽然图2.11展示了一维参数空间中的梯度下降，但实际上您将在高维空间中使用梯度下降:神经网络中的每个权系数都是空间中的自由维数，可能有数万甚至数百万个。为了帮助您建立关于损失表面的直觉，您还可以可视化沿2D损失曲面的梯度下降，如图2.12所示。但是你不可能想象神经网络训练的实际过程是什么样子的——你不能以一种对人类有意义的方式来代表一个100万维的空间。因此，最好记住，你通过这些低维表示发展出来的直觉在实践中可能并不总是准确的。这在历史上一直是深度学习研究领域的一个问题来源。

   

   
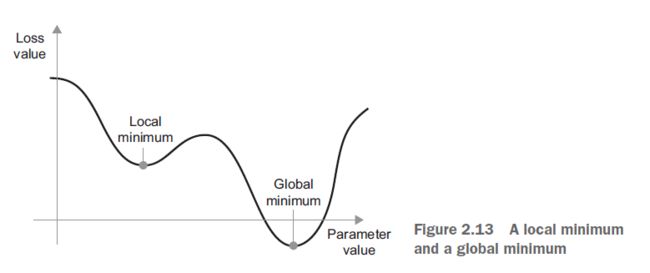
   此外，在计算下一个权重更新时，SGD存在多种变体，这些变体的不同之处在于，考虑到以前的权重更新，而不只是查看梯度的当前值。例如有动量SGD，还有Adagrad, RMSProp和其他几个。这种变体称为优化方法或优化器。特别是动量的概念，它被用在许多这些变体中，值得你注意。动量解决了两个问题：收敛速度和局部极小值。考虑图2.13，它将损耗曲线表示为网络参数的函数。

   

   
   可以看到，在某个参数值附近，存在一个局部极小值:在那个点附近，向左移动会导致损失增加，但向右移动也是如此。
   如果所考虑的参数是通过SGD以较小的学习率进行优化的，那么优化过程就会停留在局部最小值，而不是到达全局最小值。
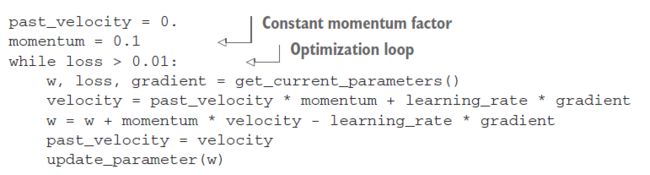
   你可以通过使用动量来避免这些问题，动量从物理学中获得灵感。这里有一个有用的概念，就是把优化过程想象成一个沿着损耗曲线向下滚动的小球。如果它有足够的动量，球就不会卡在峡谷里，最终会达到全球最小。动量是通过在每一步移动球，不仅基于当前斜率值(当前加速度)，而且基于当前速度(由过去的加速度产生)。在实践中，这意味着不仅要根据当前的梯度值，还要根据之前的参数更新来更新参数w，例如在这个简易实现中:

   

   image.png

2.4.4链接导数（Chaining derivatives）:反向传播算法

在前面的算法中，我们随便假设因为一个函数是可微的，我们可以显式地计算它的导数。实际上，神经网络函数由许多张量运算组成，每个张量运算都有一个简单的已知导数。例如，这是一个由三个张量运算(a, b, c)组成的网络f，其权重矩阵为W1, W2和W3:

f(W1, W2, W3) = a(W1, b(W2, c(W3)))

微积分告诉我们这样一个函数链可以用下面的恒等式得到，叫做链式法则:f(g(x)) = f'(g(x)) * g'(x)将链式法则应用于神经网络梯度值的计算，提出了一种算法叫做称为反向传播(Backpropagation有时也称为反向模式微分)。反向传播从最终的损失值开始，从顶层返回到底层，应用链式法则计算每个参数对损失值的贡献。
如今以及未来几年，人们将在现代框架中实现网络，这些框架能够进行符号微分，比如TensorFlow。这意味着，给定一个具有已知导数的操作链，它们可以计算链的梯度函数(通过应用链式法则)，将网络参数值映射到梯度值。当您能够访问这样一个函数时，向后传递被简化为对这个梯度函数的调用。由于有了符号微分，您就不必手工实现反向传播算法。出于这个原因，我们不会浪费您的时间，也不会浪费您的注意力在推导反向传播算法的精确公式上。您所需要的只是对基于梯度的优化如何工作有很好的了解。

2.5 回顾我们的第一个例子

这一章已经结束了，现在你们应该对神经网络的幕后工作有了一个大致的了解。让我们回到第一个示例，根据前面三部分中所学到的内容回顾每一部分。
首先是输入数据

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

现在你知道了输入的图像存储在Numpy张量中，这些张量在这里分别格式化为形状为float32张量(60000,784)(训练数据)和(10000，784）(测试数据)。
这是我们的网络：

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))

在你明白了这个网络是由两个稠密层组成的链，每个层对输入数据应用一些简单的张量运算，这些运算涉及到权重张量。权重张量是各层的属性，是网络知识持续存在的地方。
这是网络编译的步骤:

network.compile(optimizer='rmsprop',
                  loss='categorical_crossentropy',
                  metrics=['accuracy'])

在你明白了categorical_crossentropy是一个损失函数，它被用作一个反馈信号用来学习权重张量，这是训练阶段的目标。你也知道这种损失的减少是通过小批量随机梯度下降来实现的。作为第一个参数传递的rmsprop优化器定义了控制梯度下降特定使用的确切规则。
最后是训练循环:

network.fit(train_images, train_labels, epochs=5, batch_size=128)

现在您了解了调用fit时会发生什么:网络将开始以128个样例的小批量迭代训练数据，重复5次(对所有训练数据的每次迭代称为epoch)。在每次迭代中，网络会计算出与批处理损失相关的权重梯度，并更新权重。
在这5个迭代之后，该网络将进行2,345次梯度更新(每轮迭代469次)，网络的损失将会足够低，因此该网络将能够对手写数字进行高精度的分类。
至此，你已经知道了关于神经网络的大部分知识。

章节总结

• 学习（learning）意味着找到一组模型参数的组合，使给定的一组训练数据样本及其相应目标的损失函数最小化。
• 学习是通过绘制随机批量的数据样本及其目标，并计算网络参数相对于批量损失的梯度来实现的。然后，将网络参数在与梯度相反的方向上移动一点(移动幅度由学习率定义)。
• 由于神经网络是可微张量运算的链，因此可以应用导数的链式法则来找到将当前参数和当前数据批映射到梯度值的梯度函数，从而使整个学习过程成为可能。
• 您将在以后的章节中经常看到的两个关键概念是loss和optimizers。在开始向网络提供数据之前，您需要定义两件事。
• 损失是你在训练过程中试图最小化的数量，所以它应该代表你想要解决的任务的成功程度。
• 优化器指定了用于更新参数的精确方法:例如，它可以是RMSProp优化器，带动量的SGD等等

额外阅读

梯度数学知识点：http://netedu.xauat.edu.cn/jpkc/netedu/jpkc/gdsx/homepage/5jxsd/51/513/5308/530807.htm

 

作者：凤凰花开那一天
链接：https://www.jianshu.com/p/ba51e470b736
来源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。