upc 2019年我能变强组队训练赛第三场 F A Rational Sequence G Growing Rectangular Spiral H Farey Sums 思维训练题。
先感慨一下,思维规律场也没打出自己的优势来,哎。。。有些题还是没敢想没敢写。还是不难解决的。
A Rational Sequence
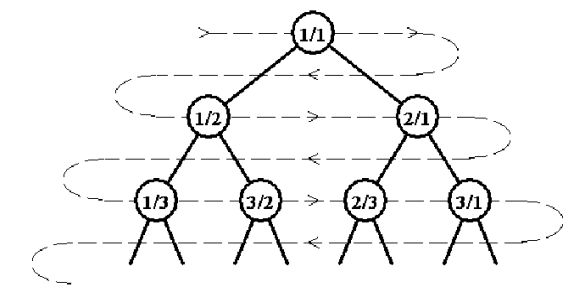
An infinite full binary tree labeled by positive rational numbers is defi ned by:
• The label of the root is 1/1.
• The left child of label p/q is p/(p+q).
• The right child ofl abel p/q is (p+q)/q.
The top of the tree is shown in the following figure:
A rational sequence is defined by doing a level order (breadth first) traversal of the tree (indicated by the light dashed line). So that:
F(1) = 1/1, F(2) = 1/2, F(3) = 2/1, F(4) = 1/3, F(5) = 3/2, F(6) = 2/3, . . .
Write a program which takes as input a rational number, p/q, in lowest terms and fi nds the next rational number in the sequence. That is, if F(n) = p/q, then the result is F(n + 1).
输入
The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets that follow. Each data set should be processed identically and independently.
Each data set consists of a single line of input. It contains the data set number, K, which is then followed by a space, then the numerator of the fraction, p, followed immediately by a fonward slash (/),followed immediately by the denominator of the fraction, q. Both p and q will be relatively prime and 0 ≤ p, q ≤ 2147483647.
输出
For each data set there is a single line of output. It contains the data set number, K, followed by a single space which is then followed by the numerator of the fraction, followed immediately by a forward slash (‘/’) followed immediately by the denominator of the fraction. Inputs will be chosen such that neither the numerator nor the denominator will overfl ow a 32-bit integer.
样例输入
复制样例数据
5
1 1/1
2 1/3
3 5/2
4 2178309/1346269
5 1/10000000
样例输出
1 1/2
2 3/2
3 2/5
4 1346269/1860498
5 10000000/9999999题意:给定一个二叉树序列,p/q,左孩子=p/(p+q) 又孩子=(p+q)/p;随便给你一个pq 求下一项的pq值。
思路:就是一个思维题啊,不需要什么dfs往上走到公共节点再走下来判断,直接用式子往上推就可以了,推到父节点等高的一条链上,然后可根据左子树的值确定又数的数。因为一条线上的p都相等。
#include
#define ll long long
using namespace std;
#pragma GCC optimize(2)
int main()
{
ll t,m,n,i,j,k,sum,p;
scanf("%lld",&t);
for(p=1;p<=t;p++)
{
scanf("%d",&sum);
ll x,y;
scanf("%lld/%ldl",&x,&y);
printf("%lld ",p);
if(x==1&&y==1)
{
printf("1/2\n");
}
else if(x==1)
{
printf("%lld/%lld\n",y,y-x);
}
else if(y==1)
{
printf("1/%lld\n",x+1);
}
else
{
ll ans=0;
while(x>y)
{
x=x-y;
ans++;
}
printf("%lld/%lld\n",y,ans*y+y-x);
}
}
return 0;
}
Farey Sums
Given a positive integer, N, the sequence of all fractions a/b with (0 < a ≤ b), (1 < b ≤ N) and a and b relatively prime, listed in increasing order, is called the Farey Sequence of order N.
For example, the Farey Sequence of order 6 is:
0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1/1
If the denominators of the Farey Sequence of order N are:
b[1], b[2], . . . , b[K]
then the Farey Sum of order N is the sum of b[i]/b[i + 1] from i = 1 to K—1.
For example, the Farey Sum of order 6 is:
1/6 + 6/5 + 5/4 + 4/3 + 3/5 + 5/2 + 2/5 + 5/3 + 3/4 + 4/5 + 5/6 + 6/1 = 35/2
Write a program to compute the Farey Sum of order N (input).
输入
The first line of input contains a single integer P, (1 ≤ P ≤ 10000), which is the number of data sets that follow. Each data set should be processed identically and independently.
Each data set consists of a single line of input. It contains the data set number, K, followed by the order N, (2 ≤ N ≤ 10000), of the Farey Sum that is to be computed.
输出
For each data set there is a single line of output. The single output line consists of the data set number,K, followed by a single space followed by the Farey Sum as a decimal fraction in lowest terms. If the denominator is 1, print only the numerator.
样例输入
复制样例数据
4
1 6
2 15
3 57
4 9999
样例输出
1 35/2
2 215/2
3 2999/2
4 91180457/2题意:定义一个 Farey 序列,然后求 b[i]/b[i + 1] 的和;
先打表找规律可求得前20项每一项的差值都为3的倍数;而且差的倍数正好是oula【i】
可以简单的证一下:原来的a/b+b/a变成了a/(a+b)+(a+b)/b+b/(a+b)+(a+b)/a=a/b+b/a+3 也就是多了一个三。然后找他有几个就可以了,打表找出前面分母观察规律就可以了。
#include
#define ll long long
using namespace std;
const int maxx=1e4+1000;
int sushu[maxx];
bool biaoji[maxx];
ll i,j,m,n,k;
int cnt=0;
ll ola[maxx];
ll a[maxx];
void olashai()
{
memset(biaoji,true,sizeof(biaoji));
for(i=2;i
Growing Rectangular Spiral
A growing rectangular spiral is a connected sequence of straightline segments starting at the origin. The fi rst segment goes right (positive x direction). The next segment goes up (positive y direction). The next segment goes left (negative x direction). The next segment goes down (negative y direction) and the sequence of directions repeats. Each segment has integer length and each segment is at least one unit longer than the previous segment. In the spiral on the right, the segment lengths are 1, 2, 4, 6, 7, 9,11, 12, 15, 20.
Write a program to determine the shortest growing rectangular spiral (in total length) that ends at a given integer point (x, y) in the fi rst quadrant or determine that there is no such spiral.
输入
The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets that follow. Each data set should be processed identically and independently.
Each data set consists of a single line of input consisting of three space separated decimal integers.
The first integer is the data set number. The next two integers are the x and y coordinates of the desired end point (1 ≤ x ≤ 10000, 1 ≤ y ≤ 10000).
输出
For each data set there is a single line of output. If there is no spiral solution, the line consists of the data set number, a single space and ‘NO PATH’ (without the quotes). If there is a solution, the line consists of the data set number, a single space, the number of segments in the solution, a single space,followed by the lengths of the segments in order, separated by single spaces. The input data will be chosen so that no path requires more than 22 segments.
样例输入
复制样例数据
3
1 1 1
2 3 5
3 8 4
样例输出
1 NO PATH
2 2 3 5
3 6 1 2 3 9 10 11
题意:走一个逆时针的螺旋线,切走的步数必须严格递增,问最少步数走到(x,y)点,如果不能则输出NO PATH ,也是个思维题啊:
观察一下就可得出规律了,如果x
其他情况走六步就可以,然后按最少的递增序列走y的坐标正好=4,所以当y大于4时无解。然后就是解方程了,b=x+2显而易见,然后设c=b+1可得出a=5+x-y,上面图写错了。。。算了懒得改了。
#include
#define ll long long
using namespace std;
const int maxx=1e4+1000;
int main()
{
int t;
scanf("%d",&t);
int sum,x;
for(int p=1;p<=t;p++)
{
int y;
scanf("%d%d%d",&sum,&x,&y);
if(y==x)
{
printf("%d NO PATH\n",p);
}
else if(x
其他情况走六步就可以,然后按最少的递增序列走y的坐标正好=4,所以当y大于4时无解。然后就是解方程了,b=x+2显而易见,然后设c=b+1可得出a=5+x-y,上面图写错了。。。算了懒得改了。
#include
#define ll long long
using namespace std;
const int maxx=1e4+1000;
int main()
{
int t;
scanf("%d",&t);
int sum,x;
for(int p=1;p<=t;p++)
{
int y;
scanf("%d%d%d",&sum,&x,&y);
if(y==x)
{
printf("%d NO PATH\n",p);
}
else if(x