[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记
本文仅为个人的学习笔记,对论文或者网上的资料作总结以及加入个人的理解,对论文或者在线资料可能有诸多理解不准确的地方 ,见谅。
主要参考资料:
如何理解 Graph Convolutional Network(GCN)? - superbrother的回答 - 知乎 https://www.zhihu.com/question/54504471/answer/332657604
Chebyshev多项式作为GCN卷积核 - superbrother的文章 - 知乎 https://zhuanlan.zhihu.com/p/106687580
图卷积网络 GCN Graph Convolutional Network(谱域GCN)的理解和详细推导-持续更新https://blog.csdn.net/yyl424525/article/details/100058264
Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//Advances in neural information processing systems. 2016: 3844-3852.
1.为什么要有GCN?
一开始看论文非常疑惑,有CNN为什么还需要有GCN。
(1)首先,CNN在图片等数据上好用,是因为我们很容易找到他们的邻接点。这些邻接点其实就是这个核的receptive fields(感受野)。
在图片中,CNN是通过卷积核来提取图片的局部特征。卷积是通过对当前像素点以及其临近的像素点进行加权求和。
类似图片这种数据是欧几里得结构数据 Euclidean Structure Data ,他们排列整齐,我们很容易找到他们临近的点。
(2)在graph即拓扑图中,找到邻接点可就不那么简单了。
对于graph,就是拓扑图,例如下图,我们该怎么样去找他们临近的点就成了问题。这种拓扑图是 非欧几里德结构数据 Non-Euclidean Structure Data,较难定义他们的邻居结点,或者每个节点的邻居结点不同,那我们就不能用同一个尺寸的卷积核对整个拓扑图进行学习了。
(3)因此研究GCN的动机:
1.因为拓扑图中每个顶点的邻接点数目不同,无法用同一卷积核完成卷积。
2.像User data on social networks, gene data on biological regulatory networks, log data on telecommunication networks, or text documents on word embeddings 这种可以用拓扑图建模的数据又非常值得研究。
因此我们需要找出一个适合在拓扑图上,应用CNN的方法。
2.CNN应用于graph上的两类方法
2.1在空间上
文章《Learning Convolutional Neural Networks for Graphs》定义了如何寻找拓扑图中某个顶点的邻居顶点来确定核的感受野。
(文章还没太看懂,之后还要再看一下)流程上是,先对一个拓扑图的顶点进行打标签(重点在于如何打标签,就是需要找到一个序列,对于该拓扑图来说,每个顶点所在的序列号反映了这些顶点所在的空间相对位置),打完标签之后对这个拓扑图的序列选出前一些顶点,然后找这些顶点的邻居结点...
2.2 在频域上
使用图信号处理(graph signal processing),因为定义了图上的傅里叶变换,然后也延伸出了图上的卷积。论文Convolutional neural networks on graphs with fast localized spectral filtering 采用的就是频域上的方法。
文中给出的解释是:在空间的角度上,拓扑图的卷积的平移不变性没有一个很好的数学定义。
3.一些数学知识
3.1拉普拉斯矩阵
拉普拉斯矩阵的定义:
拉普拉斯矩阵是图论中用到的一种重要矩阵,给定一个有n个顶点的图 G=(V,E),其拉普拉斯矩阵被定义为 L = D-A,D其中为图的度矩阵,A为图的邻接矩阵。把W的每一列元素加起来得到N个数,然后把它们放在对角线上(其它地方都是零),组成一个N×N的对角矩阵,记为度矩阵D。其实度矩阵(对角线元素)表示的就是原图中每个点的度数,即由该点发出的边之数量。
拉普拉斯矩阵有下面的三个性质:
(因为他是一个半正定的对称矩阵)
此处特征向量可以转化成正交矩阵,即特征向量的逆即为特征向量的转置。如下图所示:
拉普拉斯矩阵的分解
根据论文可知,拉普拉斯可以进行特征值分解,用于分解的基是拉普拉斯矩阵的特征向量,也叫图傅里叶的基(可以类比与信号与系统中教的一维傅里叶变换的模式e^(-jwt)),而特征值就是理解为该图的频率的大小(即该图在该特征向量上的分量的大小)。
3.2傅里叶变换的性质应用
论文中:
实际上用到了性质:A与B的卷积=傅里叶逆变换(傅里叶变换(A)*傅里叶变换(B))。因为这里是矩阵形式,所以用到了哈达玛积。结合文章中给的傅里叶变换以及其逆变换的表示形式:![]() 就可以理解了。
就可以理解了。
3.3GCN的卷积核
3.3.1普通卷积核
论文到了这部分有点难以理解,数学知识有些不足了,所以先将此部分的资料拷贝于此处,也将目前的理解写与此处(可能是写成矩阵形式不习惯)
输入与卷积核的卷积可以根据以下定理进行计算:
这里就是利用了上述的性质,卷积核与输入的卷积=傅里叶逆变换(傅里叶变换(输入)*傅里叶变换(卷积核))。然后下面将卷积核的傅里叶变换写成对角矩阵的形式。
自己的理解就是,这种卷积核,我们需要训练的就是n个h(i)的参数。
然后,论文中说,这种卷积核的缺点有两个:(1)首先这种卷积核提取的不是局部特征?(2)因为要获取n个参数,所以时间复杂度是O(n)?(这里是怎么推导训练时间复杂度的?) 为了解决这个问题,论文提出使用多项式参数化的滤波器。
3.3.2切比雪夫多项式参数化的滤波器
使用卷积核![]() 进行卷积
进行卷积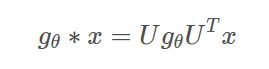 有一个缺点就是计算的复杂度大:因为需要就进行图傅里叶基的乘法:
有一个缺点就是计算的复杂度大:因为需要就进行图傅里叶基的乘法:![]()
文章使用了切比雪夫多项式对卷积核进行近似,近似之后,我们就可以不用进行特征分解(可以把U代进去Tk(^)里面变成Tk(L),各阶数据也能利用契比雪夫多项式的性质递推算出),如下图:
那么,与卷积核的卷积操作就变成了下图:
这里的K-localized是因为这个定理:即拉普拉斯矩阵的s次方中,若m,n不为0,那么说明mn之间至少存在一条通路(这条通路的跳数是小于等于s的)。那么我理解的是:K-localized就是意味着,如果L^k次方在某个顶点不为0,那么说明这个顶点是有小于等于距离他k跳的邻居。而对于规定的K,由于L^K对顶点大于它K跳的邻居时为0,因此该邻居在加权时不会被加权进来的(因为此时L^K=0)。
4.卷积层的传播规则
此处似乎一般上会把K定义为1,即使用切比雪夫1阶多项式进行近似,每一层提取的都是该顶点及距离其跳数为1的顶点的特征。如果要扩大感受野,则进行多层的级联,如下图:
如果A中不加上单位阵,则在传播中顶点自身的特征信息就没有了。
但对于论文中的这个输出以及训练的方式还是没有太好的理解到:
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第1张图片](http://img.e-com-net.com/image/info8/8fd087f9f03b431989159c1d918c03e2.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第2张图片](http://img.e-com-net.com/image/info8/e7a2b1ecc7944e4ea854cf7c63494598.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第3张图片](http://img.e-com-net.com/image/info8/af834043fa44484b985a2ad595822bbf.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第4张图片](http://img.e-com-net.com/image/info8/fd12230c820c4706b35e9e835e107440.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第5张图片](http://img.e-com-net.com/image/info8/61905c67d2764d43b265a5ac117baf63.png)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第6张图片](http://img.e-com-net.com/image/info8/4643ff27fc004da085f71a424d01169d.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第7张图片](http://img.e-com-net.com/image/info8/d6527ce58b6f4205ae1058ab8cfed46e.jpg)

![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第8张图片](http://img.e-com-net.com/image/info8/9d397dcaa2764ae38ed181b81f97cdf0.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第9张图片](http://img.e-com-net.com/image/info8/62717a9b419d43ec9ee6ae939bfe83b2.jpg)

![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第10张图片](http://img.e-com-net.com/image/info8/942a707ee23044eba55cb1fbfdc3dbd3.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第11张图片](http://img.e-com-net.com/image/info8/652e946f60f542e2abcbb0b0b273ee86.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第12张图片](http://img.e-com-net.com/image/info8/fed426ce6c2b466b8251054b36f3188b.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第13张图片](http://img.e-com-net.com/image/info8/6ef5a455128f4f83ab5fcf206bda783f.jpg)
![[深度学习笔记][CNN/GCN]Graph Convolutional Network学习笔记_第14张图片](http://img.e-com-net.com/image/info8/69de34f2427743fabf70dee5ec712995.jpg)