【C语言基础】->自幂数优化->这个算法快得像一道闪电
自幂数
-
- Ⅰ 自幂数的定义
- Ⅱ 需求分析
- Ⅲ 算法优化
-
- a. 得到当前数字的位数
- b. 判断自幂数
- Ⅳ 完整代码
Ⅰ 自幂数的定义
自幂数是指一个 n 位数,它的每个位上的数字的 n 次幂之和等于它本身。(例如:当n为3时,有1^3 + 5^3 + 3^3 = 153,153即是n为3时的一个自幂数)
自幂数包括:独身数、水仙花数、四叶玫瑰数、五角星数、六合数、北斗七星数、八仙数、九九重阳数、十全十美数
n为1时,自幂数称为独身数。显然,0,1,2,3,4,5,6,7,8,9都是自幂数。
n为2时,没有自幂数。
n为3时,自幂数称为水仙花数,有4个:153,370,371,407;
n为4时,自幂数称为四叶玫瑰数,共有3个:1634,8208,9474;
n为5时,自幂数称为五角星数,共有3个:54748,92727,93084;
n为6时,自幂数称为六合数, 只有1个:548834;
n为7时,自幂数称为北斗七星数, 共有4个:1741725,4210818,9800817,9926315;
n为8时,自幂数称为八仙数, 共有3个:24678050,24678051,88593477;
n为9时,自幂数称为九九重阳数,共有4个:146511208,472335975,534494836,912985153;
n为10时,自幂数称为十全十美数,只有1个:4679307774。
Ⅱ 需求分析
该程序的目的是输出一定范围内的所有自幂数,要判断一个数是不是自幂数,我们需要得到它的位数,然后根据每位的位数次方之和来判断该数是不是自幂数。
得到位数以及次方和,便是这个程序的主要步骤,因此,优化该程序也应从这两部的效率最高的方法考虑。
在我的哥德巴赫猜想验证的博客中,我给出了一个代码从最初级到极限的算法优化全部步骤,感兴趣的同学可以移步去看那篇文章,在此我不再赘述,直接考虑自幂数算法的极限情况。
【C语言】->哥德巴赫猜想验证->筛选法->算法极限优化之你不可能比我快
Ⅲ 算法优化
a. 得到当前数字的位数
关于这一步,惯常的想法是通过不断 /10 得到位数,事实上最快的做法是用 if 条件语句直接判断。由于int类型最大数是42亿左右,十全十美数已经超过了这个范围,所以我们只考虑十位以下的数。
int getBits(int number) {
if (number >= 100000000 && number < 1000000000) {
return 9;
}
if (number >= 10000000 && number < 100000000) {
return 8;
}
if (number >= 1000000 && number < 10000000) {
return 7;
}
if (number >= 100000 && number < 1000000) {
return 6;
}
if (number >= 10000 && number < 100000) {
return 5;
}
if (number >= 1000 && number < 10000) {
return 4;
}
if (number >= 100 && number < 1000) {
return 3;
}
if (number >= 10 && number < 100) {
return 2;
}
if (number >= 0 && number < 10) {
return 1;
}
}
这里还有个需要注意的地方,就是要从最大位数开始判断,因为往后数字越大最后判断自幂数的时间就越长,所以把最大的数放在靠上面的语句,这样可以更快的得到更大数的位数,即使只是省了几行语句的时间。
b. 判断自幂数
要知道一个数是不是自幂数,我们需要将每一位的数字的位数次方加起来,然后和本身做比较。这就牵扯到每次判断可能都要调用pow()函数,但是这样是很花时间的。
在做哥德巴赫猜想验证时,我们先生成了一个质数池,每次判断一个数是不是质数,直接在质数池中取就知道了。同样的思路,我们判断自幂数时,不用当场算它的幂级数,而是直接取。这就用到了二维数组。
因为每个数字的每一位上只可能是0 到 9 这十个数字,且数字的位数也是0 到 9位,所以其幂指数也是只可能是 0 到 9 这十个数字。所以我们先算完,然后存入二维数组中,到时候直接调取就好了。
const int array[10][10] = {
/*0*/ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
/*1*/ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
/*2*/ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81,
/*3*/ 0, 1, 8, 27, 16*4, 125, 36*6, 49*7, 64*8, 81*9,
/*4*/ 0, 1, 16, 81, 16*4*4, 125*5, 36*6*6, 49*7*7, 64*8*8, 81*9*9,
/*5*/ 0, 1, 32, 243, 16*4*4*4, 125*5*5, 36*6*6*6, 49*7*7*7, 64*8*8*8, 81*9*9*9,
/*6*/ 0, 1, 64, 729, 16*4*4*4*4, 125*5*5*5, 36*6*6*6*6, 49*7*7*7*7, 64*8*8*8*8, 81*9*9*9*9,
/*7*/ 0, 1, 128, 729*3, 16*4*4*4*4*4, 125*5*5*5*5, 36*6*6*6*6*6, 49*7*7*7*7*7, 64*8*8*8*8*8, 81*9*9*9*9*9,
/*8*/ 0, 1, 256, 729*3*3, 16*4*4*4*4*4*4, 125*5*5*5*5*5, 36*6*6*6*6*6*6, 49*7*7*7*7*7*7, 64*8*8*8*8*8*8, 81*9*9*9*9*9*9,
/*9*/ 0, 1, 512, 729*3*3*3, 16*4*4*4*4*4*4*4, 125*5*5*5*5*5*5, 36*6*6*6*6*6*6*6, 49*7*7*7*7*7*7*7, 64*8*8*8*8*8*8*8, 81*9*9*9*9*9*9*9,
};
我用const定义了一个二维数组,所以不需要每一个值我都计算出来,这些数会在预编译的过程中由C语言编译器直接计算完成,不会占用程序运行的时间。
其行为幂指数,列为对应的位。
所以判断自幂数的代码如下
boolean isSelfPower(int number, int bits) {
int i;
int bit;
int sum = 0;
int num = number;
for (; sum <= number && num; num /= 10) {
bit = num % 10;
sum += power(bits, bit);
}
return sum == number;
}
int power(int bits, int number) {
return array[bits][number];
}
那么这两个关键步骤已经优化完成了。
Ⅳ 完整代码
#include 到了最大位,n为9时
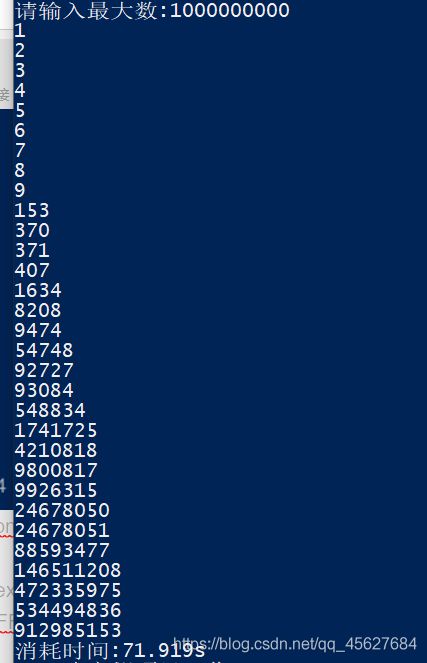
消耗了一分多,前面其实都很快,找到最后一个数花费了很多时间。
所以快的像一道闪电是骗你们的,不过已经很快了,毕竟不是个简单的事。
下面这个才是快得像闪电一样,并且已经优化到了极致。感兴趣的同学可以移步此处。
【C语言】->哥德巴赫猜想验证->筛选法->算法极限优化之你不可能比我快
以上即为我对查找自幂数的算法优化,大家可以再多加尝试,找到更好的方法来优化。