【数据结构与算法】->算法->排序(一)->冒泡排序&插入排序&选择排序
排序(一)
-
- Ⅰ 前言
- Ⅱ 如何分析一个“排序算法”
-
- A. 排序算法的执行效率
-
- 1.最好情况、最坏情况、平均情况时间复杂度
- 2.时间复杂度的系数、常数、低阶
- 3.比较次数和交换(或移动)次数
- B. 排序算法的内存消耗
- C. 排序算法的稳定性
- Ⅲ 冒泡排序(Bubble Sort)
-
- 1. 详解
- 2. 冒泡排序内存消耗
- 3. 冒泡排序稳定性
- 4. 冒泡排序时间复杂度
-
- ① 有序度
- ② 逆序度
- 5. 拓展-直接交换排序
- Ⅳ 插入排序(Insertion Sort)
-
- 1. 详解
- 2. 插入排序内存消耗
- 3. 插入排序稳定性
- 4. 插入排序时间复杂度
- 5. 拓展-希尔排序(Shell Sort)
-
- ① 详解
- ② 希尔排序内存消耗
- ③ 希尔排序稳定性
- ④ 希尔排序时间复杂度
- Ⅴ 选择排序(Selection Sort)
-
- 1. 详解
- 2.选择排序内存消耗
- 3.选择排序稳定性
- 4.选择排序时间复杂度
- Ⅵ 为什么插入排序比冒泡排序更受欢迎?
Ⅰ 前言
排序对于任何一个程序员来说,都不会陌生。一般新手学的第一个算法,就是排序,而且大都是冒泡排序。大部分编程语言中,也提供了排序函数。排序在算法中是非常重要的,我将会用三篇文章,讲清楚经典的几个排序算法。
排序算法太多了,很多可能你连名字都没听说过,比如猴子排序、睡眠排序、面条排序等等,这三篇文章着重讲最经典和最常用的几个:冒泡排序、插入排序、选择排序、归并排序、快速排序、基数排序、计数排序、桶排序。我按照时间复杂度把它们分成了三类,对应三篇文章。
| 排序算法 | 时间复杂度 | 是否基于比较 |
|---|---|---|
| 冒泡、插入、选择 | O(n2) | 是 |
| 快排、归并 | O(nlog2n) | 是 |
| 桶、计数、基数 | O(n) | 否 |
Ⅱ 如何分析一个“排序算法”
学习排序算法,我们除了要学习它的算法原理、代码实现之外,更重要的是要学会如何评价、分析一个排序算法。那么,分析一个排序算法要从哪几个方面入手呢?
A. 排序算法的执行效率
对于排序算法执行效率的分析,我们一般会从以下几个方面来衡量:
1.最好情况、最坏情况、平均情况时间复杂度
我们在分析排序算法的时间复杂度时,要分别给出最好情况、最坏情况、平均情况下的时间复杂度。除此之外,你还要说出最好、最坏的时间复杂度对应的要排序的原始数据是什么样的。
如果对时间空间复杂度的计算有迷惑,可以看我下面这篇文章
【数据结构与算法】->详解时间复杂度和空间复杂度
2.时间复杂度的系数、常数、低阶
我们知道,时间复杂度反应的是数据规模 n 很大的时候的一个增长趋势,所以它表示的时候会忽略系数、常数、低阶。但是实际的软件开发中,我们排序的可能是 10 个、 100 个、 1000 个这样规模很小的数据,所以,在对同一阶时间复杂度的排序算法性能对比的时候,我们就要把系数、常数、低阶也考虑进来。
3.比较次数和交换(或移动)次数
前两篇文章中,我讲解的都是基于比较的排序算法。基于比较的排序算法的执行过程,会涉及到两种操作,一种是元素比较大小,另一种是元素交换或移动。所以,如果我们在分析排序算法的执行效率的时候,应该把比较次数和交换(或移动)次数也考虑进去。
B. 排序算法的内存消耗
算法的内存消耗可以通过空间复杂度来衡量,排序算法也不列外。不过,针对排序算法的空间复杂度,我们还引入了一个新的概念,原地排序(Sorted in place)。原地排序算法,就是特指空间复杂度是 O(1) 的排序算法,这篇文章中要讲的四个算法都是原地排序算法。
C. 排序算法的稳定性
针对排序算法,我们还有一个重要的度量指标,稳定性。这个概念是说,如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
比如一组数据 1, 13, 2, 7, 0, 4, 7,按照大小排序之后就是 0, 1, 2, 4, 7, 7, 13。
这组数据里有两个 7。经过某种排序算法排序后,如果两个 7 的前后顺序没有变,那我们就把这种排序算法叫作稳定的排序算法,如果前后的顺序发生变化,那对应的排序算法就叫作不稳定的排序算法。
这个的意义在哪里呢,既然都是 7 。实际上,在练习的时候我们排序都用的是数字,但是真正应用上,我们要排的可能就是一组对应,根据其键值来排,那么稳定性就很重要了。
比如说,我们现在要给电商交易系统中的“订单”排序。订单有两个属性,一个是下单时间,一个是订单金额。如果我们现在有十万条订单数据,我们希望按照金额从小到大对订单数据进行排序,对于金额相同的订单,我们希望按照下单时间从早到晚排序。对于这样一个需求我们应该怎么做呢?
很容易想到的一个方法是:先按照金额对订单数据进行排序,然后,再遍历排序之后的订单数据,对于每个金额相同的小区间再按照下单时间排序。这种排序思路很容易理解,但是实现起来会很麻烦。
借助稳定排序算法,这个问题可以非常简洁地解决。思路是这样的:我们先按照下单时间给订单排序,排序完成之后,我们用稳定排序算法,按照订单金额重新排序。两遍排序之后,我们得到的订单数据就是按照金额从小到大排序,金额相同的订单按照下单时间从早到晚排序的。
对排序算法的分析有个大概认识之后,我们来看具体的算法。
Ⅲ 冒泡排序(Bubble Sort)
1. 详解
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。
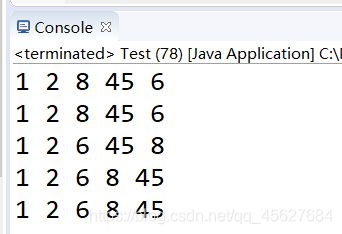
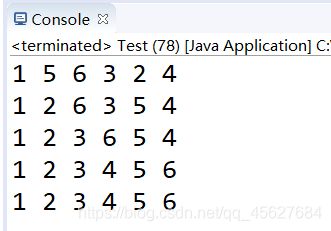
我用一组数据来展示一遍冒泡排序的整个过程。比如我们要排序 {2, 1, 8, 45, 6}
第一次冒泡:
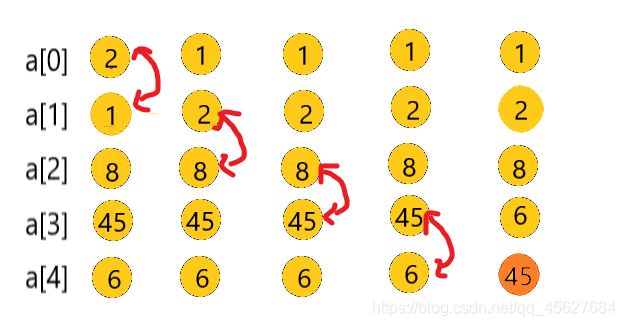
可以看出,经过一次冒泡操作后, 45 这个元素已经存储在正确的位置上。要想完成所有数据的排序,我们只要进行 5 次这样的冒泡操作就可以了。

实际上,这个冒泡的过程还可以优化。当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再继续执行后续的冒泡操作了。
我用Java简单实现一下这个算法。
package com.tyz.about_sort.core;
public class BubbleSort {
public BubbleSort() {
}
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
boolean isChanged = false; //判断此轮是否有数据交换
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
isChanged = true;
}
}
if (!isChanged) {
break;
}
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k] + " ");
}
System.out.println();
}
}
}
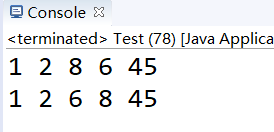
测试代码如下,我还是用做例子的一组数据
package com.tyz.about_sort.test;
import com.tyz.about_sort.core.BubbleSort;
public class Test {
public static void main(String[] args) {
int[] arr = {
2, 1, 8, 45, 6};
BubbleSort.bubbleSort(arr);
}
}
结果如下,只用了两轮就结束了
现在,结合之前的分析,我们逐一来看。
2. 冒泡排序内存消耗
冒泡的过程只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为 O(1) ,是一个原地排序算法。
3. 冒泡排序稳定性
在冒泡排序中,只有交换才可以改变两个元素的前后顺序,为了保证冒泡排序的稳定性,当有相邻的两个元素大小相等时,我们不做交换,相同大小的数据在排序前后不会改变顺序,所以冒泡排序是稳定的排序算法。
4. 冒泡排序时间复杂度
最好情况下,要排序的数据已经是有序的了,我们只需要进行一次冒泡操作,就可以结束了,所以最好情况时间复杂度是 O(n) 。而最坏的情况是,要排序的数据刚好是倒序排列的,我们需要进行 n 次冒泡操作,所以最坏情况时间复杂度为 O(n2) 。
最好、最坏情况下的时间复杂度很容易分析,那平均情况下的时间复杂度是多少呢?在我的第一篇文章里介绍过,平均时间复杂度就是加权平均期望时间复杂度,分析的时候要结合概率论的知识。
对于包含 n 个数据的数组,这 n 个数据就有 n! 种排列方式。不同的排列方式,冒泡排序执行的时间肯定是不同的。如果用概率论方法定量分析平均时间复杂度,涉及的数学推理和计算就会很复杂。所以在这里我给出另一个思路,通过 有序度 和 逆序度 这两个概念来进行分析。
① 有序度
有序度是数组中具有有序关系的元素对的个数。有序元素对用数学表达式表示就是这样:
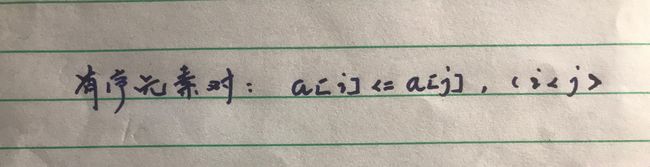

同理,对于一个倒序排列的数组,比如 6, 5, 4, 3, 2, 1,有序度就是 0;对于一个完全有序的数组,比如 1, 2, 3, 4, 5, 6,有序度就是 n * (n - 1) / 2,也就是15。我们把这种完全有序的数组的有序度叫作 满有序度。
② 逆序度
逆序度的定义正好跟有序度相反,(默认从小到大为有序)。
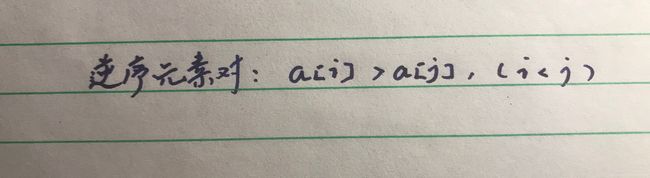
关于这三个概念,我们还可以得到一个公式:逆序度 = 满有序度 - 有序度
我们排序的过程就是一种增加有序度,减少逆序度的过程,最后达到满有序度,就说明排序完成了。
冒泡排序包含两个操作原子,比较 和 交换。每交换一次,有序度就加 1.不管算法怎么改进,交换次数总是确定的,即为 逆序度,也就是 n * (n - 1) / 2 - 初始有序度。
对于包含 n 个数据的数组进行冒泡排序,平均交换次数是多少呢?最坏情况下,初始状态的有序度为 0,所以要进行 n * (n - 1) / 2 次交换。最好情况下,初始状态的有序度是 n * (n - 1) / 2,就不需要交换。我们可以取个中间值 n * (n - 1) / 4,来表示初始有序度既不是很高也不是很低的平均情况。
换句话说,平均情况下,需要 n * (n - 1) / 4 次交换操作,比较操作肯定要比交换操作多,而复杂度的上限是 O(n2),所以平均情况下的时间复杂度就是 O(n2)。
这个平均时间复杂度推导过程其实并不严格,但是很多时候很实用,毕竟概率论的定量分析太复杂,不太好用。
5. 拓展-直接交换排序
这里再补充一个直接交换排序,这个算法和冒泡排序是很像的,思路也大致相同。差别就是冒泡排序是相邻两个数据的比较,而直接交换排序是一个数据不断和后面的数据比较,直到其位置合适。
我直接附上代码,大家可以看看,这个是比较简单的。
public static void directExchangeSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
for (int j = i + 1; j < arr.length; j++) {
if (arr[i] > arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k] + " ");
}
System.out.println();
}
}
测试代码如下
package com.tyz.about_sort.test;
//import com.tyz.about_sort.core.BubbleSort;
import com.tyz.about_sort.core.DirectExchangeSort;
public class Test {
public static void main(String[] args) {
int[] arr = {
2, 1, 8, 45, 6};
// BubbleSort.bubbleSort(arr);
DirectExchangeSort.directExchangeSort(arr);
}
}
Ⅳ 插入排序(Insertion Sort)
1. 详解
我们先思考一个问题,一个有序的数组,我们往里面添加一个新的数据后,如何继续保持数据有序呢?很简单,我们只要遍历数组,找到数据应该插入的位置将其插入即可。
这是一个动态排序的过程,即动态地往有序集合中添加数据,我们可以通过这种方法保持集合中的数据一直有序。而对于一组静态数据,我们也可以借鉴上面讲的插入方法,来进行排序,于是就有了插入排序算法。
首先,我们将数组中的数据分为两个区间,已排序区间 和 未排序区间。初始已排序区间只有一个元素,就是数组中的第一个元素。插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
插入排序也包含两种操作,一种是元素的比较,一种是元素的移动。当我们需要将一个数据 a 插入到已排序区间时, 需要拿 a 与已排序区间的元素依次比较大小,找到合适的插入位置。找到插入点以后,我们还需要将插入点之后的元素顺序往后移动一位,这样才能腾出位置给元素 a 插入。
对于不同的查找插入点方法(从头到尾、从尾到头),元素的比较次数是有区别的。但对于一个给定的初始序列,移动操作的次数总是固定的,就等于逆序度。
这里借用极客时间上王争老师的图做个说明,为什么移动次数等于逆序度。
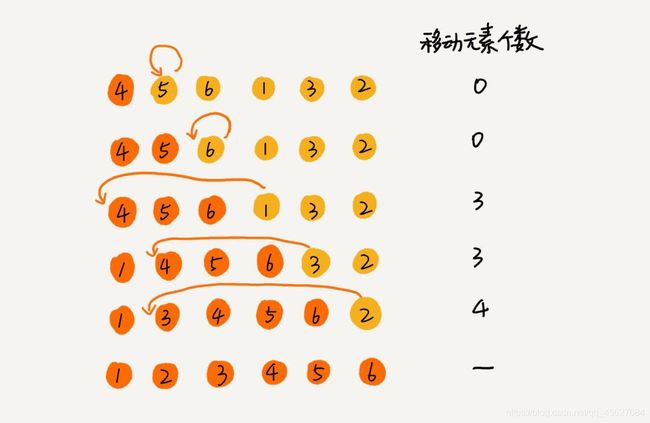
插入排序的代码如下
package com.tyz.about_sort.core;
public class InsertionSort {
public InsertionSort() {
}
public static void insertionSort(int[] arr) {
if (arr.length <= 1) {
return;
}
for (int i = 1; i < arr.length; i++) {
int value = arr[i];
int j = i - 1;
//查找插入位置
for (; j >= 0; j--) {
if (arr[j] > value) {
arr[j + 1] = arr[j];
} else {
break;
}
}
arr[j + 1] = value; //插入数据
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k] + " ");
}
System.out.println();
}
}
}
测试代码如下
package com.tyz.about_sort.test;
import com.tyz.about_sort.core.InsertionSort;
public class Test {
public static void main(String[] args) {
int[] arr = {
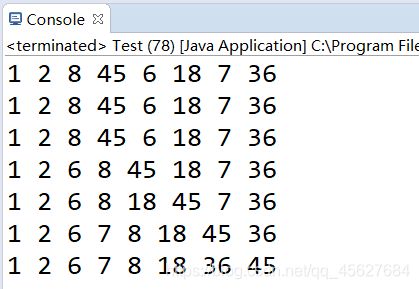
2, 1, 8, 45, 6, 18, 7, 36};
InsertionSort.insertionSort(arr);
}
}
2. 插入排序内存消耗
从实现的过程可以很明显地看出,插入排序算法的运行并不需要额外的存储空间,所以空间复杂度是 O(1),也就是说,这是一个原地排序算法。
3. 插入排序稳定性
在插入排序中,对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是稳定的排序算法。
4. 插入排序时间复杂度
如果要排序的数据已经是有序的,我们并不需要搬移任何数据。如果我们从尾到头在有序数据里面查找插入位置,每次只需要比较一个数据就能确定插入的位置。所以这种情况下,最好时间复杂度为 O(n) 。注意,这里是从尾到头遍历已经有序的数据。
如果数组是倒序的,每次插入都相当于在数组的第一个位置插入新的数据,所以需要移动大量数据,所以最坏情况时间复杂度为 O(n2)。
我们在数组中插入一个数据的平均时间复杂度是 O(n)。所以,对于插入排序来说,每次插入操作都相当于在数组中插入一个数据,循环执行 n 次插入操作,所以平均时间复杂度为 O(n2)。
5. 拓展-希尔排序(Shell Sort)
① 详解
插入排序的弊端是比较明显的,就是只有在数据规模小或者数据基本有序的条件下,插入排序才是高效的。所以在实际应用中,插入排序就很受限制。因此,希尔排序就闪亮登场了。作为插入排序的优化算法,希尔排序对较大规模以及无序的数据集也很有效率。
下面我努力讲清楚希尔排序的核心思想。
我们知道插入排序的弊端是数据集大或者无序性强,那么我们就要解决这个问题,思路就是分而治之,这个思想我在我的程序员必修数学课里写过,有兴趣的同学可以跳转去看看。
【程序员必修数学课】->基础思想篇->递归(下)->分而治之&从归并排序到MapReduce
既然数据量大,那么我们就把它分成一块一块最小的,分成一个数据一个组就没什么意义了,因为希尔排序的本质还是插入排序,所以我们先把一组数据分成两个一组,再对每个组进行排序。这样整个数组的有序性就增加了。接着我们再增加一个组的数据数,分成更大的组,再次对每个组进行排序,然后整体的有序性就又增加了。
就这样重复这个步骤,直到整体的有序性已经到非常大了,这时候再对整体的数据做一次插排,就完成了希尔排序。
这么说还是很抽象,我通过几张图来复盘一下这个过程。
首先先把较大的数据集进行第一次分组。
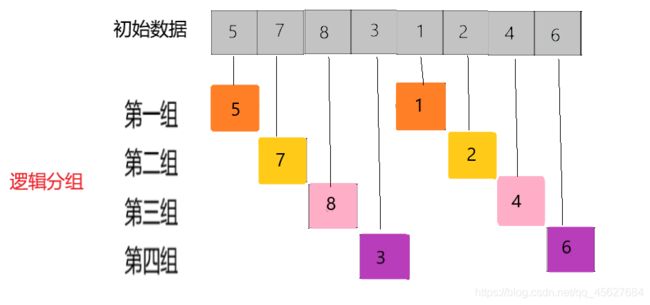
可以看到,我是按下标相隔距离为 4 分的组,a[0] 和 a[4]是一组等等,这里的差值(距离)被称为 增量。所以希尔排序又称缩小增量排序。
接着,我们对每一个组里的数据做一个插入排序,这样每个组就是有序的了。
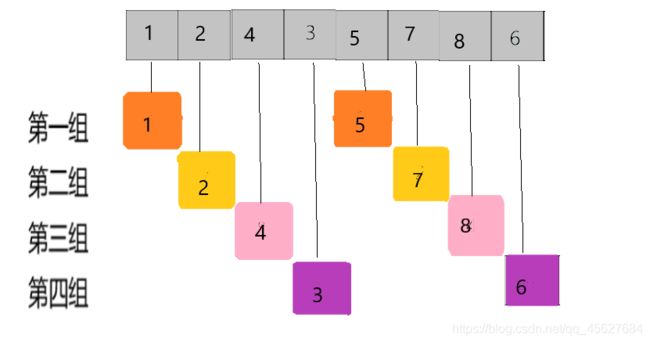
这时整个数组的有序程度就变高了。
接下来再将增量缩小到一半,第一次的增量是 4 ,第二次的增量就为 2,然后再重复上面的步骤,每组做一个插入排序。接着再缩小增量到之前的一半,即为 1,这时候相当于已经没有分组了,经过了前两轮的分组,这时候数组整体上的有序性已经很高了,所以可以直接进行插入排序。
这就是希尔排序的思路。代码实现如下
package com.tyz.about_sort.core;
public class ShellSort {
public ShellSort() {
}
public static void shellSort(int[] arr) {
int length = arr.length;
for (int gap = length / 2; gap > 0; gap /= 2) {
for (int index = gap; index < length; index++) {
insertionSort(arr, gap, index);
}
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k] + " ");
}
System.out.println();
}
}
private static void insertionSort(int[] arr, int gap, int index) {
int value = arr[index];
int j;
for (j = index - gap; j >= 0 && value < arr[j]; j -= gap) {
arr[j + gap] = arr[j];
}
arr[j + gap] = value;
}
}
测试代码如下
package com.tyz.about_sort.test;
import com.tyz.about_sort.core.ShellSort;
public class Test {
public static void main(String[] args) {
int[] arr = {
5, 7, 8, 3, 1, 2, 4, 6};
ShellSort.shellSort(arr);
}
}
② 希尔排序内存消耗
由于希尔排序是插入排序的改良算法,所以希尔排序也不需要额外的空间,是一个原地排序。
③ 希尔排序稳定性
虽然插入排序是稳定的,但是由于希尔排序在插入时是跳跃性插入的,有可能破坏稳定性,所以希尔排序是不稳定排序。
④ 希尔排序时间复杂度
希尔排序的时间复杂度是极其复杂的,它是一个增量序列的排序,而有的增量序列的时间复杂度至今也没有人能证明出来,所以在这里我不再做分析。
Ⅴ 选择排序(Selection Sort)
1. 详解
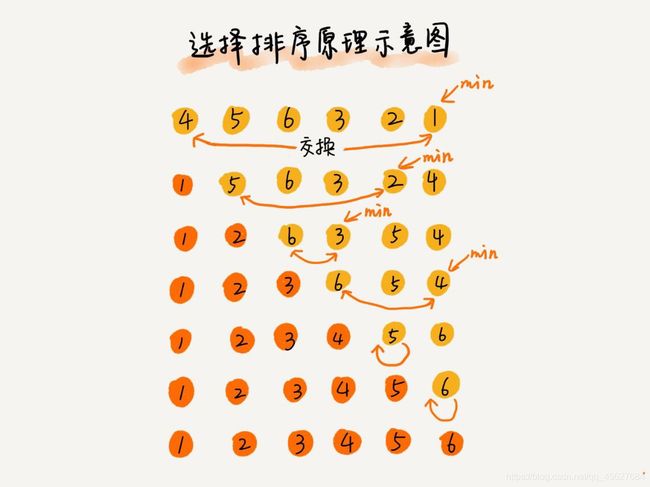
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
package com.tyz.about_sort.core;
public class SelectionSort {
public SelectionSort() {
}
public static void selectionSort(int[] arr) {
int minIndex;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = minIndex = i; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
if (minIndex != i) {
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k] + " ");
}
System.out.println();
}
}
}
测试代码如下
package com.tyz.about_sort.test;
import com.tyz.about_sort.core.SelectionSort;
public class Test {
public static void main(String[] args) {
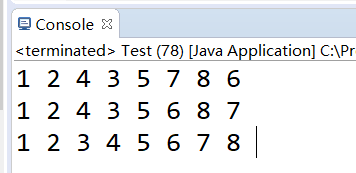
int[] arr = {
4, 5, 6, 3, 2, 1};
SelectionSort.selectionSort(arr);
}
}
2.选择排序内存消耗
同样的,选择排序没有占用额外的存储空间,空间复杂度为 O(1),是一种原地排序算法。
3.选择排序稳定性
选择排序是一种不稳定的排序算法,从前面的图中可以看到,选择排序每次都要找剩余未排序元素中的最小值,并和前面的元素交换位置,这样就破坏了稳定性。
4.选择排序时间复杂度
不管排序的序列为何,每一次进行选择排序都要遍历未排序的数列,并且找到最小的,然后和前面的元素交换位置,所以选择排序不存在最好情况和最坏情况,它的时间复杂度都为 O(n2)。
Ⅵ 为什么插入排序比冒泡排序更受欢迎?
经过前面的学习,我们知道插入排序和冒泡排序的时间复杂度相同,都是 O(n2),但是插入排序却比冒泡排序更受欢迎,这是为什么呢?
在前面我们分析冒泡排序和插入排序的时候说到,冒泡排序不管怎么优化,元素交换的次数都是一个固定值,是原始数据的逆序度。插入排序也是一样的,无论怎么优化,元素移动的次数也等于原始数据的逆序度。
但是,从代码实现上来看,冒泡排序的数据交换要比插入排序的数据移动要复杂,冒泡排序需要三个赋值操作,而插入排序只需要一个。
我们对比一下这个代码。
//冒泡排序中数据的交换操作
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
isChanged = true;
}
}
//插入排序中数据的移动操作
if (arr[j] > value) {
arr[j + 1] = arr[j];
} else {
break;
}
我们把执行一个赋值语句的时间粗略地计为单位时间(unit_time),然后分别用冒泡排序和插入排序对同一个逆序度是 K 的数组进行排序。用冒泡排序,需要 K 次交换操作,每次需要 3 个赋值语句,所以交换操作总耗时就是 3 * K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。大家可以自行做实验验证,在数据量大的条件下,插入排序是比冒泡排序快很多的。
因此,虽然冒泡排序和插入排序在时间复杂度上是一样的,都是 O(n2),但是如果我们希望把性能优化到极致,那肯定首选插入排序。