自幂数9位数查找之算法优化（C语言）（水仙数是4位数自幂数）

``# 自幂数的9位数查找之算法优化（C语言）
这是一篇C语言有关自幂数查找的优化过程，目前笔者最好结果是8位数用时7.007秒，9位数用时79.079秒。（水仙数是4位数自幂数）
期待有更棒的结果。

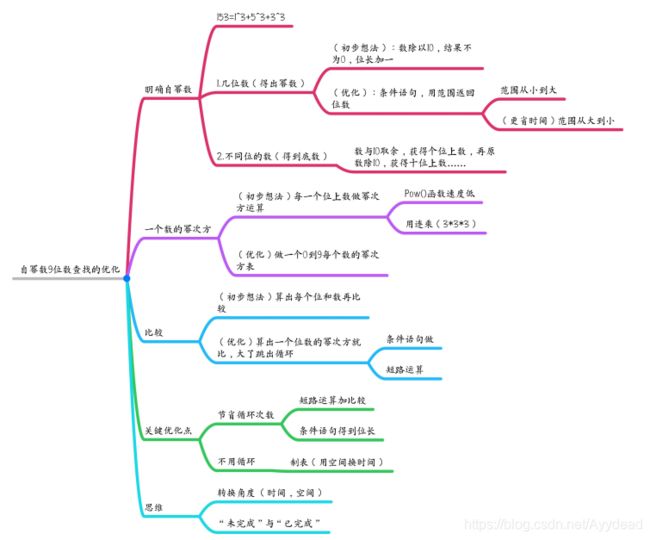
思维导图先上！！！

一，明确自幂数

1.什么是自幂数？

自幂数是指一个 n 位数，它的每个位上的数字的 n 次幂之和等于它本身。（水仙数是4位数自幂数）
（例如：当n为3时，有1^3 + 5^3 + 3^3 = 153，153即是n为3时的一个自幂数）

2.关键点。

1）幂数（自幂数的位数）

2）各底数（自幂数的每个位上的数）

3）一个数的幂次方

4）求和比较

二，一个数的幂次方

1.得到幂数

1）初步想法：

1.这个数除以10赋值给自己：
2.这个数为0，跳出循环。
3.这个数不为0，位长加1，执行第一步。

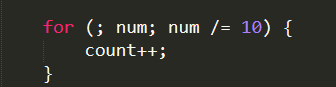
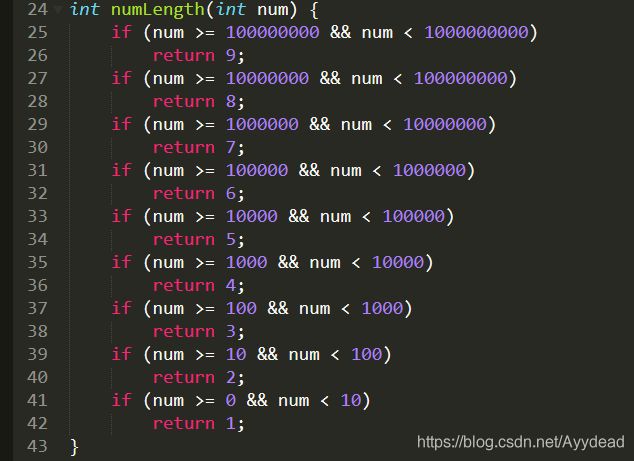
2）优化： 打破循环，直接用条件语句判断范围完成。

这里有一个很棒的优化点。
例如：一般都会从0开始。

但是，这样效率并不高，每次查找9位数都得先经过前面的1到8位数的判断，而先判断9位数会则减少时间，尤其1位数的个数少，全部经历8次判断次数的总次数远远少于9位数在底下的情况。如下：

wow,皮卡丘你好棒！！！

2.得到底数

这个简单，原数与10取余，保存余数，接着除以10，继续取余。
代码在后面附上.。嘤嘤嘤…

3.一个数的的幂次方

1）初步想法：

每一个位上的数做幂次方运算。
例如：153这个数， 求出1^3 ， 5^3 ， 3^3 ， 而且不推荐用pow()函数，因为pow()可以运算1.25 6^5.632 这么复杂的数，其运算1^3时间 绝对比1* 1* 1要长。
这个代码就算了吧，可达鸭表示饿了。

2）优化：用空间换取时间

发现如果用for循环，在取得底数时直接做幂次方运算，例如这样

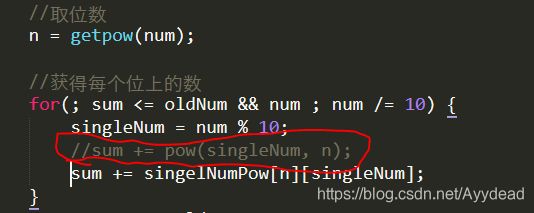
会很浪费时间，555596，这个数中5的6次方会做4次，其中后三次没有必要。
所以建立一个0~9的数字幂方表。很有用。
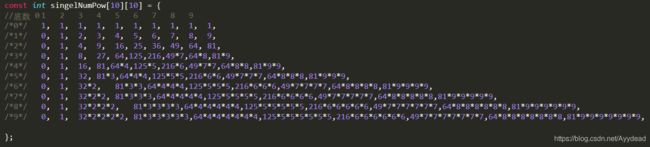笔者提醒你，表格要写对。错了一数字，程序两行泪。

三，求和与比较

1）初步想法：

算出每一个数的幂次方求和后再比较。
上图：

2）优化： 1.未完成也可以比较

这时候聪明的你，肯定想到把if语句放进循环里，再给它来个啥break; 或者return；直接跳出循环。

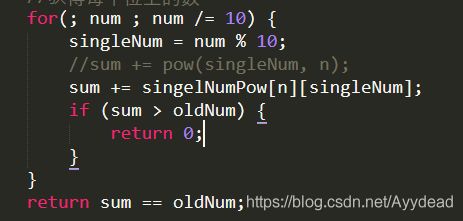
等一等，似乎可以优化下。

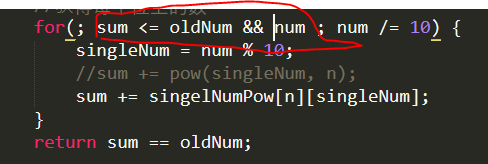
你发现了大秘密，短路运算 ！！恭喜你获得经验+1 。

四，使用

保佑保佑，快来保佑我。代码走起来，走起来。

失败…嘿嘿怎么不可能，少了一个；
磨人的小妖精！！继续。
忘了说一句使用time库，计时哦！！
最后，8位数用时7.007秒。

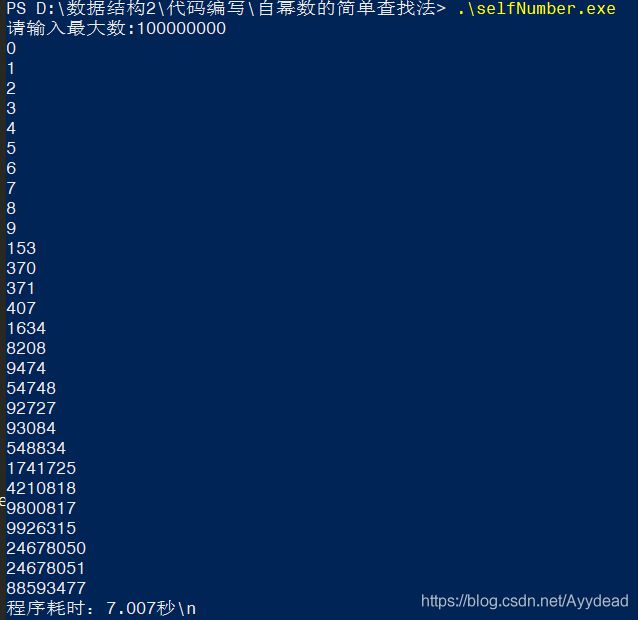
9位数用时79.079秒。

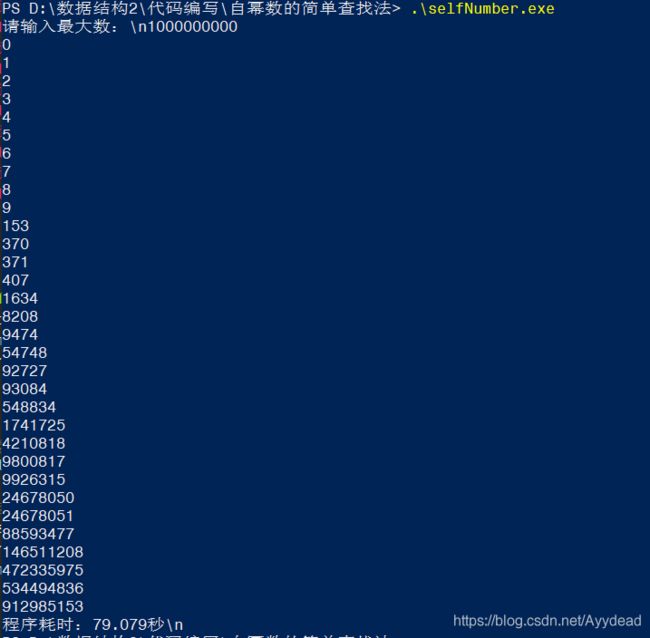
可以试试所有初步想法运行，也许你可以睡一会，让电脑加油。
完结散花☺☺☺

五，总结

笔者认为两个关键点：
1.空间换取时间
2.未完成与已完成。

一些小技巧的运用可以大大节省时间。
笔者斗胆认为，编程函数分而治之是做这个题目更重要的。
做好分析，手工过程，再上手，再优化。
编程有时也像画画。

感谢指导老师：铁血教主
笔者水平有限，目前只能描述以上问题，如果有其他情况，可以留言，有错误，请指教，有继续优化的，请分享，谢谢！

源码过段时间上传。

2019年11月26日 图书馆

#include 

#include 


const int singelNumPow[10][10] = {
//底数 0	1	2	3	4	5	6	7	8	9
/*0*/	1,	1,	1,	1,	1,	1,	1,	1,	1,	1,		
/*1*/	0,	1,	2,	3,	4,	5,	6,	7,	8,	9,	
/*2*/  	0,	1,  4,  9,	16,	25,	36,	49,	64,	81,	
/*3*/   0,	1, 	8,  27,	64,125,216,49*7,64*8,81*9, 
/*4*/   0,	1,	16,	81,64*4,125*5,216*6,49*7*7,64*8*8,81*9*9,
/*5*/   0,	1,	32,	81*3,64*4*4,125*5*5,216*6*6,49*7*7*7,64*8*8*8,81*9*9*9,
/*6*/   0,	1,	32*2,	81*3*3,64*4*4*4,125*5*5*5,216*6*6*6,49*7*7*7*7,64*8*8*8*8,81*9*9*9*9,
/*7*/   0,	1,	32*2*2,	81*3*3*3,64*4*4*4*4,125*5*5*5*5,216*6*6*6*6,49*7*7*7*7*7,64*8*8*8*8*8,81*9*9*9*9*9,
/*8*/   0,	1,	32*2*2*2,	81*3*3*3*3,64*4*4*4*4*4,125*5*5*5*5*5,216*6*6*6*6*6,49*7*7*7*7*7*7,64*8*8*8*8*8*8,81*9*9*9*9*9*9,
/*9*/   0,	1,	32*2*2*2*2,	81*3*3*3*3*3,64*4*4*4*4*4*4,125*5*5*5*5*5*5,216*6*6*6*6*6*6,49*7*7*7*7*7*7*7,64*8*8*8*8*8*8*8,81*9*9*9*9*9*9*9,
	
};


char isSelfNumber(int num);
int getpow(int n);
/*int singelNumPow(int singleNum, int n);
int singelNumPow(int singleNum, int n) {

}*/

int getpow(int num) {
	if (num >= 100000000 && num < 1000000000)
		return 9;
	if (num >= 10000000 && num < 100000000)
		return 8;
	if (num >= 1000000 && num < 10000000)
		return 7;
	if (num >= 100000 && num < 1000000)
		return 6;
	if (num >= 10000 && num < 100000)
		return 5;
	if (num >= 1000 && num < 10000)
		return 4;
	if (num >= 100 && num < 1000)
		return 3;
	if (num >= 10 && num < 100)
		return 2;
	if (num >= 0 && num < 10)
		return 1;
	
}

char isSelfNumber(int num) {
	int oldNum;
	int sum = 0;
	int singleNum;
	int n;

	oldNum = num;
	//取位数
	n = getpow(num);

	
	//获得每个位上的数
	for(; sum <= oldNum && num ; num /= 10) {
		singleNum = num % 10;
		//sum += pow(singleNum, n);
		sum += singelNumPow[n][singleNum];	
	}
	return sum == oldNum;
	
}

int main() {
	int Maxnum;
	int ok;
	int i;
	long startTime;	
	long endTime;

	printf("请输入最大数:");
	scanf("%d",&Maxnum);
	startTime = clock();
	for ( i = 0; i < Maxnum ; i++) {
		//遍历查找，成功返回
		ok = isSelfNumber(i);
		if (1 == ok) {
			printf("%d\n",i);
		}
	}
	endTime = clock();
	endTime -= startTime;
	endTime /= 1000;
	printf("程序耗时：%ld.%03ld秒\n", endTime, endTime % 1000);


	return 0;
}