字符串匹配算法：蛮力算法、KMP算法、BM算法

概念定义

1. 子串：字符串中任一连续的片段，称作其子串（substring）
2. 前缀：prefix(S, K) = S.substr(0, K) = S[0, K)
3. 后缀：suffix(S, K) = S.sbustr(n-K, K) = S[n-k, n)
4. 串模式匹配（string pattern matching）：
   对基于同一字符表的任何文本T（|T| = n）和模式串P（|P| = m）:
      - 判定T中是否存在某一子串与P相等
      - 若存在（匹配），则报告该字串在T串的起始位置

蛮力算法（Brute force）

算法1：

int match(char* P, char* T) {
    size_t n = strlen(T), i = 0;
    size_t m = strlen(P), j = 0;
    while(i < n && j < m) {
        if(T[i] == P[j]) {
             ++i; ++j;
        }
        else {                    //失配
            i = i - j + 1;        //文本串回退j-1个字符
            j = 0;                //模式串置零
        }
    }
    return i - j;                 //当(i-j)>m时，发现匹配，且P相对于T的对齐位置为i-j
}

算法2：

int match(char* P, char* T) {
    size_t n = strlen(T), i = 0;
    size_t m = strlen(P), j = 0;
    for( i=0; i

分析

   算法1与算法2都是比较直观的算法，其时间复杂度均为O(n²)，但这两种算法会与KMP算法以及其改进算法的架构类似。

KMP算法

算法策略

   KMP算法在于借助对比经验，在每次模式串P向右平移时，能够大步向前而非亦步亦趋。

   借助以上邓老师书上的图，试图解析一下KMP算法的策略。
   假设这是文本串T与模式串进行匹配的某个时刻的快照，且此时在T[i] 与P[j] 处发生了失配；同时，假设我们此时将P向右移动j-t个字符后，在t处再次得到：P[0, t) == T[i-t, i)，即下图的黄色标记的两段：

   如此，我们可以一次将P右移t步，那么，t准确地应该取多少呢？经过前一轮的比对，已经确定匹配的范围为：
$$P[0,j)=T[i-j,i)$$
   移动t步后得到：
$$P[0,t)=T[i-t,i)=P[j-t,j)$$
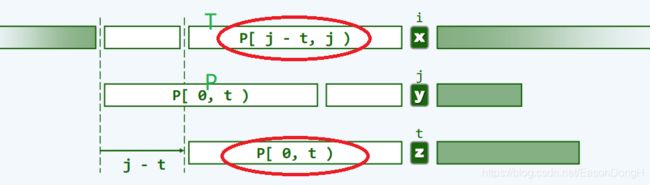
   如上图，很容易观察到P[0, t)与P[j-t, j)其实就是以t为分界点，划分得到的真前缀、真后缀，亦即，在P[0, j)中长度为t的真前缀，应与长度为t的真后缀完全匹配，故t必来自集合：
$$N(P,j)=\{0\le t<j|P[0,t)=P[j-t,j)\}$$
   一般地，该集合可能包含多个这样的t，但需要注意的是，其中具体有哪些t构成，仅取决于模式串P以及前一轮比对的首个失配位置P[j]，与文本串T无关。

KMP算法实现（C++）

int KMP(char* P, char* T) {
	int* next = buildNext(P);
	int n = (int)strlen(T), i = 0;
	int m = (int)strlen(P), j = 0;
	while (i < n && j < m) {
		if (j < 0 || T[i] == T[j]) {
			++i; ++j;
		}
		else
			j = next[j];
	}
	delete[] next;
	return i - j;
}

   与蛮力算法1相比，仅失配时算法有所区别：KMP算法此时保持i不变，从next表中取出一个j来代替置零。注意if判断条件多了一个0

int* buildNext(char* P) {
	size_t m = strlen(P), j = 0;
	int* N = new int[m];
	int t = N[0] = -1;
	while (j < m - 1) {
		if (t < 0 || P[j] == P[t]) {
			++j; ++t;
			N[j] = t; //此处可改进
		}
		else
			t = N[t];
	}
	return N;
}

   可以看到，我们统一将N[0]赋值为-1，此处可假定在P[0]前面有一个哨兵，该哨兵是一个通配符，遇其必然进入if分支，该处相当于整个P在T[i]都没有匹配的位置，因此要将P移动|P|步，并将i向右移动1步，即：

   因此可以解释为何KMP算法中if判断条件为何多了一个。至此，我们简单分析完了KMP算法的策略与算法实现，在buildNext代码中，我们可以进一步优化，可改写其为：

N[j] = (P[j] != P[t] ? t : N[t]);

   其原因与正确性暂且不表。

KMP算法性能

   我们仅需将目光放在算法的循环部分：

    while (i < n && j < m) {
		if (j < 0 || T[i] == T[j]) {
			++i; ++j;
		}
		else
			j = next[j];
	}

   引入k = 2*i - j，对于if分支，i、j必然同时+1，则k必然会+1；对于else分支，i不变，next[j]必然至少会比j小1，则k至少也+1因此，k具有单调递增的特性。再考虑最后k的范围，其初始值为0，循环结束后有：
$$k=2\ast i-j\le 2\ast (n-1)-(-1)=2n-1$$
   则得出结论，k单调递增，且最大至O(n)；算上buildNext所需要的时间，则KMP算法时间复杂度为O(n+m)。

BM算法

介绍

BM算法中依然是将模式串P与文本串T从左开始对齐，但是却是自模式串的右边向左边进行扫描对比。为实现高效率，BM算法同样是充分利用以往的信息，使得P可以“安全的”往后尽可能多的移动。

主体框架

int BM(char* P, char* T) {                //Boyer-Morre算法
	int* bc = buildBC(P);
	int* gs = buildGS(P);
	size_t i = 0;                                  //模式串相对于文本串的起始位置（初始时与文本串左对齐）
	while (i + strlen(P) <= strlen(T)) {
		int j = strlen(P) - 1;                   //从模式串的末尾字符开始对比
		while (P[j] == T[i + j])
			if (--j < 0)
				break;
		if (j < 0)                                       //已经完全匹配
			break;
		else                                             //否则，适当地移动模式串
			i += max(gs[j], j - bc[T[i + j]]);//位移量根据BC表和GS表选择最大者
	}
	delete[] gs;
	delete[] bc;
	if (i + strlen(P) <= strlen(T))
		return i;
	else
		return -1;
}

坏字符与好后缀

BM算法通过提前计算坏字符与好后缀的情况，从而在遇到时进行尽可能多的移动。

int* buildBC(char* P) {
	int* bc = new int[256];
	for (size_t j = 0; j < 256; ++j)
		bc[j] = -1;
	for (size_t m = strlen(P), j = 0; j < m; ++j)
		bc[P[j]] = j;//画家算法：用后来值覆盖前者
	return bc;
}

int* buildGS(char* P) {//构造好后缀位移量表：O(m)
	int* ss = buildSS(P);
	size_t m = strlen(P);
	int* gs = new int[m];
	for (size_t j = 0; j < m; ++j)
		gs[j] = m;
	for (size_t i = 0, j = m - 1; j < UINT_MAX; --j) {//逆向逐一扫描个字符P[j]
		if (j + 1 == ss[j]) {//若P[0,j] = P[m-j-1,m)，则
			while (i < m - j - 1)//对于P[m-j-1]左侧的每个字符P[i]而言
				gs[i++] = m - j - 1;//m-j-1都是gs[i]的一种选择
		}
	}
	for (size_t j = 0; j < m - 1; ++j)
		gs[m - ss[j] - 1] = m - j - 1;
	delete[] ss;
	return gs;
}

int* buildSS(char* P) {//构造最大匹配后缀长度表：O(m)
	int m = strlen(P);
	int* ss = new int[m];
	ss[m - 1] = m;//对最后一个字符而言，与之匹配的最长后缀就是整个P串
	//以下：从倒数第二个字符起自右向左扫描P，依次计算出ss[]其余各项
	for (int lo = m - 1, hi = m - 1, j = lo - 1; 0 <= j; --j) {
		if ((lo < j) && (ss[m - hi + j - 1] <= j - lo))
			ss[j] = ss[m - hi + j - 1];
		else {
			hi = j; lo = min(lo, hi);
			while ((0 <= lo) && (P[lo] == P[m - hi + lo - 1]))
				--lo;
			ss[j] = hi - lo;
		}
	}
	return ss;
}

总结

如下图，得出以上几种算法的性能分析。