字符串匹配 蛮力搜索 KMP BC GS 数据结构Trie by邓俊辉老师

字符串string：一连串的字符连在一起。是一种线性序列。仅能存储字符集。

特点：

1. 非常长、比一般的线性序列长一些。只能存储字符集。
2. 经常采用连续的一段pattern进行比对。也就是call by pattern 根据模式进行访问。

经常在字符串的前后加上一个假想的哨兵，优化算法
子字符串S.substr(i,k)=S[i,i+k） 左闭右开。一共k个字符 注意substring 子字符串 与 subseqence 公共子串 不同 前者更多是一些切片slice，后者就是一些子串。
substring的特例：前缀S.prefix(k)=S[0,k)和后缀S.suffix(k)=S[n-k,k)
$\text{S.substr}(i,k)=\text{ S.prefix }(i+k).\text{ suffix }(k)=\text{ S.suffix }(n-i).\text{ prefix }(k)$

PM pattern matching 字符串匹配。

$2\ll m\ll n$
text: 长度为 n=|T|
pattern：长度为 m=|P|

PM: brute force 蛮力搜索

一共有n-m个位置，逐个去尝试。
最好的情况(更常规的情况，每个地方上来就发现错误) $\Omega (n)$
最坏的情况 每一个都要对齐到pattern的最后位置。 $\mathcal{O}(n\cdot m)$

version #1 :

int match( char * P , char *T ){
	size_t n = strlen(T), i=0;  		//i为T中的指针
	size_t m = strlen(P), j=0;		//j为P中的指针
	while( j < m && i < n ) //自左向右逐次比对
		if( T[i]==P[i] ) {i++;j++;}  //若匹配则转到下一对字符
		else					{ i -= j-1; j = 0;} //否则,T回退、P复位
	return i-j;
	//如果匹配成功，则会返回P相对于T的对齐位置i-j。
	//如果匹配失败的话则返回的i-j必然在T的最后m个位置中。
}

version #2:

int match( char * P , char *T ){
	size_t n = strlen(T), i=0;  		//i为起始的位置
	size_t m = strlen(P), j;			//j为P中的指针
	for( i = 0; i < n-m+1; i++ )	{	//T[i]与P[0]对齐后
		for( j=0; j

注意：python的for 循环可以执行else。else 是否执行取决于for循环是否正常耗尽。（退出多层循环）

burte force 每次只排除一个位置比较慢，下面介绍更优的方法

PM: Good Prefix + Look-up Table KMP算法

KMP是三位学者的姓名的首字母连起来。
经过j次比较，不仅仅知道P中的元素，也知道T中进行比对过的元素。
对pattern串实现记录一些信息。如果失配的话，应该把下一步需要对齐的字符的序号放在失配处对应的table中。对T中的元素进行打表，每次不对齐。

首字符比对失败时，其table值为通配符是-1； 也就是再挪动一格。

int match( char * P, char * T ){
	int * next =buildNext(P);  
	int n = (int)strlen(T), i=0;
	int m = (int)strlen(P), j=0;
	while( jj || T[i]==P[j] ){   // j为负数时存在短路特性  保证通配符-1
			i++; j++;
		}else
			j = next[j];  //next表说明接下来应该和谁对齐
	delete[] next;
	return i-j;
}

KMP算法的比对是没有重复的。时间复杂度O(n)

next表的生成方法
注意next[0]恒等于-1;是一个通配符。
如何构造next表？ incremental strategy 递增策略。
如何第j项算完以后计算第j+1项。
next[j+1] = next[j]+1 iff P[j]=P[next[j]]; //iff指当且仅当
如果不相等了，那么每次寻找next of next

int * buildNext( char * P ){
	size_t m = strlen(P),j=0;
	int *N = new int[m]; 
	int t = N[0] = -1;
	while( jt || P[j]==P[t] ) ? N[++j] = ++t : t=N[t];  // j为负数时存在短路特性  保证通配符-1.注意t>N[t]
	return N; 
}

快速滑动、绝不回退
能否跑到线性呢? 在某个位置上可能进行多次回退（多次next）。这种现象叫做分摊。存在最坏的情况但不会频繁发生所以可以分摊，复杂度仍然为线性的。
证明KMP复杂度为O(n):（Amortization分摊）
令 k= 2*I - j k必然随着迭代而单调递增，也就是迭代步数的上界。 case1相等ij同时加1，case2 i变，j=N[j]变小。 k最多是两倍N。

KMP：improvement
重复的next of next 如何改进呢？

int * buildNext( char * P ){
	size_t m = strlen(P),j=0;
	int *N = new int[m]; 
	int t = N[0] = -1;
	while( jt || P[j]==P[t] ){
			j++; t++; N[j] = (P[j] != P[t]) ? t : N[t];
		} else
			t=N[t]; 
	return N; 
}

注意即便此时核对P[j]==P[t] 成功了，那么需要核对P[j]与P[t] (j、t加一后)是否相等。入伙相等则直接将N[t]直接复制给N[j];

PM 之 BC: bad character

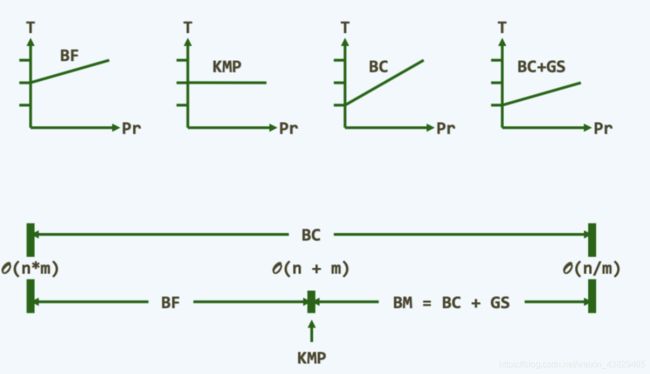
TP的比对依然是从左往右推移，但是在每一对准位置却是自右向左地逐一比对各字符。
以终为始，先去判断靠后的错误。可以排除掉远比刚才更多的潜在的不可能位置。
Bad Character Shift：
shift的量要足够小。x要取最靠右的那个。有最后后缀不包含x。
寻找坏字符x。
有时候寻找不到x。那么令bc[x]=-1 设置成为通配符。
有时候有时候最右的那个x，会使shift小于0（j

construct BC表。 记录character出现的位置。没有出现的初始化为一个undefined

int * bulidBC( char * P ){   //O(s+m)
	int * bc = new int[256]; 
	for(size_t j=0; j<256; j++) bc[j]=-1;
	for(size_t m=strlen(P),j=0; j

初始化一个BC表为-1即通配符。从头到尾扫尾一次m。如果出现了多次的字符，则会希望留下最右边的（最大的）。
这种策略叫做画家策略。 painter’s 油画家可以看到的最上层的油色。
BC表的大小。就是字符集的大小。 也就是从-1开始匹配

最好的情况是 O(n/m) 。最坏的情况是O(n*m)。

PM之 GS： good suffix shift

GS与kmp类似。
好后缀，

复杂度分析（实际上BF基本上复杂度大概率也线性的）

KMP举例时 101101100或者abccbaac 因为二个的字符表为2，三个的字符表为3.误入歧途的概率比较大。
如果字符比较多的话，其实误入歧途的概率也比较小。此时KMP与BF复杂度也差不多。
在编写教材的时候，为凸显KMP算法的优点，字符种类数目都会比较小。

数据结构 之 Trie = Digital Tree = Radix Tree

前缀树，数字数。 retrieval:检索 从中取了四个字母 为与tree以示区别，读作try (ai)
用于操作引擎。根据前缀进行查找。
26个字母26个分支。最后截止于terminal。
注意第一个根节点不存放内容。
改进一：PATRICIA Trie 。 对于单分支的可以将一个子串全部置于某个节点下。
改进二：对于多分支的，可以归一化整理为一个三叉的树。ternary tree