【应用C】C语言实现离散数学合式公式的递归判断
实现合式公式的递归判断,是大二离散数学老师给我们出的一道编程题,当时也是第一次接触递归,苦思冥想一段时间后写出来了,逻辑应该没多大问题,也测试过一组数据,应该还有BUG,希望有人提醒我,在此分享给各位。
完整的代码:百度网盘(包含了加括号)
在CSDN上搜一搜,发现还是有挺多合式公式的判断,不过很多都是循环暴力破解,虽然有递归,不过代码逻辑不太清晰,描述较少,小白严格按照定义去实现合式公式的判断。
我所用的离散数学书本中合式公式定义如下图:

为了能够在键盘上方便获得联结词,你我约定:
| 联结词 | 键盘 |
|---|---|
| ﹁ | !(感叹号) |
| ∧ | *(乘号) |
| ∨ | +(加号) |
| ↔ | =(等号) |
| → | -(减号) |
这个定义可能和百度百科的定义不同,百度百科的定义中多了一条量词判断,也就是:若A是合式公式,x是A中的变量符号,则∀xA和∃xA也是合式公式; 其实多一条不要紧,修改也很容易,无非是多一个判断前导字符是不是∀x或者 ∃x而已,因此小白还是按照上图中的定义去编写代码,额外的判断以及后面的真值表留给各位自行发挥。
可以看出合式公式的定义是递归定义,也就是在定义中又使用了定义,因此编写判断代码也应该是递归的,首先要分清标准合式公式和非标准合式公式(为什么有标准和非标准,因为人很懒,不想写括号)。

标准合式公式: 严格按照定义的合式公式。 要注意到“严格”两个字,数学上的严格是不允许有一点差错的,必须是十全十美的(数学上能称作标准的东西都是非常正规正矩的,对强迫症者而言是个福音)。
非标准合式公式: 在标准的合式公式基础上省略了括号。 没错,就是因为人很懒,不想写括号,就称作非标准的合式公式,非标准不是错误的意思,而是它并不严格符合定义而已,只要加上括号后又是一个标准的合式公式。
觉得非常生涩?举个例子,!a是非标准,而(!a)是标准,a*b+(!c) 是非标准,而((a*b)+(!c))是标准。日常生活中,写比较短的公式我们一般都是不会加括号的,但是不能否认它不是公式。
判断合式公式(WWF)
既然有标准和非标准之分,那么编程的时候是否需要区分?答案是不需要,上文提到,非标准只是省略了括号,只要人为添加括号就是一个标准合式公式了,所以先把精力放在标准合式公式上面,抽象出定义,其实合式公式只有三类:a、(!A) 、(A@B)。a称为原子命题(只有1个字母),如果稍微知道一点递归,可以知道a就是递归的出口,(!A)使用了单目运算,(A@B)使用了双目运算。
在编写算法之前,我们确定一下人是怎样判断出合式公式的,其实是按照定义一条一条匹配的,举个例子,对于(a*b),应该怎么判断?
判断过程:
1、根据定义①可知,(a*b)不是原子命题,进入2。如果是原子命题,返回真,结束判断,如果长度是1但不是字母,返回假,结束判断。
2、根据定义②,我们只关心!A,去掉(a*b)的最外层括号,得到a*b,寻找联结词,得到*,并不是!,因此不是(!A)类型,进入3。如果联结词是!,需要继续判断A,让A进入1。
3、根据定义③,我们只关心A@B,把A、B分离,同时进行判断,只有A和B同时是合式公式,才能得出A@B是合式公式,所以结果进行与(&&)运算。去掉(a*b)的最外层括号,寻找联结词,(a*b)中可以得出A=a,B=b,双目运算符@=*,分别让A和B进入1,结果进行与运算,如果运算后为真,(a*b)是合式公式,否则不是合式公式。
……
分别让A和B进入1就不再累述,a和b都是原子命题,返回真,结果相与为真,所以(a*b)是合式公式。
这个过程很像剥洋葱,如果公式足够复杂,会一层一层把括号去掉,进入下一层,直到遇到不能再剥开为止,不能再剥开的就是原子命题,它就是递归的出口。

根据这个过程,我们可以总结出一些核心步骤:判断原子命题、去括号、找联结词、递归调用,可以先写出伪代码:
bool separate()
{
if( is_atom() )
return true;
delete_bracket();
if( !find_operator() )
return false;
return separate();
}
程序的架构已经出来,接下来就是一个个函数去实现以及细节问题,is_atom()和delete_bracket()都好写,关键是find_operator(),如何从!A 或者A@B中寻找联结词!或者@,我们注意到,A@B中@的左边A是一个公式,而所有的数学公式左右括号的数量都必定相等,因为括号是成对出现的,不会单个出现,根据这个,我们就能把A@B从左往右遍历,利用一个标识变量flag,遇到左括号加1,遇到右括号减1,当flag==0的时候,我们就遍历到了一个公式,对于!A也一样,只是需要判断一下当前位置是否为!即可。
所以,find_operator()伪代码如下:
bool find_operator(char *str,int begin,int end)
{
int flag = 0;
for( i = begin ; i<=end; i++)
{
if(str[i]=='(') flag++;
if(str[i]==')') flag--;
if(flag == 0)
{
if( is_operator(str[i+1]) ) //A@B
{
save position = i+1;
return true;
}
else if( is_operator(str[i]) ) //!A
{
save position = i;
return true;
}
else
{
return false;
}
}
}
return false;
}
至于is_operator()函数,只是判断一下是不是我们约定好的联结词,在此就不再贴出。
下面贴出核心分离函数separate,步骤就是我们总结出的核心步骤,而核心步骤是模仿人的思考过程得到。
bool separate(char *str,int begin,int end)
{
if( is_atom(str,begin,end) ) //a
return true;
else //(!A) (A@B)
{
/* 去括号 */
int ibegin = delete_bracket(str,begin,end,left_type);
int iend = delete_bracket(str,begin,end,right_type);
/* 寻找运算符 */
if( (ibegin >= iend) || !find_operator(str,ibegin,iend) )
return false;
/* 递归调用 */
if(save.type == SINGLE) //!A
return separate(str,save.position+1,iend) ;
if(save.type == DOUBLE) //A@B
{
int po = save.position;
return separate(str,ibegin,po-1) && separate(str,po+1,iend);
}
}
}
这样,一个标准的合式公式判断就完成了,以下是一些测试(正确和错误):
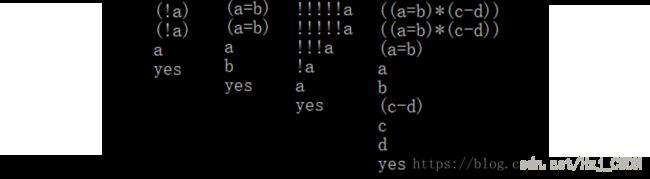
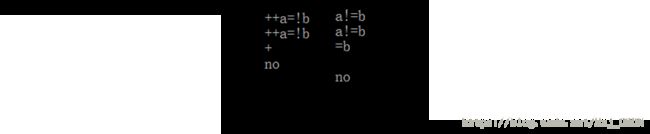
看起来没什么问题。可是!因为人很懒,不想输入这么多括号怎么办?? 我们先不输入括号,看看我们标准的判断是怎样的。
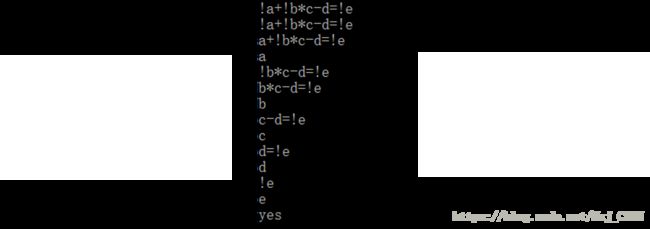
结果虽然是yes,可是过程有一个错误,就是联结词不分优先级,从左往右碰到谁谁就是最高级,虽然这样分也是可以的,不过如果是要作出真值表,这样就是错误的,为了后面能够作出真值表,我们需要根据优先级人为添加括号。
怎么添加就不再说明了,方法很多,我用了最笨的方法,按照!、*、+、-、=的优先级分别添加。
下面是源码的目录:
wwf是标准的合式公式判断,而wwf_plus就是加括号一些函数。
完整的代码:百度网盘(包含了加括号)
文章开头提及到了,百度百科的合式公式定义还有一个量词判断,以及需要作出合式公式的真值表,各位可以在源码基础上修改得到,如果有兴趣编写的,欢迎联系小白。