算法复习
优先队列
q.push(k);//在q的末尾插入k
q.pop();//删掉q的第一个元素
q.top();//返回q的第一个元素
sort
默认从小到大排序
bool cmp(node a,node b) //函数名任意取,该函数为bool形
{
if(a.y==b.y) //如果两个结构体的y相同,按它们的x值从小到大排列
return a.x
我习惯保存数组使用下标1—n 此时应为sort(a+1,a+n+1,cmp)
struct
struct Student //不需加typedef
{
int a;
};
于是就定义了结构体类型Student,声明变量时直接Student stu2;
递推
快速模幂a^b%m
int ans = 1, base = a
while(b > 0)
{
if(b & 1)
{
ans *= base;
ans %= m;
}
base *= base;
base %= m;
b >>= 1;
}
分治
#include
#include
long long num_of_pairs = 0;
using namespace std;
int main()
{
void mergesort(int first, int last, vector&v);
void merge(int first, int mid, int last, vector&v);
int num, data;
vector v1;
cin >> num;
for (int i = 0; i < num; i++)
{
cin >> data;
v1.push_back(data);
}//输入数据
mergesort(0, num - 1, v1);
cout << num_of_pairs << endl;
v1.clear();
return 0;
}
void merge(int first, int mid, int last, vector&v)
{
vector temp(last - first + 1);//临时vector用于存放排顺序//的数据
int i = first, j = mid + 1, k = 0;
while (i <= mid&&j <= last)
{
if (v[i] <= v[j])
{
temp[k++] = v[i++];
}
else {
temp[k++] = v[j++];
num_of_pairs += (mid - i + 1);
//归并时,左序列和右序列分别为有序数列,因而若v[i]>v[j]
//则从v[i]...v[mid]均大于v[j],因而v[i]>v[j],可以得到有mid-i+1个逆序对
}
}
while (i <= mid)
{
temp[k++] = v[i++];
}
while (j <= last)
{
temp[k++] = v[j++];
}
for (i = 0; i &v)
{
if (first < last)
{
int mid = (first + last) / 2;
mergesort(mid + 1, last, v);
mergesort(first, mid, v);
merge(first, mid, last, v);
}
}
动态规划
二叉苹果树
int sz[maxn]; 树枝数目
void dfs(int u,int fa){
for(int i=head[u];~i;i=e[i].next){
int v=e[i].to;if(v==fa)continue;
dfs(v,u);sz[u]+=sz[v]+1;
for(int j=min(sz[u],m);j;--j) 倒序01背包
for(int k=min(sz[v],j-1);k>=0;--k)
f[u][j]=max(f[u][j],f[u][j-k-1]+f[v][k]+e[i].w);
}
}
树形dp最大子树和
void dfs(int u,int fa)//u为当前节点,fa为u的爸爸
{
f[u]=a[u]; //先给f[u]赋初值,就是u本身的美观指数
for(int i=head[u];i;i=tree[i].next) //找儿子
{
int v=tree[i].to;
if(v!=fa) //之前加的双向边,可能跑回去
{
dfs(v,u); //继续向下找
f[u]+=max(0,f[v]); //状态转移
}
}
ans=max(ans,f[u]); //更新ans
}
上司下属
void dfs(int root){
14 for(int i=0; i士兵
define mst(s, t) memset(s, t, sizeof(s))
9 const int INF = 0x3f3f3f3f;
10 const int maxn = 1510;
11 int dp[maxn][2], father[maxn];
12 vector G[maxn];
13 void dfs(int root){
14 for(int i=0; i 地图 马拦卒
#include
#include
#include
#include
#define ull unsigned long long
using namespace std;
const int fx[]={0,-2,-1,1,2,2,1,-1,-2};
const int fy[]={0,1,2,2,1,-1,-2,-2,-1};
//马可以走到的位置
int bx,by,mx,my;
ull f[30][30];//f[i][j]代表从A点到(i,j)会经过的线路数
bool s[30][30];//判断这个点有没有马盯着
int main(){
scanf("%d%d%d%d",&bx,&by,&mx,&my);
++bx; ++by; ++mx; ++my;
//坐标+1以防越界
f[1][1]=1;//初始化
s[mx][my]=1;//标记马的位置
for(int i=1;i<=8;i++)
s[ mx + fx[i] ][ my + fy[i] ]=1;
for(int i=1;i<=bx;i++){
for(int j=1;j<=by;j++){
if(s[i][j])continue;
f[i][j]=max( f[i][j] , f[i-1][j] + f[i][j-1] );
//状态转移方程
}
}
printf("%llu\n",f[bx][by]);
return 0;
}
钢管切割-- 一个划分成n个
#include
#include
using namespace std;
const int lenmax =1000+5;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
int t[lenmax];
int dp[lenmax];
int main(int argc, char** argv) {
int n;
while(~scanf("%d",&n))
{
memset(dp,0x3f,sizeof dp);
int i,j;
for(i=1;i<=n;i++)
{
scanf("%d",&t[i]);
}
dp[1]=t[1];
dp[0]=0; //初始化
for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
{
dp[i]=min(t[j]+dp[i-j],dp[i]);
}
}
printf("%d\n",dp[n]);
}
return 0;
}
背包
#include
#include
#include
using namespace std;
void f(int n,int k,int c[],int w[],int m[])
{
int v[30005]={0};
int i,j,t;
for(i=1;i<=n;i++)
{
if(m[i]==233||c[i]*m[i]>k)
{
for(j=c[i];j<=k;j++)
{
v[j]=max(v[j],v[j-c[i]]+w[i]);
}
} //完全背包
else{
int num=m[i];
//不要忘记这个条件
for (t = 1; num > 0; t <<= 1) {
if (t > num) t = num;
num -= t;
for ( j = k; j >= c[i] * t; j--)
v[j] = max(v[j], v[j - c[i] * t] + w[i] * t);
}
} //01背包
}
printf("%d\n",v[k]);
}
int main()
{
int n,k;
while(~scanf("%d %d",&n,&k))
{
int c[505]={0};//????
int w[505]={0}; //????
int m[505]={0};
int i;
for(i=1;i<=n;i++)
{
scanf("%d %d %d",&c[i],&w[i],&m[i]);
}
f(n,k,c,w,m);
}
return 0;
}
矩阵链相乘–n个归并成一个
#include
#include
#include
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
int mintimes(int p[],int m[][305],int s[][305],int n)
{
int i,k,l;
for(i=1;i<=n;i++)
m[i][i]=0;
for(l=2;l<=n;l++) //矩阵链长度从2到n
{
for(i=1;i<=n+1-l;i++) //矩阵链开始位置
{
m[i][i+l-1]= INT_MAX;
for(k=i;k=m[i][k]+m[k+1][i+l-1]+p[i-1]*p[k]*p[i+l-1])
{
m[i][i+l-1]=m[i][k]+m[k+1][i+l-1]+p[i-1]*p[k]*p[i+l-1];
s[i][i+l-1]=k;
}
}
}
}
return m[1][n];
}
void print_method(int s[][305],int i,int j)
{
if(i==j)
{
printf("A%d",i);
return;
}
int k=s[i][j];
printf("(");
print_method(s,i,k);
print_method(s,k+1,j);
printf(")");
}
int main(int argc, char** argv) {
int n;
int p[305];
int m[305][305],s[305][305]; //m[i][j] 从第i个到第个j矩阵链的乘法次数
while(~scanf("%d",&n))
{
int i;
for(i=0;i<=n;i++)
scanf("%d",&p[i]);
int times = mintimes(p,m,s,n);
printf("%d\n",times);
print_method(s,1,n);
printf("\n");
}
return 0;
}
OBST
#include
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
const int maxn=500+5;
const int MAX = 2147483647;
int obst(int n,int p[],int q[])
{
int e[maxn][maxn]; //包含ki---kj关键字的搜索代价
int w[maxn][maxn]; //包含ki---kj关键字的出现次数
int i,j,r,len;
for(i=1;i<=n+1;i++)
{
e[i][i-1]=q[i-1];
w[i][i-1]=q[i-1];
}
/*for(i=1;i<=n;i++)
{
for(j=i;j<=n;j++)
{
w[i][j]=w[i][j-1]+p[j-1]+q[j-1];
}
}*/
for(len=1;len<=n;len++) //子树长度
{
for(j=1;j+len-1<=n;j++) //起点
{
int k=j+len-1;
w[j][k]=w[j][k-1]+p[k]+q[k];
int min=MAX; //注意min的位置,要恢复
for(r=j;r<=j+len-1;r++)
{ //根节点
if(e[j][r-1]+e[r+1][k]+w[j][k] 贪心算法
做出每个贪心选择后产生一个子问题。求表达式,交换两个选择,探寻最优选择。常用优先队列优化选择
活动选择问题
n个活动1个资源任意活动进行时唯一占用该资源
原则:最早结束,最早开始,最短时间
#include
#include
#include
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
const int maxn= 1000;
typedef pairp;
p act[maxn];
p choose[maxn];
/*struct cmp
{
bool operator ()(p &a,p &b)
{
return a.second>b.second;
}
};*/
bool cmp (p a,p b)
{
return a.second,cmp>que;
int main(int argc, char** argv) {
int n;
scanf("%d",&n);
int i;
for(i=1;i<=n;i++)
{
scanf("%d%d",&act[i].first,&act[i].second);
//que.push(act[i]);
}
/*int j=1;
choose[j++]=que.top();
que.pop();
while(!que.empty()){
if(que.top().first>=choose[j-1].second)
{
choose[j++]=que.top();
}
que.pop();
}
printf("%d",j-1);*/
sort(act,act+n,cmp);
int num=1,j;
i=1;
for(j=2;j<=n;j++)
{
if(act[j].first>act[i].second)//每次选取结束时间最早的活动
{
i=j;
num++;
printf("%d %d\n",i,act[i].second);
}
}
printf("%d",num);
return 0;
}
分数背包
#include
#include
#include
using namespace std;
const int maxn = 100000+7;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
struct trash
{
int ti;
int mi;
double fra;
} ;
trash a[maxn];
bool cmp(trash x, trash y)
{
return x.fra >y.fra ;
}
int main(int argc, char** argv) {
int n,t,i;
scanf("%d %d",&n,&t);
for(i=1;i<=n;i++){
scanf("%d%d",&a[i].ti,&a[i].mi );
a[i].fra =(double)a[i].mi/(double)a[i].ti; //注意精度转换
}
sort(a+1,a+n+1,cmp);
int num=t;
double ans=0;
for(i=1;i<=n&&num>0;i++)
{
if(num 最小生成树
#include
#include
#include
#include
#include
using namespace std;
const int maxn=2e5+10;
int pre[5010];
struct node
{
int u,v;
int value;
}p[maxn];
void init(int n)
{
for(int i=1;i<=n;i++)
{
pre[i]=i;
}
}
int find(int x)
{
if(pre[x]==x) return x;
return pre[x]=find(pre[x]);
}
bool cmp (node x,node y)
{
return x.value 动态规划
背包
#include
#include
#include
using namespace std;
void f(int n,int k,int c[],int w[],int m[])
{
int v[30005]={0};
int i,j,t;
for(i=1;i<=n;i++)
{
if(m[i]==233||c[i]*m[i]>k)
{
for(j=c[i];j<=k;j++)
{
v[j]=max(v[j],v[j-c[i]]+w[i]);
}
} //完全背包
else{
int num=m[i];
//不要忘记这个条件
for (t = 1; num > 0; t <<= 1) {
if (t > num) t = num;
num -= t;
for ( j = k; j >= c[i] * t; j--)
v[j] = max(v[j], v[j - c[i] * t] + w[i] * t);
}
} //01背包
}
printf("%d\n",v[k]);
}
int main()
{
int n,k;
while(~scanf("%d %d",&n,&k))
{
int c[505]={0};//????
int w[505]={0}; //????
int m[505]={0};
int i;
for(i=1;i<=n;i++)
{
scanf("%d %d %d",&c[i],&w[i],&m[i]);
}
f(n,k,c,w,m);
}
return 0;
}
图算法
dfs
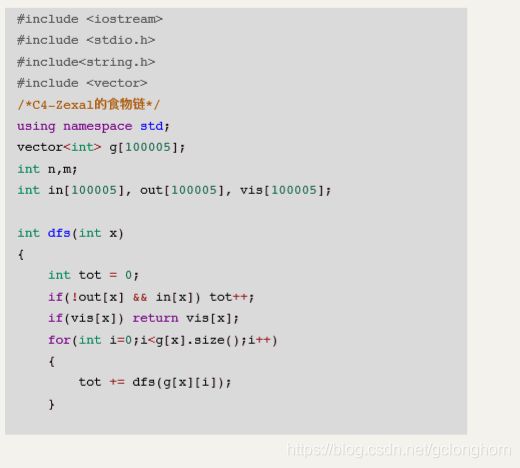
食物链数 基本路个数
dfs板子
int cnt=0;
void dfs(int start,int cnt)//start
{
int i;
if(check())
{
return;
}
for(i=start;i<=g;i++)
{
if(!marked[i])
{
marked[i]=true; //入栈
que.push_back(i);
dfs(i,cnt+1);
marked[i]=false; //出栈
que.pop_back();
}
}
}
bfs矩阵连通分量
#include
#include
#include
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
struct pp
{
int x,y;
};
dequeq;
bool map[105][105],marked[105][105];
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
int m,n;
int ans=0;
void bfs(int sx,int sy)//bfs
{
pp st;
st.x=sx;st.y=sy;
marked[sx][sy]=1;
q.push_back(st);
while(!q.empty())
{
pp nw=q.front();
for(int i=0;i<4;i++)
{
pp nxt=nw;
nxt.x+=dx[i];
nxt.y+=dy[i];
if(map[nxt.x][nxt.y]!=0 && marked[nxt.x][nxt.y]!=1)
{
marked[nxt.x][nxt.y]=1;//把这一连通块的点染色
q.push_back(nxt);}
}
q.pop_front();
}
}
int main(int argc, char** argv) {
cin>>m>>n;
int i,j;
char a;
memset(map,0,sizeof(map));
for(i=1;i<=m;i++)
{
for(j=1;j<=n;j++)
{
cin>>a;
map[i][j]=(a!='0');
}
}
for(i=1;i<=m;i++)
{
for(j=1;j<=n;j++)
{
if((!marked[i][j])&&(map[i][j]))
{
bfs(i,j);
ans++;
}
}
}
cout<
输出所有组合Cmn
#include
#include
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
vectorque;
bool marked[10];
int count;
void dfs(int i,int m,int n){
int j,k;
que.push_back(i);
count++;
marked[i]=true;
if(count spfa
单源最短路径
#include
#include
#include
#include
#include
#define inf 0x3f3f3f3f
#define maxn 200025
using namespace std;
struct wayy
{
int next,to,from,w;
}edge[maxn];
int head[maxn]={0};
int n,m,cnt=1;
int dist[maxn]={0},vis[maxn]={0};
struct node
{
int index,dist;
};
queue q;
void add(int u,int v,int w)
{
edge[cnt].w=w;
edge[cnt].to=v;
edge[cnt].from=u;
edge[cnt].next=head[u];
head[u]=cnt;
cnt++;
}
void spfa(int s,int to)
{
int i,j,v;
for(i=0;i<=n;i++)
{
dist[i]=inf;
vis[i]=false;
}
dist[s]=0;vis[s]=1;
q.push(s);
while(!q.empty())
{
v=q.front();
q.pop();
vis[v]=0;
for(j=head[v];j;j=edge[j].next)
{
int u =edge[j].to ;
if(dist[u]>dist[v]+edge[j].w)
{
dist[u]=dist[v]+edge[j].w;
if(!vis[u])
{
vis[u]=true;
q.push(u);
}
}
}
}
}
int main()
{
int i,j,x,y,w,s,t;
scanf("%d%d%d%d",&n,&m,&s,&t);
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&w);
add(x,y,w);
add(y,x,w);
}
spfa(s,t);
cout< spfa判断自环:入队次数大于入度。
floyd
非负权无环图 多源最短路径
#include
#include
#include
using namespace std;
const int maxn=200+7;
const int INF = 0x3f3f3f3f;
int e[maxn][maxn]; //保存图
int n,m;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
void floyd()
{
int i,j,k;
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(e[i][j]>e[i][k]+e[k][j])
{
e[i][j]=e[i][k]+e[k][j];
}
}
}
void findmax(){
int mx=0;
int i,j;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if (e[i][j] != INF) mx = max(e[i][j], mx);
}
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(e[i][j]==mx)
printf("%d %d\n",i,j);
}
}
/*
*/
int main(int argc, char** argv) {
int t;
scanf("%d",&t);
while(t--)
{
int a,b,c,i,j;
scanf(("%d%d"),&n,&m);
memset(e,INF,sizeof(e));
for(i=1;i<=n;i++)
e[i][i]=0;
while(m--)
{
scanf("%d%d%d",&a,&b,&c);
e[a][b]=c;
}
floyd();
findmax();
}
return 0;
}
最大流
ek算法
#include
#include
#include
#include
#include
using namespace std;
const int maxn=1007;
const int inf=0x7fffffff;
int r[maxn][maxn];
bool visit[maxn];
int pre[maxn];
int m,n;
//bfs?????,????ture
bool bfs(int s,int t){
queue q;
int p;
memset(visit,false,sizeof(visit));
memset(pre,-1,sizeof(pre));
pre[s]=s;
q.push(s);
visit[s]=true;
while(!q.empty()){
p=q.front();
q.pop();
//??????????1??,???????
for(int i=1;i<=n;++i){
if(r[p][i]>0&&!visit[i]){
visit[i]=true;
pre[i]=p;
if(i==t)
return true;
q.push(i);
}
}
}
return false;
}
int EK(int s,int t){
//inc???????????
int maxflow=0,inc;
while(bfs(s,t)){
//?:??????????inc?inf
inc=inf;
for(int i=t;i!=s;i=pre[i]){
if(inc>r[pre[i]][i]){
inc=r[pre[i]][i];
}
}
//????????????????r????0
for(int i=t;i!=s;i=pre[i]){
r[pre[i]][i]-=inc;
r[i][pre[i]]+=inc;
}
maxflow+=inc;
}
return maxflow;
}
void startEK(){
int a,b,c;
int ans;
scanf("%d%d",&n,&m);
memset(r,0,sizeof(r));
for(int i=0;i 二分图匹配匈牙利算法
#include
#include
#include
using namespace std;
const int MAX =10000+7;
int n;
int a[MAX][MAX],used[MAX],lover[MAX];//a男生暗恋对象, lover对象是谁
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
bool find(int x){
int j;
for(j=1;j<=n;j++)
{
if (!used[j]&&a[x][j])
{
used[j]=1; //试图改变女生的归属但失败了,其他男生在遇到女生就不折腾了
if(lover[j]==0||find(lover[j])) //名花无主或能腾出位置
{
lover[j]=x;
return true;
}
}
}
return false;
}
int main(int argc, char** argv) {
int i,x,y;
while(~scanf("%d",&n))
{
int x=0;//配对成功数
memset(a,0,sizeof(a));
memset(lover,0,sizeof(lover));
for(i=1;i<=n;i++)
{
scanf("%d",&y);
a[i][y]=a[y][i]=1;
}
for(i=1;i<=n;i++)
{
scanf("%d",&y);
a[y][i]=a[i][y]=1;
}
for(i=1;i<=n;i++)
{
memset(used,0,sizeof(used));
if(find(i))
x++;
}
printf("%d\n",n-x);
}
return 0;
}
计算几何
sqrt 平方根 sqr平方 atan反正切
凸包
#include
#include
#include
#include
#define eps 1e-12
using namespace std;
const double pi= acos(-1);
int cnt; //凸包点个数
struct point
{
double x,y;
point(double _x=0,double _y=0){x=_x;y=_y;};
}p[400010],s[400010];
bool operator <(const point&l,const point&r)
{
if(l.y==r.y)return l.x0) return length(v3);
return fabs(cross(v1,v2))/len(v1);
}
bool cmp(const point&p1,const point&p2)
{
double tmp=cross(p1-p[1],p2-p[1]);
if(tmp>0)return 1;
if(tmp==0&&dis(p[0],p1)1&&cross(s[cnt]-s[cnt-1],p[i]-s[cnt])<=0)cnt--;
cnt++;
s[cnt]=p[i];
}
s[cnt+1]=p[1];
}
int main(int argc, char** argv) {
int n,i,j;
cin>>n;
double a,b,R,X,Y,th;
cin>>a>>b>>R;
a-=R*2;//切掉后的边长
b-=R*2;
double Long=sqrt(a*a+b*b)/2;//算出对角线的一半
double An[4];//方便计算4个点的坐标
//这个公式就不一一说明了,自己总可以推出来QAQ
An[0]=atan(a/b);
An[1]=pi-An[0];
An[2]=pi+An[0];
An[3]=2*pi-An[0];
double ans=R*2*pi;//现在ans里放一个圆的周长
for(i=1;i<=n*4;i+=4)
{
cin>>X>>Y>>th;
for(j=0;j<4;j++)
{//把4个点加入点集
p[i+j].x=cos(th+An[j])*Long+X;
p[i+j].y=sin(th+An[j])*Long+Y;
}
}
n=n*4;
graham(n);
ans+=cir();
printf("%.2lf\n",ans);
return 0;
}
整数格点数
int gcd(int a,int b){return b==0?a:gcd(b,a%b);}//最大公约数
int s,b,i,n,m,p;
int main()
{
freopen("fence9.in","r",stdin);
freopen("fence9.out","w",stdout);
scanf("%d%d%d",&n,&m,&p);
b=gcd(n,m)+gcd(abs(p-n),m)+p;//边上格点数目
s=(p*m)/2;//面积 s=i+b/2-1
i=s-b/2+1;
printf("%d\n",i);
return 0;
}
fft 大数乘法
#include
#include
#include
#include
#include
#include
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
const double pi = acos (-1.0);
struct complex
{
double x,y;
complex(double xx=0.0,double yy=0.0)
{
x=xx;
y=yy;
}
complex operator -(const complex &b)const
{
return complex(x-b.x,y-b.y);
}
complex operator +(const complex &b)const
{
return complex(x+b.x,y+b.y);
}
complex operator *(const complex &b)const
{
return complex(x*b.x-y*b.y,x*b.y+y*b.x);
}
};
void change(complex y[],int len)
{
int i,j,k;
for(i=1,j=len/2;i=k)
{
j-=k;
k/=2;
}
if(j>str1>>str2){
int i,f1=1,f2=1;
if(str1[0]=='-')
{
f1=-1;
str1.erase(0,1);
}
if(str2[0]=='-')
{
f2=-1;
str2.erase(0,1);
}
int len1= str1.length();
int len2 = str2.length();
int len=1;
while(len0)len--;
if(f1*f2==-1&&str1[0]!='0'&&str2[0]!='0')printf("-");
for(int i=len;i>=0;i--)
printf("%c",sum[i]+'0');
printf("\n");
}
return 0;
}
#include
#include
#include
#include
#include
#include
#define PI acos(-1)
using namespace std;
typedef long long ll;
const int MAXN = 1e6+5;
struct complex {
double a, b;
complex(double aa = 0.0, double bb = 0.0) { a = aa; b = bb; }
complex operator +(const complex &e) { return complex(a + e.a, b + e.b); }
complex operator -(const complex &e) { return complex(a - e.a, b - e.b); }
complex operator *(const complex &e) { return complex(a * e.a - b * e.b, a * e.b + b * e.a); }
}x1[MAXN], x2[MAXN], x[MAXN];
void change(complex *y, int len){
int i, j, k;
for(i=1,j=len/2; i= k){ j-=k; k>>=1; }
if(j < k) j += k;
}
}
void fft(complex *y, int len, int on){
change(y, len);
for(int h=2; h<=len; h<<=1){
complex wn(cos(-on*2*PI/h), sin(-on*2*PI/h));
for(int j=0; j while(T--){
scanf("%d",&n);
memset(num,0,sizeof(num));
for(int i = 0;i < n;i++){
scanf("%d",&a[i]);
num[a[i]]++;
}
sort(a,a+n);
int len1 = a[n-1]+1;
int len = 1;
while( len < 2*len1 )len <<= 1;
for(int i = 0;i < len1;i++)
x1[i] = Complex(num[i],0);
for(int i = len1;i < len;i++)
x1[i] = Complex(0,0);
fft(x1,len,1);
for(int i = 0;i < len;i++)
x1[i] = x1[i]*x1[i];
fft(x1,len,-1);
for(int i = 0;i < len;i++)
num[i] = (long long)(x1[i].r+0.5);
len = 2*a[n-1];//为105行代码的处理优化一下界
for(int i = 0;i < n;i++) {num[a[i]+a[i]]--;} //减掉取两个相同的组合
for(int i = 1;i <= len;i++) {num[i]/=2;} //选择的无序,除以2
sum[0] = 0;
for(int i = 1;i <= len;i++){sum[i] = sum[i-1]+num[i];}//卷积的前缀和
long long cnt = 0;//能够组成三角形的个数
for(int i = 0;i < n;i++){
cnt += sum[len]-sum[a[i]];
cnt -= (long long)(n-1-i)*i; //减掉一个取大,一个取小的
cnt -= (n-1); //减掉一个取本身,另外一个取其它
cnt -= (long long)(n-1-i)*(n-i-2)/2;//减掉大于它的取两个的组合
}
//总数
long long tot = (long long)n*(n-1)*(n-2)/6;//答案概率的分母C(n , 3)
printf("%.7lf\n",(double)cnt/tot);
}
return 0;
}
kmp
#include
#include
#include
using namespace std;
const int maxn = 1e6+10;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
void cal_next(char *str, int *next, int len)
{
next[1] = 0;//next[1]初始化为0,0表示不存在相同的最大前缀和最大后缀
int k = 0;//k初始化为0
for (int q = 2; q <= len; q++)
{
while (k > 0 && str[k + 1] != str[q])//如果下一个不同,那么k就变成next[k],注意next[k]是小于k的,无论k取任何值。
{
k = next[k];//往前回溯
}
if (str[k + 1] == str[q])//如果相同,k++
{
k = k + 1;
}
next[q] = k;//这个是把算的k的值(就是相同的最大前缀和最大后缀长)赋给next[q]
}
}
void KMP(char *str, int slen, char *ptr, int plen,int *next)
{
cal_next(ptr, next, plen);//计算next数组
int k = 0;
for (int i = 1; i <= slen; i++)
{
while (k >0&& ptr[k + 1] != str[i])//ptr和str不匹配,且k>0(表示ptr和str有部分匹配)
k = next[k];//往前回溯
if (ptr[k + 1] == str[i])
k = k + 1;
if (k == plen)//说明k移动到ptr的最末端
{
cout << i-plen+1<< endl;
k = 0;//重新初始化,寻找下一个
i = i - plen + 1;//i定位到该位置,外层for循环i++可以继续找下一个(这里默认存在两个匹配字符串可以部分重叠),感谢评论中同学指出错误。
}
}
}
int main()
{
char str[maxn],ptr[maxn];
cin>>str+1>>ptr+1;
int slen,plen;
slen=strlen(str+1);
plen=strlen(ptr+1);
int *next= new int[plen];
KMP(str,slen,ptr,plen,next);
int i;
for(i=1;i<=plen;i++)cout< 习惯性错误
1.注意循环中循环条件,变量的更新
2.int double 混合运算的精度问题
3.min函数一次性只能比较两个数
4.
取模的时候每次都要取模 今后取模都请使用形如"(a+mod)%mod"的形式来代替"a%mod"
int ans=(a[r]-a[l-1]+mod)%mod; 防止出现复数
5.memset 只能设0 不能设其他值
输入
多行不定长输入
char str[maxn],ptr[maxn];
cin>>str+1>>ptr+1;
int slen,plen;
slen=strlen(str+1);
plen=strlen(ptr+1);
贪心用了冒泡排序
for(i=1;i<=n;i++)
{
for(j=1;j<=n-i;j++)
{
if(a[j].t *a[j+1].d >a[j+1].t *a[j].d )
{
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}