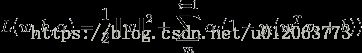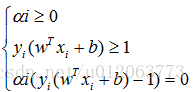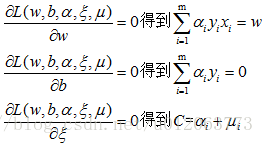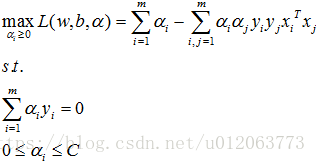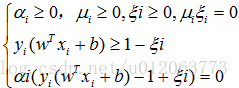SVM总结
第一部分:线性可分
目标:对于给定的样本集![]() ,想办法使用一条线(二维)或者超平面将不同类别的样本尽可能分开。划分超平面具有最强的鲁棒性。
,想办法使用一条线(二维)或者超平面将不同类别的样本尽可能分开。划分超平面具有最强的鲁棒性。
即:以二分类为例,目标是找到 距离最近的两类样本点距离最远的分割面。
样本空间中,划分超平面:![]() ,该超平面可被w和b确定。
,该超平面可被w和b确定。
其中: ![]() ,是法向量,决定超平面的方向;b是位移项,决定了超平面和原点间的距离。
,是法向量,决定超平面的方向;b是位移项,决定了超平面和原点间的距离。
2、若能分类正确,表示对于![]()
支持向量机去求解二类问题,目标是求一个特征空间的超平面,而超平面分开的两类对应于超平面的函数值的符号是刚好相反的
一个平面正确分类样本数据,就相当于用这个平面计算的那个y*f(x)>0
svm中y取1或-1的历史原因是因为感知器最初的定义,实际取值可以任意,总能明确表示输入样本是否被误分,但是用+1、-1可以起码可以是问题描述简单化、式子表示简洁化、几何意义明确化。 举个例子,如你要是取y为1和2,比如原来取-1的现在取1,原来取1的现在取2 , 这样一来,分类正确的判定标准变为(y-1.5)*f(X)>0 ,
故取1和-1只是为了计算简单方便,没有实质变化,更非一定必须取一正一负。
由于该式子是一个有不等式约束的凸二次优化问题,所以,直接求解不好求,转换成对偶问题。利用拉格朗日乘子法,可以得到该问题的拉格朗日函数:
(1)式为:![]() ------A
------A
若想要A==B(等价于B),即:
用(2)式对w,b分别求偏导数,得到:
带入(2)中,得到:
KKT条件的意义:它是一个非线性规划(Nonlinear Programming)问题能有最优化解法的必要和充分条件
由于,以上过程满足KKT条件,
所以,该问题有最优解:
第二部分:线性不可分
原始空间是有限维,即可通过核函数映射到高维线性可分空间。
![]() 表示将x映射到高维空间的特征向量,在特征空间中划分超平面所对应的模型可以表示为:
表示将x映射到高维空间的特征向量,在特征空间中划分超平面所对应的模型可以表示为:
![]()
类似上面(1)式,目标函数是:
其对偶问题是:
![]() 是样本xi和xj在高维特征空间的内积,设想有个函数,即核函数。可以满足xi和xj在高维特征空间的内积等于他们在原始空间内通过k(.,.)计算得结果:
是样本xi和xj在高维特征空间的内积,设想有个函数,即核函数。可以满足xi和xj在高维特征空间的内积等于他们在原始空间内通过k(.,.)计算得结果:
![]()
所以,(4)式可以转换成:
KKT条件同前面,得到:
核函数:1)线性核函数2)高斯核函数3)多项式核函数4)拉普拉斯核函数5)Sigmoid核函数
如何选择合适的核函数?
1.当样本的特征很多,即特征的维数很高,这是往往样本线性可分,可考虑用线性核函数的SVM或LR(如果不考虑核函数,LR和SVM都是线性分类算法,也就是说他们的分类决策面都是线性的)。
2.当样本的数量很多,但特征较少时,可以手动添加一些特征,使样本线性可分,再考虑用线性核函数的SVM或LR。
3.当样本特征维度不高时,样本数量也不多时,考虑用高斯核函数
(RBF核函数的一种,指数核函数和拉普拉斯核函数也属于RBF核函数)。
通常采用的方法有:
一是利用专家的先验知识预先选定核函数;
二是采用Cross-Validation方法,即在进行核函数选取时,分别试用不同的核函数,归纳误差最小的核函数就是最好的核函数.如针对傅立叶核、RBF核,结合信号处理问题中的函数回归问题,通过仿真实验,对比分析了在相同数据条件下,采用傅立叶核的SVM要比采用RBF核的SVM误差小很多.
三是采用由Smits等人提出的混合核函数方法,该方法较之前两者是目前选取核函数的主流方法,也是关于如何构造核函数的又一开创性的工作.将不同的核函数结合起来后会有更好的特性,这是混合核函数方法的基本思想.
第三部分:近似线性可分
软间隔:最大化间隔的同时,允许部分点不满足,当然,这种情况尽可能少。采用hinge损失函数,得到优化目标为:
备注,其他类型的替代损失函数:
A:hinge损失函数:l(z)=max(0,1-z):可以保持稀疏性,只与支持向量有关
B:指数损失函数:lex(z)=exp(-z)
C:对率损失函数:llog(z)=log(1+exp(-z)):输出具有自然的概率意义,能直接用于多分类任务
D:平方损失函数
E:绝对值损失函数
F:0-1损失函数:非凸、非连续、数学性质不太好,不易求解,通常采用A-C三种损失函数
得到对偶问题:
以上满足KKT条件为:
所以该问题有最优解:
第四部分:SVM(支持向量机)和softmax的区别

第五部分:LR和SVM的联系和区别
联系:
1、LR和SVM都可以处理分类问题,且一般都用于处理线性二分类问题(在改进的情况下可以处理多分类问题)
2、两个方法都可以增加不同的正则化项,如l1、l2等等。所以在很多实验中,两种算法的结果是很接近的。
3、LR和SVM都可以用来做非线性分类,只要加核函数就好。
4、LR和SVM都是线性模型,当然这里我们不要考虑核函数
5、都属于判别模型
区别:
1、LR是参数模型,SVM是非参数模型。
2、从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
3、逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
4、SVM不直接依赖数据分布,而LR则依赖,因为SVM只与支持向量那几个点有关系,而LR和所有点都有关系。
5、SVM依赖penalty系数,实验中需要做CV
6、SVM本身是结构风险最小化模型,而LR是经验风险最小化模型