二叉树面试题

1.创建一颗二叉树

template<class T>
struct BinaryTreeNode
{
    BinaryTreeNode(const T& data)
    :_left(NULL)
    , _right(NULL)
    , _data(data)
    {}
    BinaryTreeNode* _left;
    BinaryTreeNode* _right;
    T _data;
};
void CreateBinaryTree(Node*& pRoot, const T* array, size_t size, size_t& index,const T& invalid)
    {
        if (index < size && array[index]!=invalid)
        {
            pRoot = new Node(array[index]);
            //创建pRoot的左子树
                CreateBinaryTree(pRoot->_left, array, size, ++index,invalid);
            //创建pRoot的右子树
                CreateBinaryTree(pRoot->_right, array, size, ++index,invalid);
        }
    }

2.前/中/后序遍历二叉树（递归）
（1）前序（遍历次序：根节点->左子树->右子树）

void _PreOrder(Node* pRoot)
    {
        if (pRoot)
        {
            cout << pRoot-> _data <<" ";
            _PreOrder(pRoot->_left);
            _PreOrder(pRoot->_right);
        }
    }

（2）中序（遍历次序：左子树->根节点->右子树）

void _InOrder(Node* pRoot)
    {
        if (pRoot)
        {
            _InOrder(pRoot->_left);
            cout << pRoot->_data << " ";
            _InOrder(pRoot->_right);
        }
    }

（3）后序（遍历次序：左子树->右子树->根节点）

void _PostOrder(Node* pRoot)
    {
        if (pRoot)
        {
            _PostOrder(pRoot->_left);
            _PostOrder(pRoot->_right);
            cout << pRoot->_data << " ";
        }
    }

3.前/中/后序遍历二叉树（非递归）

void _PreOrder_Nor(Node* pRoot)  //前序遍历非递归
    {
        stack s;
        Node* pcur = pRoot;
        while (pcur || !s.empty())
        {
            while (pcur)
            {
                //访问根节点，根结点入栈
                cout << pcur->_data << " ";
                s.push(pcur);
                pcur = pcur->_left;
            }
            pcur = s.top();
            s.pop();
            //若pcur右子树存在，将其当成一颗新的树来访问
            pcur = pcur->_right;
        }
    }

void _InOrder_Nor(Node* pRoot)   //中序遍历非递归
    {
        stack s;
        Node* pcur = pRoot;
        while (pcur || !s.empty())
        { //找最左边的结点，并保存路径上经过的所有节点
            while (pcur)
            {
                s.push(pcur);  //根结点入栈
                pcur = pcur->_left;
            }
            //取栈顶元素并访问
            pcur = s.top();
            cout << pcur->_data << " ";
            s.pop();
            //若pcur右子树存在，将其当成一颗新的树来访问
            pcur = pcur->_right;
        }

void _PostOrder_Nor(Node* pRoot)   //后序遍历非递归
    {
        stack s;
        Node* prev = NULL;  //标记最近刚访问过的结点
        Node* pcur = pRoot;
        while (pcur || !s.empty())
        { //找最左边的结点，并保存路径上经过的所有节点
            while (pcur)
            {
                s.push(pcur);  //根结点入栈
                pcur = pcur->_left;
            }
            // 取栈顶元素并访问
            pcur = s.top();
            if (pcur->_right == NULL || pcur->_right == prev)
            {
                cout << pcur->_data << " ";
                prev = pcur;
                s.pop();
                pcur = NULL;
            }
            else
            {
                pcur = pcur->_right;
            }
        }
    }

4.层序遍历二叉树

void _LevelOrder_Nor(Node* pRoot) //层序遍历
    {
        //1 每一次打印一个结点，如果该节点有子结点，则把该结点的子结点放到一个队列的末尾
        //2 接下来到队列的头部取出最早进入队列的结点，打印，直到队列中所有的结点都被打印出来
        if (pRoot == NULL)
            return;
        deque q;  //定义一个队列
        q.push_back(pRoot);  //根节点入队列
        while (q.size())   //判满
        {
            Node* pNode = q.front();  //取队头元素
            q.pop_front();
            cout << pNode->_data << " ";
            if (pNode->_left)
            q.push_back(pNode->_left);  //左子树入队列
            if (pNode->_right)
            q.push_back(pNode->_right);  //右子树入队列
        }
    }

5.求二叉树的高度

size_t _Height(Node* pRoot)  //求二叉树的深度
    {
        if (pRoot == NULL)
            return 0;
        if (pRoot->_left == NULL && pRoot->_right == NULL)
            return 1;
        size_t leftHeight = _Height(pRoot->_left);
        size_t rightHeight = _Height(pRoot->_right);
        return (leftHeight > rightHeight) ? leftHeight + 1 : rightHeight + 1;
    }

6.求叶子结点的个数（度为0的结点的个数）

    size_t _GetLeefCount(Node* pRoot)  //求二叉树叶子结点的个数
    {
        if (pRoot == NULL)
            return 0;
        if (pRoot->_left == NULL&&pRoot->_right == NULL)
            return 1;
        return _GetLeefCount(pRoot->_left) + _GetLeefCount(pRoot->_right);

7.判断一个结点是否在一棵二叉树中

Node* _Find(Node* pRoot,  const T& data)
    {
        if (pRoot == NULL)
            return NULL;
        if (pRoot->_data == data)
            return pRoot;
        Node* ret = NULL;
        if (ret = _Find(pRoot->_left, data))
            return ret;
            return  _Find(pRoot->_right, data);
    }

8.获取指定结点的双亲结点

Node* _GetParent(Node* pRoot,Node* pNode) //求一个结点的双亲结点
    {
        if (pRoot==NULL||(pRoot->_left == NULL&&pRoot->_right == NULL))
            return NULL;
        if (pRoot->_left == pNode || pRoot->_right == pNode)
            return pRoot;
        Node* ret = NULL;
        if (ret =_GetParent(pRoot->_left, pNode))  //不为空就返回
            return ret;
            return _GetParent(pRoot->_right, pNode);
    }

9.求二叉树的镜像

void _MirrorBinaryTree(Node* pRoot) //求二叉树的镜像
    {
        //1 先序遍历二叉树的每一个结点
        //2 如果遍历到的结点有子结点，就交换它的两个子结点，直到交换完所有非叶子结点的左右子结点
        if (pRoot == NULL)
            return;
        if (pRoot->_left == NULL&&pRoot->_right == NULL)
            return;
        Node* tmp = pRoot->_left;
        pRoot->_left = pRoot->_right;
        pRoot->_right = tmp;
        if (pRoot->_left)
            _MirrorBinaryTree(pRoot->_left);
        if (pRoot->_right)
            _MirrorBinaryTree(pRoot->_right);
    }

10.获取二叉树中第K层结点的个数

size_t _GetKLevelNodeCount(Node* pRoot, int K)
    {
        //若二叉树为空或者k小于0，返回0
        if (pRoot == NULL || K < 0)
            return 0;
        if (K == 1)  //只有一个根节点
            return 1;
        return _GetKLevelNodeCount(pRoot->_left, K - 1) + _GetKLevelNodeCount(pRoot->_right, K - 1);
    }

11.判断一棵二叉树是否是完全二叉树

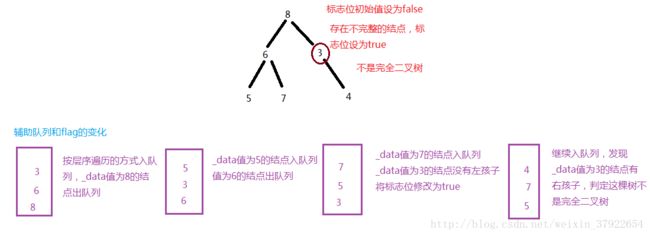
bool _IsCompleteBinaryTree(Node* pRoot)
    {
        bool flag = false;
        queue<Node*> q;
        q.push(pRoot);
        Node* pNode = q.front();
        while (pNode)
        {
            //有右孩子无左孩子
            if (pNode->_left == NULL && pNode->_right != NULL)
                return false;
            //如果flag=true并且当前节点存在孩子
            if (flag == true && (pNode->_left || pNode->_right))
                return false;
            //如果当前结点少一个孩子
            if (pNode->_left == NULL || pNode->_right == NULL)
                flag = true;
            if (pNode->_left)
                q.push(pNode->_left);
            if (pNode->_right)
                q.push(pNode->_right);
            q.pop();
            if (!q.empty())
                pNode = q.front();
            else
            pNode = NULL;
        }
        return true;
    }