TensorFlow Lite 采坑记(二):Model quantization 模型量化
TensorFlow Lite 从入门到
放弃
精通
-
- 前言
- 为什么要做模型量化
- 1. 量化原理
- 2. 模型量化加速原理
- 3. 两种方法
- 4. limitations
- 5. Quantization model 和 Float model 比较(数据请求中)
前言
从2012年AlexNet夺得当年ImageNet冠军开始,深度学习就开始呈爆破式发展,这个过程中迭代出很多优秀的深度学习代码框架,随着技术逐渐成熟,工业界对技术落地的需求越来越迫切,本文以TensorFlow为例,探究模型量化的相关原理和方法。
为什么要做模型量化
深度学习已被证明在包括图像分类(Image Classification),目标检测(Object Detection),自然语言处理(Natural Language Processing)等任务上效果很好。但到了实践中,模型的复杂程度度往往限制了其在各种现实应用场景下的部署。
图一:模型 MAC和网络预测准确度。
自 AlexNet 伊始,基于 ImageNet 的深度学习算法(或模型)改进都和模型大小相关。在如上的由 Google 研究人员给出的 图一 中,垂直方向是网络在给定任务上的效果,横向是网络的大小。通过对比图中 AlexNet,GoogleNet 和 VGG 的趋势不难看出,当模型变大时网络的准确度可能更高。
随着模型预测越来越准确,网络越来越深,神经网络消耗的内存大小成为问题(见下图),尤其是在移动设备上。通常情况下,目前(2019年初)的手机一般配备 4GB 内存来支持多个应用程序的同时运行。而三个模型运行一次通常就要占用1GB内存。
模型大小不仅是内存容量问题,也是内存带宽问题。模型在每次预测时都会使用模型的权重,图像相关的应用程序通常需要实时处理数据,这意味着至少 30 FPS。因此,如果部署相对较大的 ResNet-50 网络来分类,运行网络模型就需要 3GB/s 的内存带宽。网络运行时,内存、CPU 和电池会都在飞速消耗。
1. 量化原理
总的来说, 量化桥接了浮点和定点,使模型大幅度压缩同时使精度损失保持在合理范围内,减小了带宽需求。值得一提的是,量化后的模型在做inference的时候还是会将权重转换为浮点数。原理参考文献:Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
以下是基于该文献对量化的一些理解。
1.1 Quantization Scheme
定义 r r r为浮点类型的实际值, 定义 q q q为整型的量化值,量化模式可以简述为:
q = r S + Z q={r\over S } + Z q=Sr+Z
反之:
r = S ( q − Z ) r = S {(q - Z)} r=S(q−Z)
其中 S = r m a x − r m i n q m a x − q m i n S = {r{_{max}} - r{_{min}}\over q{_{max}} - q{_{min}}} S=qmax−qminrmax−rmin
Z = q m a x − r m a x ÷ S Z = q{_{max}} - r{_{max}} \div S Z=qmax−rmax÷S
这里的 S S S 和 Z Z Z 均为量化参数,前者如字面意思所示, Z Z Z 表示浮点数的 0 量化后对应的整型值,由于 0 在神经网络中有着特殊的含义(padding等),故必须有精确的整型值对应 0。对于量化后的值 q q q,通过量化参数 ( S , Z ) (S,Z) (S,Z) 可恢复到所代表的浮点数值。
假设使用8bit量化,量化后的整型值应该在[0,255]之间,对应的可以表示的浮点数值范围:
m i n = S ( 0 − Z ) min = S{(0-Z)} min=S(0−Z)
m a x = S ( 255 − Z ) max = S{(255 - Z)} max=S(255−Z)
对于超出[min, max]范围的浮点数值,量化后必须做截断。对于网络的每一层(或者每个input array),都会有不同的min、max,因为是由不同的量化参数 S S S, Z Z Z决定的。在[min, max]范围的浮点数经过量化后可以得到uint8的8bit整数。
1.2 Integer-arithmetic-only matrix multiplication
解决了数值的量化,接下来就是计算层面的问题。因为直观上来看量化是将权重和神经网络中的数据流从float转换成了uint,但在同时需要控制在计算时的精度损失在一个合理范围内,否则量化将毫无意义。可以预见的是,在整个神经网络的计算过程中矩阵乘法占了相当大的比重。
考虑两个 N N Nx N N N矩阵 r 1 r_{1} r1和 r 2 r_{2} r2的乘法,假设 r 3 r_{3} r3 = r 1 r_{1} r1 r 2 r_{2} r2,进行INT8量化。 易知:
r a ( i , j ) = S a ( q a ( i , j ) − Z a ) r{_a^{(i,j)}} = S{_a}{(q{_a^{(i,j)}-Z{_a}})} ra(i,j)=Sa(qa(i,j)−Za)
矩阵乘法可改写为:
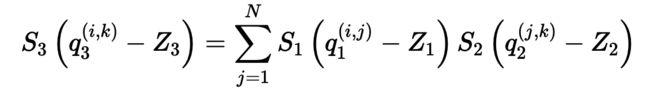
移项:

where M = S 1 S 2 S 3 = M 0 2 n M = {S{_1}S{_2}\over S{_3}} = {M{_0}\over 2{^n}} M=S3S1S2=2nM0
易知式中 M M M为FP32,其他均为INT8。实际上两个INT8之间的算术会累加到INT16或INT32,即超出INT8值域,但 Z 1 − 3 Z{_{1-3}} Z1−3项会使大多数的计算结果落入INT8值域中。
除乘法外,还有量化加法、减法、除法和指数等等运算。采用这些方法,量化神经网络可以在保证精度的同时大大减小模型大小和所需带宽。
2. 模型量化加速原理
上节探究了量化使模型大小大幅度下降并保持了一定的准确性,其实理论上来说,量化后的模型在CPU上的计算速度也会得到提升。
2.1 CPU命中率与L1 Cache
http://cpu.zol.com.cn/31/311395_all.html
2.2 im2col 与 Gemm
https://jackwish.net/gemm-optimization-and-convolution.html
https://petewarden.com/2015/04/20/why-gemm-is-at-the-heart-of-deep-learning/
相信读完这几篇文章就会对其有一定理解了。
3. 两种方法
3.1 Post-training quantization
官方文档提供了其python API和相关例子,详见:https://www.tensorflow.org/lite/performance/post_training_quantization
3.2 Quantization-aware training
TensorFlow 在支持训练后量化的同时还引入了训练时量化 Quantization-aware Training https://github.com/tensorflow/tensorflow/tree/r1.13/tensorflow/contrib/quantize ,其中包括四个步骤:
- 用常规方法训练一个 TensorFlow 浮点模型。
- 用
tf.contrib.quantize重写网络以插入Fake-Quant 节点并训练 min/max。 - 用 TensorFlow Lite 工具量化网络(该工具读取步骤 2 训练的 min/max)
- 用 TensorFlow Lite 部署量化的网络。
步骤 2 即所谓的量化感知训练(Quantization-aware Training),其中网络的前向(forward)模拟 INT8 计算,反向(backward)仍然是 FP32 。下图左半部分是量化网络,它接收 INT8 输入和权重并生成 INT8 输出。图十二右半部分是步骤 2 重写的网络,其中 Fake-Quant 节点(粉色)在训练期间将 FP32 张量量化为 INT8 (严格来讲仍然是经过 Quantize/Dequantize 过程的 FP32)
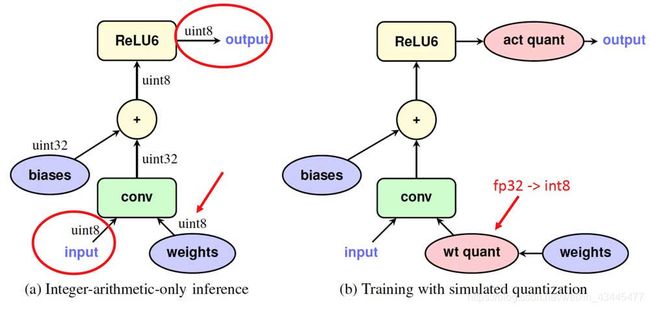
细节请参考论文Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
3.3 流程图
流程图是基于TensorFlow Lite官方文档整理,笔者分别尝试了Convert a TensorFlow GraphDef for quantized inference(命令行)和 post-training quantization两种方法。
官方文档链接:
Convert a TensorFlow GraphDef for quantized inference:
https://www.tensorflow.org/lite/convert/cmdline_examples#convert_a_tensorflow_graphdef_for_quantized_inference_
“dummy-quantization”:
https://www.tensorflow.org/lite/convert/cmdline_examples#use_dummy-quantization_to_try_out_quantized_inference_on_a_float_graph_
post-training quantization:
https://www.tensorflow.org/lite/performance/post_training_quantization
quantization-aware training:
https://github.com/tensorflow/tensorflow/tree/r1.13/tensorflow/contrib/quantize
4. limitations
主要有两点:
- 量化后的模型暂不支持GPU或NNAPI加速。
- 对于不同的CPU架构,其表现可能有较大差别(待验证)。
5. Quantization model 和 Float model 比较(数据请求中)
Reference:
https://jackwish.net/neural-network-quantization-introduction-chn.html
https://sf-zhou.github.io/ml/tensorflow_lite_and_uint8_quantization.html
https://zhuanlan.zhihu.com/p/42811261