TransE算法详解
TransE 算法详解
文章目录
- TransE 算法详解
- 算法背景
- 知识图谱是什么
- 知识表示是什么
- 基本思想
- 算法描述
- 梯度
- 参考文献
算法背景
知识图谱是什么
一条知识图谱可以表示为一个三元组(sub,rel,obj)。举个例子:小明的爸爸是大明,表示成三元组是(小明,爸爸,大明)。前者是主体,中间是关系,后者是客体。主体和客体统称为实体(entity)。关系有一个属性,不可逆,也就是说主体和客体不能颠倒过来。
知识图谱的集合,链接起来成为一个图(graph),每个节点是一个一个实体,每条边是一个关系,或者说是一个事实(fact)。也就是有向图,主体指向客体。
三元组的一个例子是
(姚明,出生于,上海)
(姚明,职业, 篮球运动员)
(姚明,性别,男)
为了简化起见,我们使用(h,r,t)来表示三元组。其中:
- h表示头实体
- r表示关系
- t表示尾实体
知识表示是什么
知识表示 实际上是让知识图谱的实体和关系向量化
具体的说,我们的目标是将知识库中所有的实体、关系表示成一个低纬度的向量。即 ( h , r , t ) → ( h ⃗ , r ⃗ , t ⃗ ) (h,r,t) \rightarrow (\vec h,\vec r,\vec t) (h,r,t)→(h,r,t)
这样的话,姚明就不是一个符号了,而是一个低维度的稠密的向量,例如:
[0.01, 0.04, 0.8, 0.32, 0.09, 0.18]
上面的向量取了6维,实际情况中的维度一般会比这个大, 大概在50~200左右。
在知识表示的大概念中,这种向量一般有一个专门的名称:embedding。
基本思想
算法描述
TransE算法认为,一个正确的三元组的embedding(h,r,t)会满足 h ⃗ + r ⃗ = t ⃗ \vec h + \vec r = \vec t h+r=t
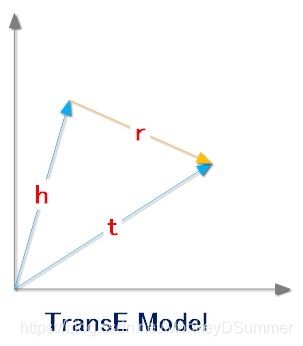
也就是说,头实体embedding加上关系embedding会等于尾实体embedding。同理,如果是一个错误的三元组,那么它们的embedding之间就不满足这种关系。
于是我们认为定义一个距离 d ( x ⃗ , y ⃗ ) d(\vec x , \vec y) d(x,y)来表示两个向量之间的距离,一般情况下,我们会取L1,或者L2 normal 。那么我们需要的是对一个正确的三元组 ( h , r , t ) (h, r, t) (h,r,t)来说,其距离 d ( h ⃗ + r ⃗ , t ⃗ ) d(\vec h + \vec r , \vec t) d(h+r,t)越小越好,相反对于一个错误的三元组 ( h ′ , r , t ′ ) (h', r, t') (h′,r,t′)来说距离 d ( h ′ ⃗ + r ⃗ , t ′ ⃗ ) d(\vec {h'} + \vec r , \vec {t'}) d(h′+r,t′)越大越好,因此给出目标函数:
min ∑ ( h , r , t ) ∈ S ∑ ( h ′ , r , t ′ ) ∈ S ′ [ γ + d ( h + r , t ) − d ( h ′ + r , t ′ ) ] + \min {\sum _ {(h,r,t) \in S} \sum _{(h', r, t') \in S'} [\gamma + d(h + r, t) - d(h' + r , t')]_+} min(h,r,t)∈S∑(h′,r,t′)∈S′∑[γ+d(h+r,t)−d(h′+r,t′)]+
其中
- Δ \Delta Δ 表示正确的三元组集合
- Δ ′ \Delta ' Δ′ 表示错误的三元组集合
- γ \gamma γ 表示正负样本之间的间距, 是一个常数
- [ x ] + [x]_+ [x]+ 表示 max ( 0 , x ) \max(0,x) max(0,x)
通常为了方便训练并避免过拟合,会加上约束条件
∣ ∣ h ∣ ∣ ≤ 1 , ∣ ∣ r ∣ ∣ ≤ 1 , ∣ ∣ t ∣ ∣ ≤ 1 , ||h|| \leq 1, ||r|| \leq 1, ||t|| \leq 1, ∣∣h∣∣≤1,∣∣r∣∣≤1,∣∣t∣∣≤1,
论文中的算法描述
梯度
以L2 normal 为例,梯度的计算相对比较简单,目标函数变为
l o s s = ∑ ( h , r , t ) ∈ S ∑ ( h ′ , r , t ′ ) ∈ S ′ [ γ + ( h + r − t ) 2 − ( h ′ + r − t ′ ) 2 ] + loss = {\sum _ {(h,r,t) \in S} \sum _{(h', r, t') \in S'} [\gamma + (h + r - t)^2 - (h' + r - t')^2]_+} loss=(h,r,t)∈S∑(h′,r,t′)∈S′∑[γ+(h+r−t)2−(h′+r−t′)2]+
举例来说,对某一个正确关系组中的头元素的参数 h i h_i hi来说 ∂ l o s s ∂ h i = ∑ ( h i , r , t ) ∈ S ∑ ( h ′ , r , t ′ ) ∈ S ′ ∂ [ γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 ] + ∂ h i \frac{\partial loss}{\partial h_i} = \sum_{(h_i,r,t)\in S} \sum _{(h', r, t') \in S'}\frac{\partial [\gamma + (h_i + r - t)^2 - (h' + r - t')^2]_+}{\partial h_i} ∂hi∂loss=(hi,r,t)∈S∑(h′,r,t′)∈S′∑∂hi∂[γ+(hi+r−t)2−(h′+r−t′)2]+
而 ∂ [ γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 ] + ∂ h i = { 2 ( h i + r − t ) γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 > 0 0 γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 < 0 \frac{\partial [\gamma + (h_i + r - t)^2 - (h' + r - t')^2]_+}{\partial h_i}= \begin{cases} 2(h_i + r - t) & \gamma + (h_i + r - t)^2 - (h' + r - t')^2 > 0\\ 0 & \gamma + (h_i + r - t)^2 - (h' + r - t')^2 < 0 \end{cases} ∂hi∂[γ+(hi+r−t)2−(h′+r−t′)2]+={2(hi+r−t)0γ+(hi+r−t)2−(h′+r−t′)2>0γ+(hi+r−t)2−(h′+r−t′)2<0
其他参数的偏导求解方式与 h i h_i hi的求导方式差异不大,这里不再赘述。
参考文献
https://xiangrongzeng.github.io/knowledge graph/transE.html
http://www.voidcn.com/article/p-wpxtiwou-cz.html
Bordes A, Usunier N, Garcia-Duran A, et al. Translating embeddings for modeling multi-relational data[C]//Advances in neural information processing systems. 2013: 2787-2795.
